Title Description (medium difficulty)

Given a string of numbers, each number can represent several letters under the number key, and return all the possible composition of the letters under these numbers.

Solution 1 multiplication of definitions

I thought about using iteration and recursion, but I couldn't figure it out. I came up with this algorithm.

Consider the string "23" as ["a","b",c] * ["d","e","f"], and the multiplication can be realized by two for loops. You can see the code.

public List<String> letterCombinations(String digits) {
    List<String> ans = new ArrayList<String>();
    for (int i = 0; i < digits.length(); i++) {
        ans = mul(ans, getList(digits.charAt(i) - '0'));
    }
    return ans;

}

public List<String> getList(int digit) {
        String digitLetter[] = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
        List<String> ans = new ArrayList<String>();
        for (int i = 0; i < digitLetter[digit].length(); i++) {
            ans.add(digitLetter[digit].charAt(i) + "");
        }
          return ans;
    }
//Defined as multiplication of two lists
public List<String> mul(List<String> l1, List<String> l2) {
    if (l1.size() != 0 && l2.size() == 0) {
        return l1;
    }
    if (l1.size() == 0 && l2.size() != 0) {
        return l2;
    }
    List<String> ans = new ArrayList<String>();
    for (int i = 0; i < l1.size(); i++)
        for (int j = 0; j < l2.size(); j++) {
            ans.add(l1.get(i) + l2.get(j));
        }
    return ans;
}

Solution two queue iteration

Reference resources Here , someone wrote it in iteration. Mainly used the queue.

public List<String> letterCombinations(String digits) {
        LinkedList<String> ans = new LinkedList<String>();
        if(digits.isEmpty()) return ans;
        String[] mapping = new String[] {"0", "1", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        ans.add("");
        for(int i =0; i<digits.length();i++){
            int x = Character.getNumericValue(digits.charAt(i));
            while(ans.peek().length()==i){ //View team leader elements
                String t = ans.remove(); //Team leader out
                for(char s : mapping[x].toCharArray())
                    ans.add(t+s);
            }
        }
        return ans;
    }

If it's 23, then

At the end of the first for cycle, it becomes a, b, c;

In the first time of the second for cycle, when cycle a is out of the team, d e f is added respectively and then in the team, it becomes b c ad ae af

In the second for cycle, the second while cycle b is out of the team, adding d e f to it, and then entering the team, it becomes c ad ae af bd be bf

The third while cycle c of the second for cycle is out of the team, adding d e f to it and then entering the team, it becomes ad AE AF BD be BF c D CE CF

In this way, when the queue element length is no longer equal to 1, a while loop will appear.

Solution three recursion

Reference resources Here

private static final String[] KEYS = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };

public List<String> letterCombinations(String digits) {
    if(digits.equals("")) {
        return new ArrayList<String>();
    }
    List<String> ret = new LinkedList<String>();
    combination("", digits, 0, ret);
    return ret;
}

private void combination(String prefix, String digits, int offset, List<String> ret) {
    //offset represents which number to add
    if (offset == digits.length()) {
        ret.add(prefix);
        return;
    }
    String letters = KEYS[(digits.charAt(offset) - '0')];
    for (int i = 0; i < letters.length(); i++) {
        combination(prefix + letters.charAt(i), digits, offset + 1, ret);
    }
}

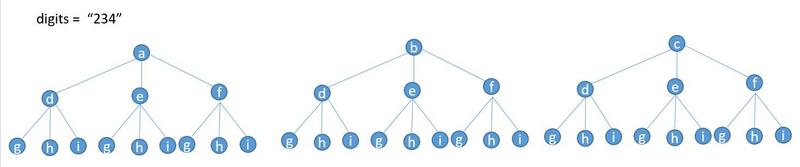
Starting from a, then recursion to d, then g, then add adg, then add adh, then add adi... From left to right, recursion to the end, then add it.

total

The time complexity and space complexity of this kind of questions are not clear, so they are not written.

For more details, please refer to leetcode.wang .