1706. Where does the ball meet Problem solution
Title Source: 1706. Where does the ball meet
2022.02.24 one question per day
Daily question column address: LeetCode daily problem solution is being updated ❤️💕
Today's topic is easier. After solving the problem, I'll pack my bags and go back to school tomorrow. I hope it's easy tomorrow, hehe
Today's topic is easy to understand, which is to simulate the walking path of a small ball
We can split the walking path of the small ball. From A to B in the figure, we will find that the walking of the small ball is divided into three parts
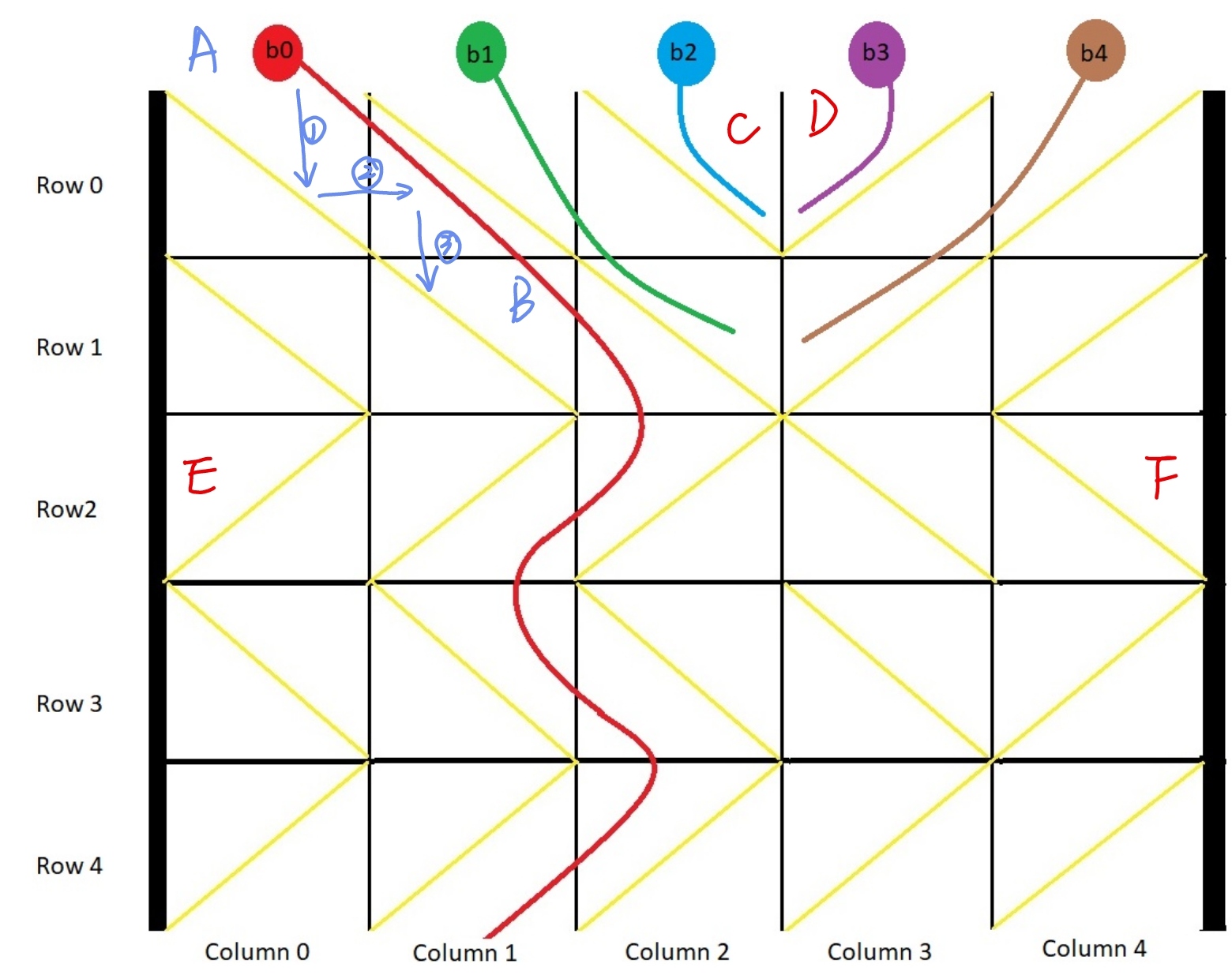
Therefore, in the first layer, we only need to count the changes of col
Method 1: simulation method
The first is the simulation method, that is, simple simulation. You can change the col value of the ball
class Solution {
public:
int m, n;
vector<int> findBall(vector<vector<int>> &grid) {
// Counts the length and width of a given array
m = grid.size(), n = grid[0].size();
// Give the result array in advance
vector<int> res(n, -1);
// Simulate the action route of traversing each small ball
for (int i = 0; i < n; i++) {
// First, define a variable to mark the position of the ball
int col = i;
// Traverse the corresponding position of each row
for (vector<int> row: grid) {
int temp = row[col];
// Update the position of the ball
col += row[col];
// If the position of the ball is updated and outside the array, it proves that the ball is stuck in the frame
// If the two positions of the small ball are not equal, it means that the small ball is stuck in a V
if (col < 0 || col >= n || temp != row[col]) {
// It proves that the ball has been stuck and can't continue to dive
col = -1;
break;
}
}
// If the last coordinate of the ball is not - 1, it proves that the ball has escaped successfully, and the value in the result array is updated
if (col >= 0) {
res[i] = col;
}
}
return res;
}
};
class Solution {
int m, n;
public int[] findBall(int[][] grid) {
// Counts the length and width of a given array
m = grid.length;
n = grid[0].length;
// Give the result array in advance
int[] res = new int[n];
Arrays.fill(res, -1);
// Simulate the action route of traversing each small ball
for (int i = 0; i < n; i++) {
// First, define a variable to mark the position of the ball
int col = i;
// Traverse the corresponding position of each row
for (int[] row : grid) {
int temp = row[col];
// Update the position of the ball
col += row[col];
// If the position of the ball is updated and outside the array, it proves that the ball is stuck in the frame
// If the two positions of the small ball are not equal, it means that the small ball is stuck in a V
if (col < 0 || col >= n || temp != row[col]) {
// It proves that the ball has been stuck and can't continue to dive
col = -1;
break;
}
}
// If the last coordinate of the ball is not - 1, it proves that the ball has escaped successfully, and the value in the result array is updated
if (col >= 0) {
res[i] = col;
}
}
return res;
}
}
Method 2: DFS
The next step is DFS,
First, we need to find out when the ball gets stuck
There are four situations in total, including C, D, E and F in the picture
After removing these four cases, the ball changes its col position, and the value of row will increase by 1
The end condition is that either the ball is stuck or the value of row is greater than the value of m
Then it's simple. Let's write the code
class Solution {
public:
int m, n;
vector<vector<int>> grid;
vector<int> findBall(vector<vector<int>> &grid) {
// Counts the length and width of a given array
m = grid.size(), n = grid[0].size();
this->grid = grid;
// Define result array
vector<int> res;
// Traverse the ball and perform recursive operation
for (int i = 0; i < n; i++) {
res.push_back(dfs(0, i));
}
return res;
}
int dfs(int i, int j) {
// Simulate the jamming of E and F
if ((j == n - 1 && grid[i][j] == 1) || (j == 0 && grid[i][j] == -1))
return -1;
// Simulate the situation that the ball is stuck by V-shape
if (grid[i][j]!=grid[i][j+grid[i][j]])
return -1;
// If it is at the bottom, just update the position of the ball (i.e. step 3)
if (i == m - 1)
return j + grid[i][j];
// If the meaning condition is not satisfied, it indicates that the ball is still falling, and recursion continues
return dfs(i + 1, j + grid[i][j]);
}
};
class Solution {
int m, n;
int[][] grid;
int[] findBall(int[][] grid) {
// Counts the length and width of a given array
m = grid.length;
n = grid[0].length;
this.grid = grid;
// Define result array
int[] res = new int[n];
// Traverse the ball and perform recursive operation
for (int i = 0; i < n; i++) {
res[i] = dfs(0, i);
}
return res;
}
int dfs(int i, int j) {
// Simulate the jamming of E and F
if ((j == n - 1 && grid[i][j] == 1) || (j == 0 && grid[i][j] == -1)) return -1;
// Simulate the situation that the ball is stuck by V-shape
if (grid[i][j] != grid[i][j + grid[i][j]]) return -1;
// If it is at the bottom, just update the position of the ball (i.e. step 3)
if (i == m - 1) return j + grid[i][j];
// If the meaning condition is not satisfied, it indicates that the ball is still falling, and recursion continues
return dfs(i + 1, j + grid[i][j]);
}
}
Method 3: dynamic programming
Finally, the method of dynamic programming
When recursing just now, we can find such a rule g r i d [ i ] [ j ] = = g r i d [ i ] [ j + g r i d [ i ] [ j ] ] grid[i][j]==grid[i][j+grid[i][j]] grid[i][j]==grid[i][j+grid[i][j]]
Our problem is to determine which channel the ball can finally fall out of
Let's change our mind
Which balls can fall out of each exit
Let's convert the formula g r i d [ i ] [ j − g r i d [ i ] [ j ] ] = = g r i d [ i ] [ j ] grid[i][j-grid[i][j]]==grid[i][j] grid[i][j−grid[i][j]]==grid[i][j]
Look up the entrance from the exit. The small ball that cannot find the entrance is the small ball (- 1) that will be stuck on the way
Direct code
class Solution {
public:
vector<int> findBall(vector<vector<int>> &grid) {
int m, n;
// Counts the length and width of a given array
m = grid.size(), n = grid[0].size();
// Create a marker array. res[0] is the initial state of the ball. The default value is - 1. It cannot reach the exit by default
vector<vector<int>> res(m + 1, vector<int>(n, -1));
// Give the initial value of dynamic programming
// The value in the exit grid is the col where the exit is located
for (int i = 0; i < n; i++) res[m][i] = i;
// Perform dp
for (int row = m - 1; row >= 0; row--)
for (int col = 0; col < n; col++) {
// If it is not in this range n, the ball has been stuck
if (col - grid[row][col] < 0 || col - grid[row][col] >= n) continue;
if (grid[row][col] == grid[row][col - grid[row][col]])
res[row][col - grid[row][col]] = res[row + 1][col];
}
return res[0];
}
};
class Solution {
public int[] findBall(int[][] grid) {
int m, n;
// Counts the length and width of a given array
m = grid.length;
n = grid[0].length;
// Create a marker array. res[0] is the initial state of the ball. The default value is - 1. It cannot reach the exit by default
int[][] res = new int[m + 1][n];
for (int i = 0; i < m + 1; i++)
for (int j = 0; j < n; j++)
res[i][j] = -1;
// Give the initial value of dynamic programming
// The value in the exit grid is the col where the exit is located
for (int i = 0; i < n; i++) res[m][i] = i;
// Perform dp
for (int row = m - 1; row >= 0; row--)
for (int col = 0; col < n; col++) {
// If it is not in this range n, the ball has been stuck
if (col - grid[row][col] < 0 || col - grid[row][col] >= n) continue;
if (grid[row][col] == grid[row][col - grid[row][col]])
res[row][col - grid[row][col]] = res[row + 1][col];
}
return res[0];
}
}
Note: I don't know if there is a better way to fill the two-dimensional array with Java (please forgive me for learning Java by yourself at the beginning), and please give me some advice