Reverses the binary bit of a given 32-bit unsigned integer.

Tips:

• Note that in some languages, such as Java, there are no unsigned integer types. In this case, both input and output are specified as signed integer types and should not affect your implementation, since the internal binary representation of integers is the same whether they are signed or unsigned.
• In Java, the compiler uses Binary complement Notation is used to represent signed integers. Therefore, in example 2 above, the input represents a signed integer -3 and the output represents a signed integer -1073741825.

Advanced:
How will you optimize your algorithm if you call this function multiple times?

Example 1:

Input: n = 00000010100101000001111010011100
 Output: 964176192 (00111001011110000010100101000000)
Interpretation: The input binary string 00000010100101000001111010011100 represents an unsigned integer 43261596.
     So it returns 964176192 with a binary representation of 00111001011110000010100101000000.

Example 2:

Input: n = 11111111111111111111111111111101
 Output: 3221225471 (10111111111111111111111111111111)
Interpretation: The input binary string 11111111111111111111111111101 represents an unsigned integer 4294967293.
     Therefore, 3221225471 is returned with a binary representation of 10111111111111111111111111111.

Tips:

• The input is a binary string of length 32

Method 1: Invert one by one

• Consider n as a 32-bit binary string, enumerate each of N from low to high, and add it in reverse order to the flip result.
• After each bit is enumerated, move n one bit to the right so that the lowest bit of the current n is the bit to be enumerated.
• End the loop when n = 0.

There are no unsigned integer types in some languages, such as Java. Logical right shift >> should be used for right shift of n.

Complexity analysis

• Time complexity: O(logn).

• Spatial complexity: O(1).

public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        int reverse = 0;

        // Bitwise flip of 32-bit unsigned integer
        for(int i = 0; i < 32; i ++){
            // reverse
            reverse = reverse << 1;
            // Put the last of n in
            // First use n&1 to take out the last digit
            // Put the last bit in reverse
            // | or operation: As long as there is one 1, it is 1 and both are 0 that is 0
            reverse = reverse | (n & 1);
            // +Operation: 0+1 = 1; 0+0 = 0; You can also put numbers in
            // reverse = reverse + (n & 1);

            // Move n one bit to the right, remove the last digit, and go to the next flip
            n = n >> 1;
        }

        return reverse;
    }
}

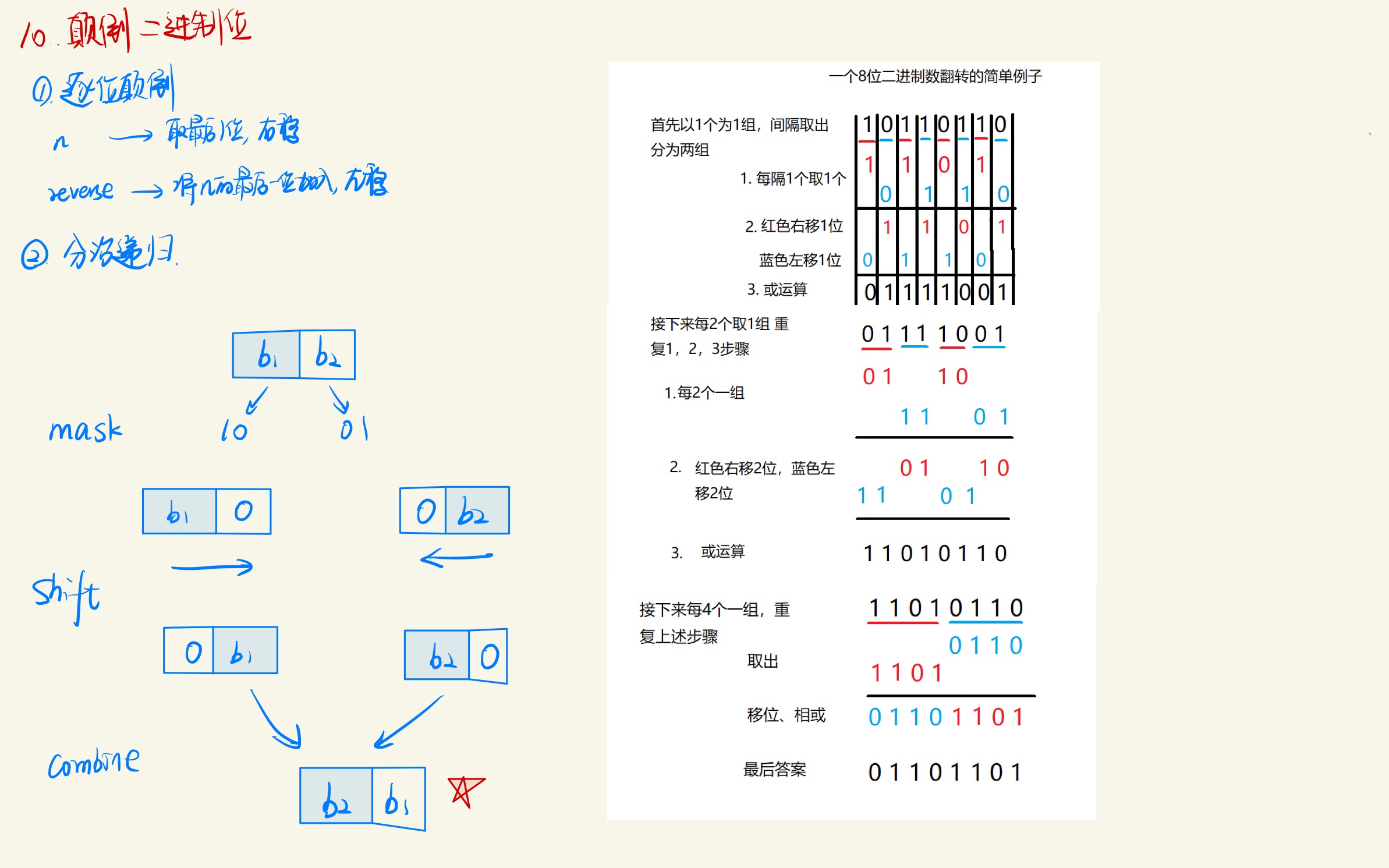
Method 2: Bit operation division: Two-digit interchange->Four-digit interchange->Eight-digit interchange->Sixteen-digit interchange

• To flip a binary string, divide it into left and right parts, perform the flip operation on each part recursively, and then put the left part behind the right part, which completes the flip. Because the left and right parts are computed similarly, this process can be accomplished from bottom to top using bit masking and displacement operations.
• For the bottom level of recursion, all parity bits need to be swapped:
  • Take out all odd and even digits;
  • Moves an odd number of displacements to an even number of digits.

• Similarly, for the second-to-last layer, each two-digit group takes out all odd and even arrays by the array number, and moves the odd arrays onto even arrays, and even arrays onto odd arrays. Follow up with the above.

Bit mask: https://www.sohu.com/a/452269753_505818      

There are no unsigned integer types in some languages, such as Java, and logical right shift >> should be used for n.

Complexity analysis

• Time complexity: O(1).

• Spatial complexity: O(1).

public class Solution {
    // you need treat n as an unsigned value
    // Hexadecimal representation bitmask example
    private static final int num1 = 0x55555555; // 01010101010101010101010101010101
    private static final int num2 = 0x33333333; // 00110011001100110011001100110011
    private static final int num3 = 0x0f0f0f0f; // 00001111000011110000111100001111
    private static final int num4 = 0x00ff00ff; // 00000000111111110000000011111111

    public int reverseBits(int n) {

        // Divide and conquer recursion
        n = ((n & 0xaaaaaaaa) >>> 1) | ((n & 0x55555555) << 1);
        n = ((n & 0xcccccccc) >>> 2) | ((n & 0x33333333) << 2);
        n = ((n & 0xf0f0f0f0) >>> 4) | ((n & 0x0f0f0f0f) << 4);
        n = ((n & 0xff00ff00) >>> 8) | ((n & 0x00ff00ff) << 8);
        n = (n >>> 16) | (n << 16);

        return n;
    }
}