A center

The center of   heap is dynamic extremum, which is indispensable.

1046. Weight of the last stone

There is a pile of stones, and the weight of each stone is a positive integer.
Each round, choose the two heaviest stones and crush them together. Suppose the weight of the stone is x and Y respectively, and x < = y. Then the possible results of crushing are as follows:
If x == y, both stones will be completely crushed;
If x= y. Then the stone weighing x will be completely crushed, and the new weight of the stone weighing y will be y-x.
In the end, there will be only one stone left at most. Returns the weight of this stone. If there are no stones left, return 0.

Example:

Input: [2,7,4,1,8,1]
Output: 1
Explanation:
First select 7 and 8 to get 1, so the array is converted to [2,4,1,1,1],
Then select 2 and 4 to get 2, so the array is converted to [2,1,1,1],
Then 2 and 1, get 1, so the array is converted to [1,1,1],
Finally, select 1 and 1, get 0, and finally convert the array to [1], which is the weight of the last remaining stone.

Idea:

When using the small top reactor to simulate the large top reactor, the opposite number needs to be taken into the reactor and out of the reactor

class Solution:
    def lastStoneWeight(self, stones: List[int]) -> int:
        # Using python small top heap to construct large top heap
        heap = [-stone for stone in stones]
        # Build binary heap
        heapq.heapify(heap)

        while len(heap) > 1:
            # Pop up two header elements in turn
            x,y = heapq.heappop(heap),heapq.heappop(heap)
            if x != y:
                #Add to both list and heap
                heapq.heappush(heap,x-y)
        if heap:
            return -heap[0]
        return 0

Three skills

Skill 1: fixed heap
  this technique refers to the size of the fixed heap k k k remains unchanged, and the code can be implemented by pushing in one pop out of each pop. Since the initial heap may be 0, we need to push into the heap one by one at the beginning to reach the size of the heap k k k. Therefore, strictly speaking, the size of the heap should not be greater than k k k.
This technique can be used to find the smallest value of k or the largest value of k.

For example, find the small value of k
Idea: build a large top heap and keep the size of the heap at K. if the size of the heap is greater than k after joining the team, remove the larger number compared with the newly joined elements and the top of the heap, so as to ensure that the elements in the heap are the smallest K of all elements. At this time, the elements at the top of the heap are the smaller value of K. The heap is the smallest number of K, and the top of the heap is the largest, so the top of the heap is the smallest K

In summary:

1. For a large top heap with a fixed size of k, you can quickly find the smallest value of k
2. For a small top heap with a fixed size of K, the k-th value can be quickly obtained

295. Median data flow

  this problem is based on the fixed heap technique. Using the properties of large top heap and small top heap, we can quickly find the median. For example, the number of data is n n n. The number of large top heap elements is n + 1 2 \frac{n+1}2 2n+1, number of small top heap elements n − n + 1 2 n-\frac{n+1}2 N − 2n+1, then 0 < = n + 1 2 − ( n − n + 1 2 ) < = 1 0<=\frac{n+1}2-(n-\frac{n+1}2)<=1 0 < = 2n+1 − (n − 2n+1) < = 1, when n is an odd number, = 1 =1 =1.

The median is the number in the middle of the sequence table. If the list length is even, the median is the average of the middle two numbers.
For example,
The median of [2,3,4] is 3
The median of [2,3] is (2 + 3) / 2 = 2.5
Design a data structure that supports the following two operations:

• void addNum(int num) - adds an integer from the data stream to the data structure.
• double findMedian() - returns the median of all current elements.

Advanced:

• If all integers in the data stream are in the range of 0 to 100, how will you optimize your algorithm?
• If 99% of the integers in the data stream are in the range of 0 to 100, how will you optimize your algorithm?

Example:

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2

Idea 1: two heaps

An ordered array is divided into pre ordered array and post ordered array

Then the maximum heap is constructed by using the pre ordered array, and the minimum heap is constructed by using the post ordered array

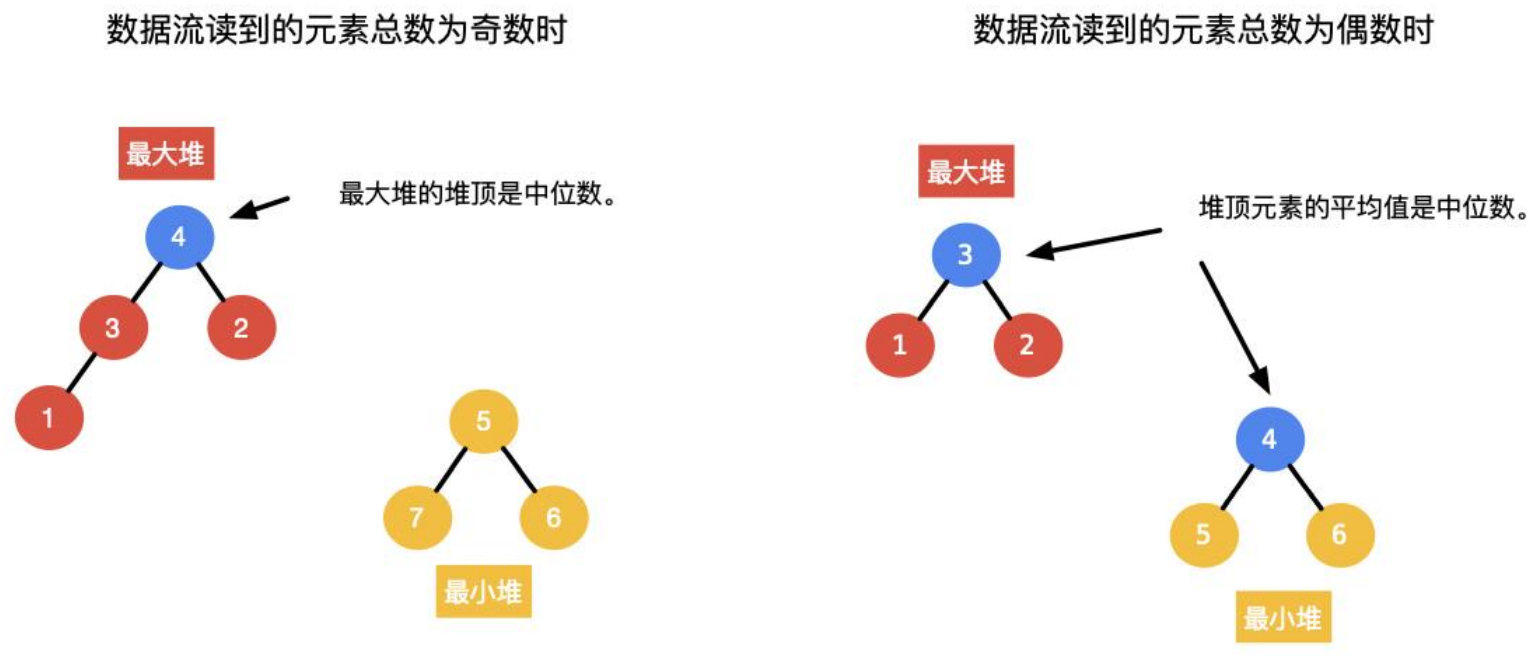
At this time, the maximum heap and the minimum heap have two properties:

• The maximum heap top element is less than the minimum heap top element
• The maximum number of heap elements is either equal to the minimum number of heap elements or one more element

Specific operation:

• Case 1: when the sum of the number of elements of two heaps is even, in order to make one more element in the maximum heap, this process is adopted: "maximum heap → minimum heap → maximum heap";
• Case 2: when the sum of the number of elements of the two heaps is odd, the minimum heap must have one more element, so that the number of elements of the maximum heap and the minimum heap are equal. Adopt the following process: "maximum heap → minimum heap].

class MedianFinder:

    def __init__(self):
        """
        initialize your data structure here.
        """
        # Sum of initialization elements, maximum heap, minimum heap
        self.count = 0
        self.max_heap = []
        self.min_heap = []

    # Add elements to the maximum heap and the minimum heap. The number of elements is different when the number of elements is odd and even
    def addNum(self, num: int) -> None:
        self.count += 1
        # python defines a small top heap, so you need to pass in the opposite number to simulate a large top heap
        heapq.heappush(self.max_heap,(-num,num))
        # Pop up the big top element
        _,max_heap_top = heapq.heappop(self.max_heap)
        # Construction of small top pile
        heapq.heappush(self.min_heap,max_heap_top)
        # If the number of elements is odd, the number of elements in the large top heap is 1 more than that in the small top heap
        if self.count & 1:
        	# Pop up small top element
            min_heap_top = heapq.heappop(self.min_heap)
            # Press the small top element into the large top
            heapq.heappush(self.max_heap,(-min_heap_top,min_heap_top))

    def findMedian(self) -> float:
        # If the number of elements is odd, the median is the top element of the large heap
        if self.count & 1:
            return self.max_heap[0][1]
        # If the number of elements is even, the median is the average of the top elements of the large top heap and the small top heap
        else:
            return (self.max_heap[0][1] + self.min_heap[0]) / 2

Skill 2: multi-channel merging
Multiple routes are reflected in: there are multiple candidate routes. In code, we can use multiple pointers to represent. Merging is reflected in: the result may be the longest or shortest among multiple candidate routes, or the k-th route, etc. Therefore, we need to compare the results of multiple routes and discard or select one or more routes according to the topic description.

1439. The k-th smallest array sum in the ordered matrix

Give you a matrix mat of m * n and an integer k. each row in the matrix is arranged in a non decreasing order.
You can select one element from each line to form an array. Returns the sum of the k th smallest array of all possible arrays.

Example:

Input: mat = [[1,3,11],[2,4,6]], k = 5
Output: 7
Explanation: select an element from each row. The first k and smallest arrays are:
[1,2], [1,4], [3,2], [3,4], [1,6]. The sum of the fifth is 7.

class Solution:
    def kthSmallest(self, mat: List[List[int]], k: int) -> int:
        # Initialize heap
        h = []
        # Yuanzu cur consists of two pieces of information. One is the sum of the first items of M one-dimensional arrays, which represents the sum of arrays, and the other is Yuanzu with length m and all filled with 0, which represents the array pointer
        cur = (sum(vec[0] for vec in mat),tuple([0]*len(mat)))
        # Put Yuanzu cur into the heap
        heapq.heappush(h,cur)
        # Avoid the same pointer being evaluated multiple times
        seen = set(cur)

        for _ in range(k):
            # acc indicates the current and pointer conditions
            acc,pointers = heapq.heappop(h)
            # Brutally move a pointer in the pointer array every time. Every time you move a pointer, it forks. The total possible movement is n, where n is the length of one-dimensional array.
            for i,pointer in enumerate(pointers):
                # If pointer == len(mat[0]) - 1, it means the end is reached and cannot be moved
                if pointer != len(mat[0]) - 1:
                    # If there is no end, the pointer moves one bit. At this time, it is necessary to judge whether the pointer we want to move appears in the hash table
                    t = list(pointers)
                    t[i] = pointer + 1
                    tt = tuple(t)
                    # If it already appears in the hash table, skip it. Otherwise, add it to the hash table
                    if tt not in seen:
                        seen.add(tt)
                        # Add heap
                        heapq.heappush(h,(acc + mat[i][pointer + 1]- mat[i][pointer], tt))
        return acc

264. Ugly number II

Give you an integer n, please find out and return the nth ugly number.
Ugly numbers are positive integers that contain only prime factors 2, 3, and / or 5.

Example:

Input: n = 10
Output: 12
Explanation: [1, 2, 3, 4, 5, 6, 8, 9, 10, 12] is a sequence composed of the first 10 ugly numbers.

Idea 1: priority queue (small root heap)

A simple solution is to use priority queues

1. First put the minimum ugly number 1 into the queue shape
2. Take out the minimum value x from the queue each time, and then queue the ugly numbers 2x, 3x and 5x corresponding to X.
3. Repeat step 2 for many times, and the value of the nth time out of the queue is the answer.

In order to prevent the same ugly number from entering the queue multiple times, we need to use the data structure Set to record the ugly numbers that have entered the queue.

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        nums = [2,3,5]
        # The hash table is used to record the ugly number in the heap to prevent the same ugly number from entering the heap multiple times
        explored = {1}
        # Minimum number of heap records
        pq = [1]
        for i in range(1,n+1):
            # Take the minimum value from the heap
            x = heapq.heappop(pq)
            # i==n means the nth time out of the team
            if i == n:
                return x
            for num in nums:
                t = num * x
                # If the newly generated ugly number has not been added to the heap, it is added to the hash table and the minimum heap
                if t not in explored:
                    explored.add(t)
                    heapq.heappush(pq,t)

Idea 2: multi-channel merging

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        # ans is used to store existing data
        ans = [0] * (n+1)
        # Store from subscript 1, and the first ugly number is 1
        ans[1] = 1
        #Because the three ordered sequences are derived from the existing ugly number * prime factor
        # i2, i3 and i5 respectively represent the existing ugly number subscript (starting with 1) of the three ordered sequences
        i2 = i3= i5 = 1
        idx = 2
        while idx <= n:
            # From ans[ix]*X, we can get which bit the current ordered sequence points to
            a,b,c = ans[i2]*2,ans[i3]*3,ans[i5]*5
            # Store the smallest bit of the three ordered sequences into the existing ugly number sequence and move its subscript back
            m = min(a,b,c)
            if m == a:
                i2 += 1
            if m == b:
                i3 += 1
            if m == c:
                i5 += 1
            ans[idx] = m
            # ans subscript backward
            idx += 1
        # The cycle end condition is idx = n+1
        return ans[n]

Skill 3: Little Zhuge after the event
  this technique refers to: when traversing from left to right, we don't know what the right is. We don't know until you get to the right. If you want to know what is on the right, a simple way is to traverse twice. The first traverse records the data. When the second traverse, use the data recorded in the last traverse. This is the way we use most. However, sometimes we can also go back after traversing the specified element, so that we can store while traversing and use one traversal.
  specifically, it is to collect all the data from left to right, and select one from the inside when it needs to be used. If we all want to take the maximum or minimum value and the extreme value will change, we can use heap acceleration. Intuitively, it is to use the time machine to go back to the front and achieve the purpose of hindsight.

871. Minimum refueling times

The car starts from the starting point to the destination, which is located at target miles east of the starting position.
There are gas stations along the way, and each station[i] represents a gas station. It is located at station[i][0] miles east of the starting position, and there are station[i][1] liters of gasoline.
Suppose the capacity of the car's fuel tank is unlimited, with startFuel liters of fuel initially. It uses a liter of gasoline every mile it travels.
When the car arrives at the gas station, it may stop to refuel and transfer all the gasoline from the gas station to the car.
What is the minimum number of times a car needs to refuel in order to reach its destination? If the destination cannot be reached, - 1 is returned.
be careful:
If the remaining fuel is 0 when the car arrives at the gas station, it can still refuel there. If the remaining fuel is 0 when the car reaches its destination, it is still considered to have reached its destination.

Example:

Input: target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
Output: 2
Explanation:
We had 10 litres of fuel when we set out.
We drove to the gas station 10 miles from the starting point and consumed 10 litres of fuel. Increase the gasoline from 0 liters to 60 liters.
Then we drove from the gas station 10 miles to the gas station 60 miles (consuming 50 litres of fuel),
And increase the gasoline from 10 liters to 50 liters. Then we drove to our destination.
We stopped at two gas stations along the way, so we returned to 2.

Train of thought: be wise after the event

First traverse the station, and then construct a large top stack. Each time, judge whether the current gasoline is enough to reach the next gasoline station. If enough, continue; If not enough, choose to refuel at the station with the most gasoline in the passed location

class Solution:
    def minRefuelStops(self, target: int, startFuel: int, stations: List[List[int]]) -> int:
        stations += [(target,0)]
        # Fuel just started
        cur = startFuel
        ans = 0

        # Maximum heap
        h = []
        # Last position
        last = 0
        for i,fuel in stations:
            # How many litres of gasoline are there at present? i indicates the current location of the gas station
            cur -= i - last
            # If cur < 0 and h is not empty, refueling is required
            while cur < 0 and h:
                # Refuel at the station with the most gasoline in the passed position
                cur -= heapq.heappop(h)
                ans += 1
            
            # The cycle end condition is cur > = 0 or h is empty. When cur < 0, h is empty and cannot reach the end
            if cur < 0:
                return -1

            # Construction of large top pile
            heapq.heappush(h,-fuel)
            # Update location
            last = i
        return ans

1642. Farthest accessible building

Give you an integer array heights, which represents the height of the building. There are also some brick bricks and ladder ladders.
You start your journey from building 0 and continue to move towards the building behind you, during which you may use bricks or ladders.
When moving from building i to building i+1 (subscript starts from 0):

• If the height of the current building is greater than or equal to the height of the next building, ladders or bricks are not required
• If the height of the current building is less than the height of the next building, you can use a ladder or (h[i+1] - h[i]) bricks
• If you use a given ladder and brick in the best way, return the subscript of the farthest building you can reach (starting from 0).

Example:

Input: hedders = 12,4,4,7,7,7,6,6,6,7
Output: 4
Explanation: starting from building 0, you can complete the journey according to this scheme:

• Do not use bricks or ladders to reach Building 1 because 4 > = 2
• Use 5 bricks to reach Building 2. You must use bricks or ladders because 2 < 7
• Do not use bricks or ladders to reach building 3 because 7 > = 6
• Use a unique ladder to reach building 4. You must use bricks or ladders because 6 < 9 cannot cross building 4 because there are no more bricks or ladders.

Train of thought: be wise after the event

First traverse diff (the height difference of the building to be crossed), and then construct a large top pile. When the bricks are not enough, we should use a ladder. At this time, replace the top element of the largest pile in front with a ladder. Because the front is made of bricks, it is equivalent to replacing the ladder with bricks

class Solution:
    def furthestBuilding(self, heights: List[int], bricks: int, ladders: int) -> int:
        # Maximum heap
        h = []
        for i in range(1,len(heights)):
            diff = heights[i] - heights[i-1]
            # If the height difference is less than or equal to 0, ladders or bricks are not required
            if diff <= 0:
                continue
            # If the number of bricks is less than the height difference and there is a ladder, the ladder is used
            if bricks < diff and ladders > 0:
                ladders -= 1
                # The maximum height difference in front is greater than that in the present, which means that bricks are wasted in front and ladders should be used, which is equivalent to converting into bricks
                if h and -h[0] > diff:
                    # This situation can be converted into bricks
                    bricks -= heapq.heappop(h)
                else:
                    continue
            # If the number of bricks is greater than the height difference, use bricks
            bricks -= diff
            # If the current number of bricks is less than 0, it indicates that the current building cannot be reached, and the subscript of the previous building is returned
            if bricks < 0:
                return i - 1
            heapq.heappush(h,-diff)
        
        return len(heights) - 1

If it's helpful to you, please praise and pay attention, which is really important to me!!! If you need to communicate with each other, please comment or send a private letter!