Topic Description

Given an integer array nums,
Find the sum of elements in the range of index I to J (i < j) of an array
 Including I and J.

    The update(i, val) function can modify the column by updating the value subscribed to I to val.
    
    Examples:
    
    Given nums = [1, 3, 5]
    
    sumRange(0, 2) -> 9
    update(1, 2)
    sumRange(0, 2) -> 8
    Explain:
    
    Arrays can only be modified under the update function.
    You can assume that the number of calls to the update function and the sumRange function is uniformly distributed.
    
    Source: LeetCode
    Link: https://leetcode-cn.com/problems/range-sum-query-mutable

[LeetCode]-303. Region and retrieval-array immutable
This is a simple version of this question, you can go to see this question first, which uses caching method.

There are two ways to solve this problem. (I understand the two ways.) Of course, there are more ways. You can comment below.

Method 1: Direct modification

Time complexity: O(1) update query O(n) summation
For regions and retrieval, we access each element from an array at a fixed time, and in the worst case, we access n elements. Therefore, the time complexity is O(n). Time complexity of updating queries O(1)

   public int sumRange(int i, int j) {
            int sum = 0;
            for (int l = i; l <= j; l++) {
                sum += data[l];
            }
            return sum;
        }
    
    public int update(int i, int val) {
        nums[i] = val;
    }

Method 2: Segment Tree
Time complexity: O(logn). The time complexity of the algorithm is O(logn), because there are several tree nodes whose ranges include elements of the ii array, one at each level. There are log (n) levels.
Spatial complexity: O(1)

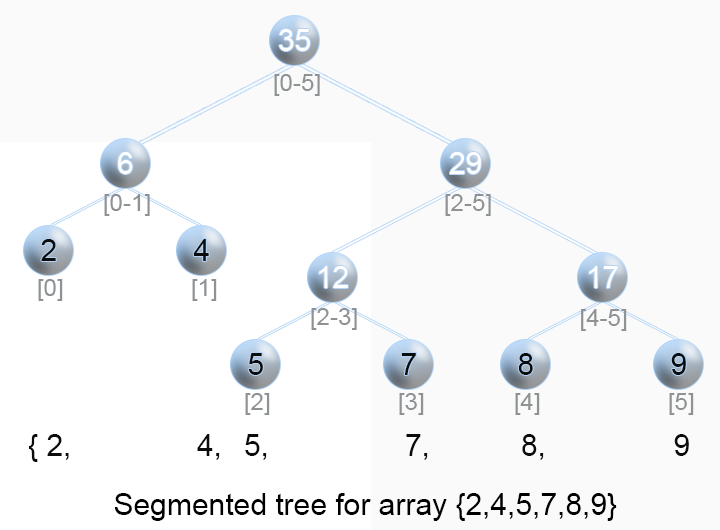
Step 1: Construct a segment tree

Line segment tree is similar to complete binary tree, but some nodes have only one left or right child. In order to construct a complete binary tree for calculation, you can add some virtual nodes by yourself, and the virtual node value is set to 0.
This example is constructed with arrays

//An arr ay tree representing the stored value is a segment tree node representing the current node.
void build_tree(int arr[],int tree[],int node,int start,int end)
{
	if(start!=end)
	{
int mid = (start+end)/2;  //Divide the array into two halves and fill in the virtual node 0 at each uneven recursive node.
	int left_node = 2*node+1;  //Index of left node
	int right_node = 2*node+2; //Right node
	
	//A recursive build stops recursion until start= end has only one value, tree[node] = arr[start] or arr[end]
	build_tree(arr,tree,left_node,start,mid);   
	build_tree(arr,tree,right_node,mid+1,end);
	
	tree[node] = tree[left_node]+tree[right_node];  //Backtracking the value of each parent node is the sum of two child nodes
	//Some parent nodes have only one child node, so building virtual node 0 has no effect.
	}
	else
	{
		tree[node] = arr[start];
	}
	
	
}

Step 2: Summation

If you sum, you can decide whether the sum range is on the left subtree or on the right.
L R represents the beginning and end of sum range
There are two situations in the picture above.
1. Find the sum of [4-5] and then recurse directly to the right.
2. To find [1-5], we must first calculate [4-5] on the right side of recursion and then calculate the final sum of [1].
The code is as follows

int sumRange(int arr[],int tree[],int node,int start,int end,int L,int R)
{
	if(R<start || L>end)  //If the sum range is calculated directly on the left or right side, the other side can return 0. 
	{
		return 0; //If the sum range is calculated directly on the left or right side, the other side can return 0. 
	}
	else if(L<=start&&R>=end) //The result of the predicted block can be returned directly in the middle of L R without recursive summation. 
	{
		return tree[node]; 
	}
	else //If the sum range cannot be returned directly, the left and right subtrees are recursively in the start end range.
	{
		int mid = (start+end)/2;
		int left_node = 2*node+1;
		int right_node = 2*node+2;
		int sum_left = sumRange(arr,tree,left_node,start,mid,L,R);
		int sum_right = sumRange(arr,tree,right_node,mid+1,end,L,R);
		return sum_left+sum_right;
	}
}

Step 3: Update
Updating Compare Number Understanding is the process of finding nodes

index Represents the updated location val Representative value
void update_tree(int arr[],int tree[],int node,int start,int end,int index,int val)
{
	
	if(start==end)
	{
		arr[index] = val;
		tree[node] = val;
	}
	else
	{
		int mid = (start+end)/2;
		int left_node = 2*node+1;
		int right_node = 2*node+2;
		
		if(index >=start && index<=mid)
		{
			update_tree(arr,tree,left_node,start,mid,index,val);
		}
		else
		{
			update_tree(arr,tree,right_node,mid+1,end,index,val);
		}
		
		tree[node] = tree[left_node]+tree[right_node];
	}
}

Principal function

	int arr[] = {1,3,5,7,9,11};
	int size=6;
	int tree[1000] = {0};
	
	build_tree(arr,tree,0,0,size-1);
	update_tree(arr,tree,0,0,size-1,4,6);
	int s =sumRange(arr,tree,0,0,size-1,2,5);
	cout<<s;

summary

The segment tree is actually dichotomy plus recursion.
If update time complexity is changed to O (1) without segment tree, then summation will be changed to O (n) again.