Give you a non negative integer ， num ， represented by a string and an integer ， k ， and remove the ， k ， digits in this number to minimize the remaining numbers. Please return this minimum number as a string.

Example 1:

Input: num = "1432219", k = 3
 Output: "1219"
Explanation: remove the three numbers 4, 3, and 2 to form a new minimum number 1219.

Example 2:

Input: num = "10200", k = 1
 Output: "200"
Explanation: remove the first 1 and the remaining number is 200 Note that the output cannot have any leading zeros.

Example 3:

Input: num = "10", k = 2
 Output: '0'
Explanation: remove all numbers from the original number. If the rest is empty, it is 0.

Tips:

• 1 <= k <= num.length <= 10^5
• num ， consists of only a few digits (0 - 9)
• num ， does not contain any leading zeros except ， 0 ， itself

Give an integer, remove k numbers from the integer, and require the remaining numbers to form a new integer as small as possible. How should I select the removed number?

Where the length of the integer is greater than or equal to k, the size of the given integer can exceed the number range of long type.  

• Problem simplification: if only one number is deleted, that is, k = 1, how to minimize the new integer value?
  • Not only the size of the number itself, but also the influence of location should be considered—— The highest bit of an integer is reduced by 1, which has a great impact on the value.
  • Taking 541 270 936 as an example, the result after removing a number is from a 9-bit integer to an 8-bit integer—— Since it is also an 8-bit integer, it is obvious that the high-order number should be reduced first, which has the greatest impact on the new value.
• How to lower the high number?
  • Compare all numbers of the original integer from left to right. If a digit is found to be larger than the digit on its right, the value of the digit will be reduced after deleting the digit, because the smaller digit on the right replaces its position.
• The local optimal solution is obtained in turn, and finally the idea of global optimal order is obtained, that is, greedy algorithm.  

For two sequences of numbers of the same length, the left most different number determines the size of the two numbers.

• For example, for A = 1axxx, B = 1bxxx, if a > b, then a > B.
• Based on this, in order to minimize the remaining numbers, it is necessary to ensure that the number in front is as small as possible.

e.g. given a number sequence, such as 425, if only one number is required to be deleted, there are three choices from left to right: 4, 2 ， and 5. Compare each number with its left neighbor. Starting from 2, 2 is smaller than its left neighbor 4. Assuming that the number 4 is retained, all possible combinations begin with the number 4 (i.e. 42, 45). On the contrary, if you remove 4 and leave 2, you get a combination starting with 2 (i.e. 25), which is significantly smaller than any combination leaving 4. Therefore, the number 4 should be removed. If you don't remove the number 4, no matter what number you remove, you won't get the lowest decimal.

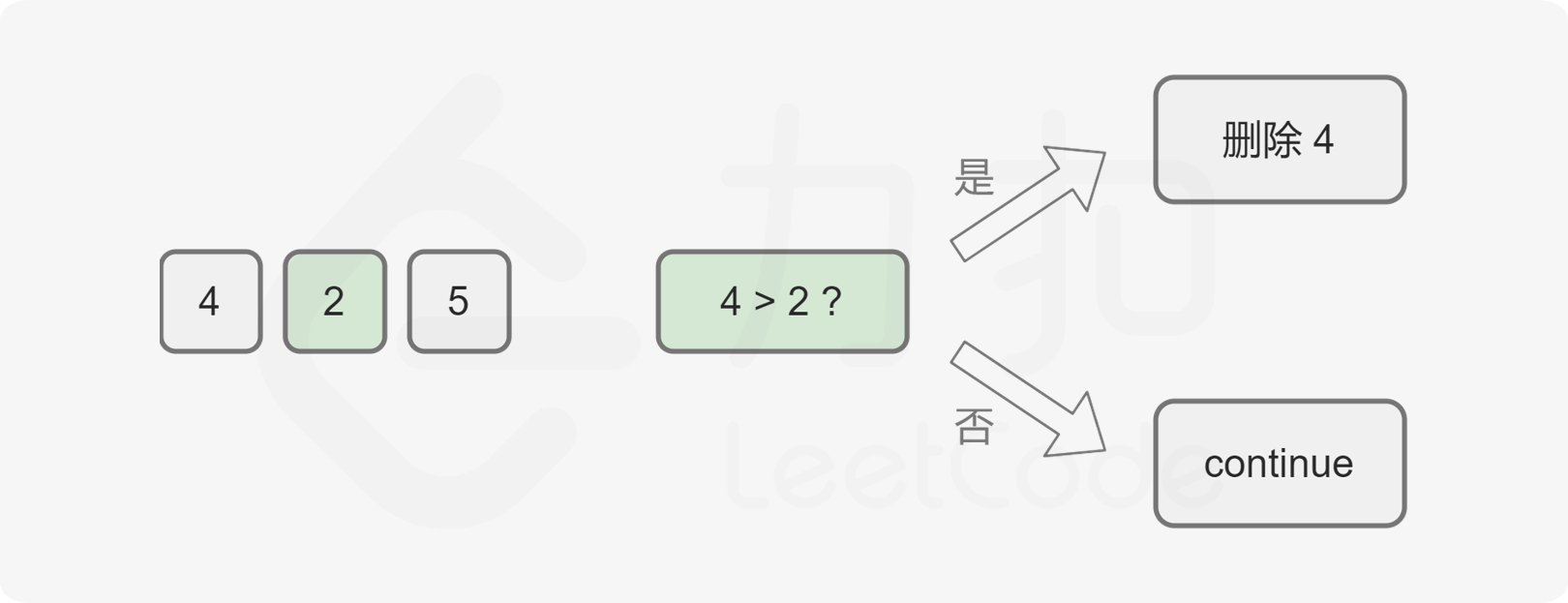
Based on the above analysis, the greedy strategy of "delete a number" can be obtained:

• Give a sequence of numbers of length n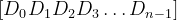, find the first position i (i > 0) from left to right so that 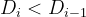, and delete 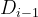； If it does not exist, it means that the whole number sequence is monotonous, and the last number can be deleted.
• Based on this, this strategy can be executed once for the whole digital sequence at a time; After deleting a character, the remaining number sequence of n − 1 length forms a new sub problem, and the same strategy can be used until k times.
• The worst implementation complexity of violence will reach O(nk) (considering that the whole number sequence is monotonous), and this process needs to be accelerated.

• Consider constructing the final answer in increments from left to right. A stack can be used to maintain the current answer sequence. The elements in the stack represent the minimum integer that can be obtained by deleting no more than k numbers as of the current position. According to the previous discussion: before using K deletion times, the sequence in the stack is monotonous from the bottom of the stack to the top of the stack.  

  • For each number, if the number is less than the top of the stack element, the top of the stack element is continuously popped until

    • Stack is empty

    • Or the new stack top element is not greater than the current number

    • Or k digits have been deleted

• After the above steps, additional processing needs to be done for some situations:
  • If M − numbers are deleted and m < k, in this case, additional k − m numbers need to be deleted from the end of the sequence.
  • If leading zeros exist in the final number sequence, the leading zeros shall be deleted.
  • If the final number sequence is empty, it should return 0.
• Finally, the answer sequence from the bottom of the stack to the top of the stack is the decimal.
  • Considering that the stack is characterized by last in first out, if it is implemented through the stack, you need to pop up the elements in the stack in turn and then flip them to get the minimum number. To avoid flipping operations, you can use double ended queues instead of stack implementations.

  • Time complexity: O(n), where n is the length of the string. Although there are nested loops, the inner loop runs up to k times. Since 0 < k ≤ n, the time complexity of the main cycle is limited to 2n. For logic outside the main loop, the time complexity is O(n), so the total time complexity is O(n).

  • Space complexity: O(n). Storing numbers on the stack requires linear space.

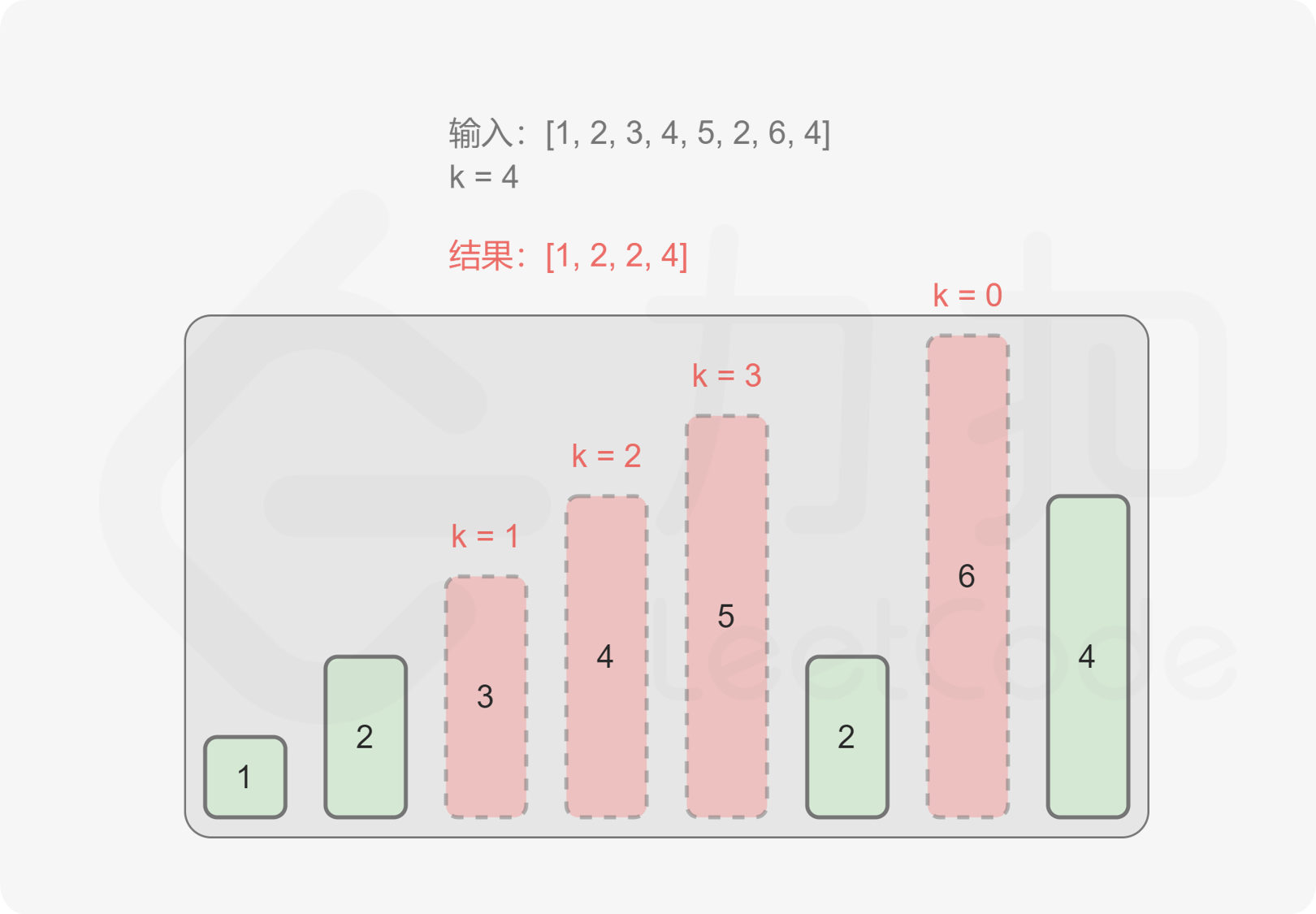
The most original idea is to reduce the highest value.  

• Use a double-layer loop. The number of outer loops is the number of numbers K to be deleted, and the inner loop compares all numbers from left to right. When the number to be deleted is traversed, the substring method of the string is used to delete the matched number, and the string is spliced again O(n*k)
• Performance issues
  • Each inner loop needs to traverse all numbers from scratch Stay at the last deleted position to continue the comparison;
  • The subString() method itself has poor performance—— The underlying implementation designs the creation of new strings and character by character replication. The time complexity of this method is O(n)—— You should avoid calling subString() every time you delete a number.

import java.util.*;

// Remove the K-bit numbers so that the new integer formed by the remaining numbers is as small as possible
public class DeleteKNumberMin {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc = new Scanner(System.in);
		while(sc.hasNext()) {
			String nums = sc.next();
			int k = sc.nextInt();
			
			System.out.println(removeKDigits(nums, k));
			
		}
		
		sc.close();
	}

	private static String removeKDigits(String nums, int k) {
		// TODO Auto-generated method stub
		// Delete k numbers and compare the sizes of adjacent elements
		// Traverse from left to right, find a number larger than the number on your right and delete it
		for(int i = 0; i < k; i ++) {
			boolean hasDelete = false;
			for(int j = 0; j < nums.length() - 1; j ++){
				if(nums.charAt(j) > nums.charAt(j+1)) {
					nums = nums.substring(0,j) + nums.substring(j+1,nums.length());
					hasDelete = true;
					break;
				}
			}
			
			// If the number to be deleted is not found, the last number is deleted
			if(hasDelete == false) {
				nums = nums.substring(0, nums.length()-1);
			}
		}
		
		// Clear the number 0 to the left of the integer
		int start = 0;
		for(int j = 0; j < nums.length() - 1; j ++) {
			if(nums.charAt(j) != '0') {
				break;
			}
			start ++;
		}
		nums = nums.substring(start,nums.length());
		
		// If all numbers of an integer are deleted, 0 is returned directly
		if(nums.length() == 0) {
			return "0";
		}
		
		return nums;
	}

}

Scheme optimization: greedy + monotone stack -- Take traversal number as outer loop and k as inner loop

import java.util.*;

// Use the monotone stack to store the final results for greedy search
public class DeleteKNumberMinSecond {

	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);
		while(sc.hasNext()) {
			String nums = sc.next();
			int k = sc.nextInt();
			
			System.out.println(removeKDigits(nums, k));
			
		}
		
		sc.close();
	}

	private static String removeKDigits(String nums, int k) {

		// Greedy + monotonic stack (using two terminal queue simulation to facilitate the output of results)
		Deque<Character> deque = new LinkedList<Character>();
		
		for(int i = 0; i < nums.length(); i ++) {
			char digit = nums.charAt(i);
			// Conditions for stack exit: the double ended stack is not empty, k > 0 (the number to be deleted has not been deleted), and the element at the top of the stack is greater than the current number
			// When the number at the top of the stack is greater than the current number traversed, the number at the top of the stack is out of the stack (equivalent to deleting the number)
			while(deque.isEmpty() == false && k > 0 && deque.peekLast() > digit) {
				deque.pollLast();
				k --;
			}
			// Stack the current number traversed
			deque.offerLast(digit);
		}
		
		/* Consider some additional situations
		 1,If M numbers are deleted and m < K, additional k-m numbers need to be deleted from the tail of the sequence.
		 2,If there are leading zeros in the final number sequence, delete the leading zeros.
		 3,Returns 0 if the final number sequence is empty. 
		 */
		for(int i = 0; i < k; i ++) {
			deque.pollLast();
		}
		
		StringBuilder result = new StringBuilder();
		boolean isBeginningZero = true;
		while(!deque.isEmpty()) {
			char digit = deque.pollFirst();
			if(isBeginningZero && digit != '0') {
				isBeginningZero = false;
			}
			
			if(isBeginningZero == false) {
				result.append(digit);
			}
		}
		
		if(result.length() == 0) {
			return "0";
		}
		
		return result.toString();
	}

}