1. Title

Given a matrix with M x N elements (M rows, N columns), return all the elements in the matrix in the order of diagonal traversal, as shown in the following figure.

Example:

input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]

output:  [1,2,4,7,5,3,6,8,9]

Explain:

1. The total number of elements in a given matrix does not exceed 10000.

2. Ideas

(simulation) O ( n ∗ m ) O(n*m) O(n∗m)

The most direct idea we can think of is to simulate a walking path in an array as required by the title, and then return all the elements in the matrix in the order in which they are diagonally traversed.

First, let's look at several properties of diagonals:

Looking at the entire matrix, we can see that each element in the first row corresponds to a diagonal line, and each element in the last column corresponds to a diagonal line, which contains the upper right diagonal line repeatedly. Therefore, if the number of rows and columns of the matrix is n and m, then the total number of diagonals is: n + m - 1. We numbered each diagonal as shown in the following figure:

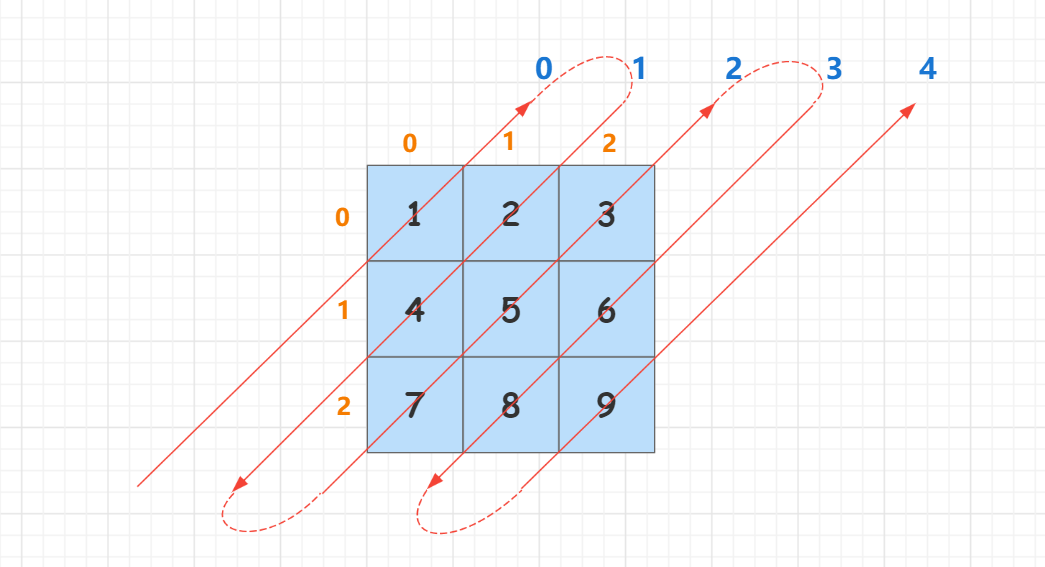
The top left corner is the 0th diagonal, and the bottom right corner is the n + m - 2 diagonal. Look at the direction of the diagonal line and notice that the direction of the diagonal line alternates upward or downward. When the sequence number of the diagonal line is even, the direction of the diagonal line is upward; When the sequence number of the diagonal is odd, the direction of the diagonal is downward.

Properties of matrix rows and columns:

The sum of the horizontal and vertical coordinates of each point (x, y) on the same diagonal line is equal to x + y and equals the sequence number of the diagonal line (look closely at the figure above).

How do I determine the start and end points of each diagonal?

Depending on the diagonal nature, if one of the vertical and horizontal coordinates of the endpoint is known, another dimension can be obtained, so we can only care about the horizontal coordinates.

Start and end points of a diagonal:

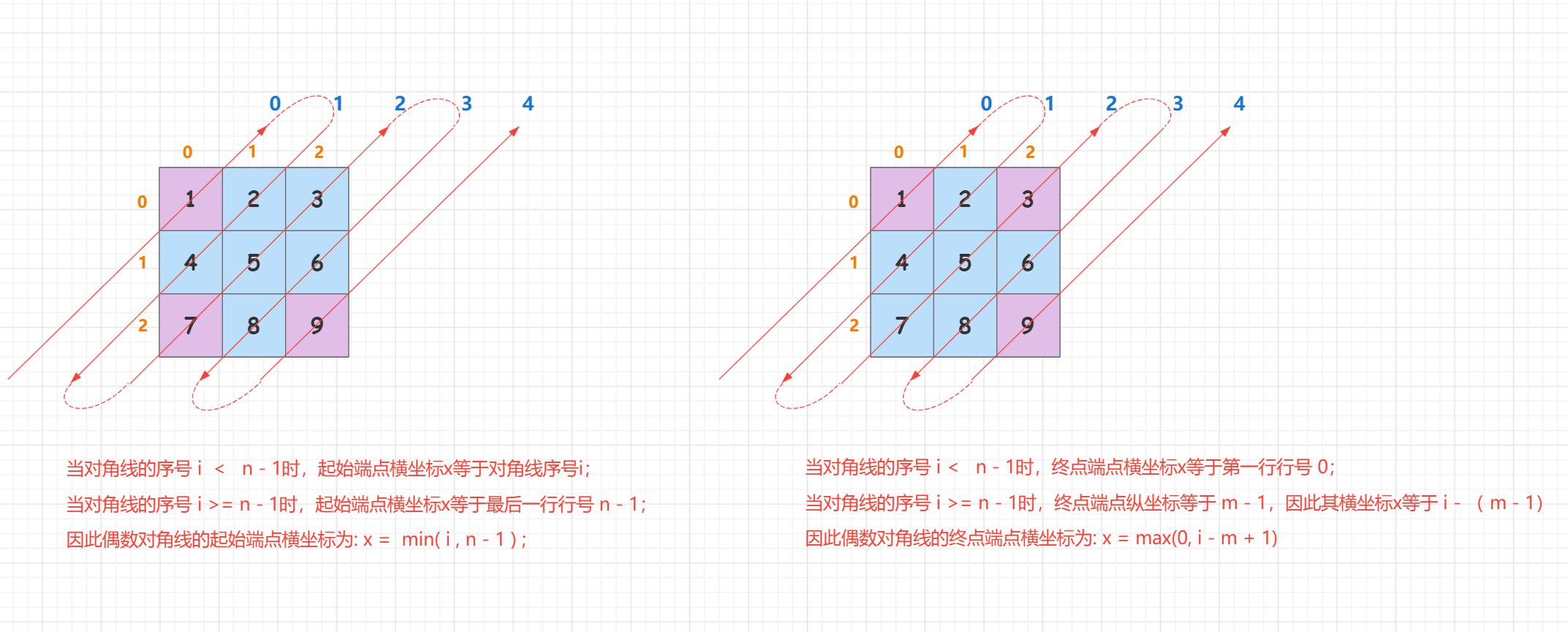
Thus, we determine that the horizontal coordinates of the start and end points of an even diagonal line are x = m i n (i, n - 1) and x = max(0, i - m + 1), respectively, and the vertical coordinates are i - x. (i is diagonal sequence number)

Odd diagonals are traversed i n the opposite direction to even diagonals, so the horizontal coordinates of the start and end points of odd diagonals are x = max(0, i - m + 1) and x = m i n (i, n - 1) and the vertical coordinates are i - x, respectively. (i is the diagonal serial number).

The next thought is clear, traversing each diagonal line. If it is an even number of diagonals, it traverses from bottom to top. If it is an odd diagonal, traverse from top to bottom.

The specific process is as follows:

• 1. Define the answer array res and traverse each diagonal line.

• 2. For each diagonal number i, determine its parity:

  • If it is an even diagonal line, determine its horizontal coordinate x, traverse from bottom to top, and add mat[x][i-x] to res.

  • If it is an odd diagonal, determine its horizontal coordinate x, traverse from top to bottom, and add mat[x][i-x] to res.

• 3. Return to res at last.

Time Complexity Analysis: O ( n ∗ m ) O(n*m) O(n_m), each element is processed only once.

3. c++ Code

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
        vector<int> res;
        if (mat.empty() || mat[0].empty()) return res;
        int n = mat.size(), m = mat[0].size();
        for (int i = 0; i < n + m - 1; i ++ ) 
        {
            if (i % 2 == 0)  //Even Diagonal
            {
                for (int x = min(i, n - 1); x >= max(0, i - m + 1); x -- )//Traverse from bottom to top
                    res.push_back(mat[x][i - x]);
            } else 		     //Odd Diagonal
            {      
                for (int x = max(0,  i - m + 1); x <= min(i, n - 1); x ++ )//Traverse from top to bottom
                    res.push_back(mat[x][i - x]);
            }
        }
        return res;
    }
};

4. java code

class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
    if (mat.length == 0 || mat[0].length == 0) return new int[0];
    int n = mat.length, m = mat[0].length;
    int[] res = new int[n * m];
    for (int i = 0, idx = 0; i < n + m - 1; i++) 
    {
        if (i % 2 == 0) //Even Diagonal
            for (int x = Math.min(i, n - 1); x >= Math.max(0, i - m + 1); x -- ) //Traverse from bottom to top
                res[idx++] = mat[x][i - x];
        else   		    //Odd Diagonal
            for (int x = Math.max(0, i - m + 1); x <= Math.min(i, n - 1); x ++ )//Traverse from top to bottom
                res[idx++] = mat[x][i - x];
    }
    return res;
  }
}

Topic link: 498. Diagonal traversal