Original link
https://leetcode.com/problems/unique-paths/
https://leetcode.com/problems/unique-paths-ii/
https://leetcode.com/problems/minimum-path-sum/
Solving problems
These three questions are similar, they all use dynamic programming.
Among them, unique path only needs to add the number of methods to each grid;

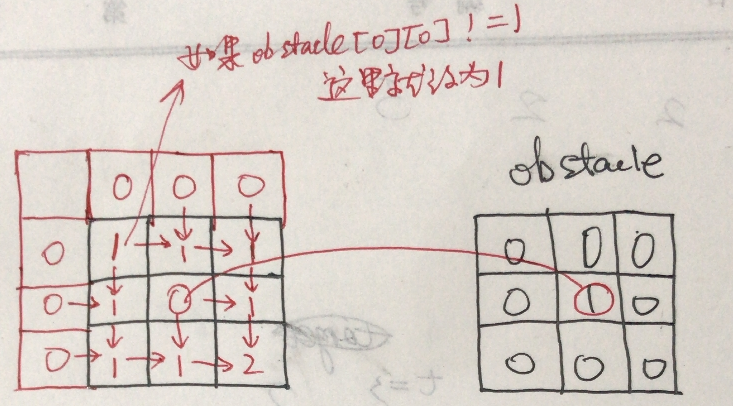
unique path II is a simple variant. Set the number of methods of the lattice with 1 in the obstacegrid to 0, and then add them according to the same method;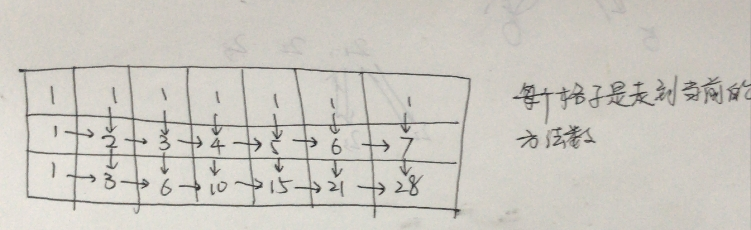

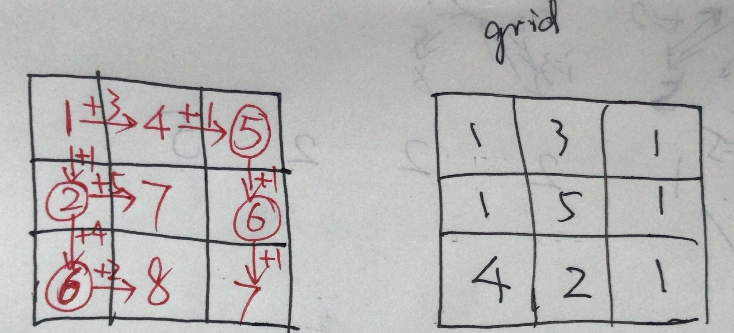
minimum path sum takes the smaller values in the upper and left squares and adds them to the addends in a given lattice to get the current minimum sum.

Code
unique path

class Solution():
    def uniquePaths(self, m, n):
        methods = [[1 for i in range(n)] for i in range(m)]
        for right in range(1, m):
            for down in range(1, n):
                methods[right][down] = methods[right-1][down] + methods[right][down-1]
        return methods[m-1][n-1]
        

unique path II

class Solution(object):
    def uniquePathsWithObstacles(self, obstacleGrid):
        """
        :type obstacleGrid: List[List[int]]
        :rtype: int
        """
        num_row = len(obstacleGrid) + 1
        num_col = len(obstacleGrid[0]) + 1

        expand_grid = [[0 for i in range(num_col)] for i in range(num_row)]

        for row in range(1, num_row):
            for col in range(1, num_col):
                if obstacleGrid[row-1][col-1]==1:
                    expand_grid[row][col] = 0
                elif row==1 and col==1:
                    expand_grid[row][col] = 1
                else:
                    expand_grid[row][col] = expand_grid[row][col-1] + expand_grid[row-1][col]
        return expand_grid[num_row-1][num_col-1]

minimum path sum

class Solution(object):
    def minPathSum(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        num_row = len(grid) + 1
        num_col = len(grid[0]) + 1
        sum_grid = [[0 for i in range(num_col)] for i in range(num_row)]
        for row in range(1, num_row):
            for col in range(1, num_col):
                if row==1:
                    sum_grid[row][col] = sum_grid[row][col-1] + grid[row-1][col-1]
                elif col==1:
                    sum_grid[row][col] = sum_grid[row-1][col] + grid[row-1][col-1]
                else:
                    sum_grid[row][col] = min(sum_grid[row-1][col], sum_grid[row][col-1]) + grid[row-1][col-1]
        return sum_grid[num_row-1][num_col-1]