In order from simple to difficult, break through the hurdles in turn (the title number is the serial number of leetcode)

Main JAVA

Source: https://leetcode-cn.com/

catalogue

1. Sum of two numbers (1) - hash table lookup

2. Delete duplicates in the ordered array (26) -- double pointers

3. Remove element (27) - Optimization of double pointer

4. Maximum subsequence sum (53) -- dynamic programming

5. The best time to buy and sell stocks (121) -- dynamic programming

6. The best time to buy and sell stocks II (122) -- dynamic programming

1. Sum of two numbers

Topic Description: given an integer array ， nums ， and an integer target value ， target, please find the ， and the ， integers with the target value ， target ， in the array, and return their array subscripts.

Problem solving ideas:

• Violence enumeration: find whether target-x exists in the array. The time complexity is o(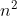), space complexity is O(1)
• Hash table: reduce the time complexity by quickly finding the target elements in the array and create a hash table. For each x, first query whether target-x exists in the hash table, and then insert x into the hash table to ensure that X does not match itself. Time complexity O(n), space complexity O(n)
  • Algorithm:
  1. Calculate the difference between the current number and the target number
  2. Whether the difference exists in the hash table is traversed. If so, the result is returned
  3. Does not exist. The current number is stored in the hash table as key and the index as value

• C

  struct hashTable{
      int key;
      int value;
      UT_hash_handle hh; //Using uthash
  };
  
  struct hashTable* ht;
  
  struct hashTable* find(int ikey){     //Find whether ikey exists in the hash table
      struct hashTable* tmp;
      HASH_FIND_INT(ht,&ikey,tmp);  //Find interface
      return tmp;
  }
  
  void insert(int ikey, int ivalue){   //Insert ikey into hash table
      struct hashTable* it = find(ikey); //Avoid repetition
      if(it == NULL){
          struct hashTable* tmp = malloc(sizeof(struct hashTable));  //Allocate space
          tmp->key = ikey;
          tmp->value = ivalue;
          HASH_ADD_INT(ht,key,tmp);  //Plug in interface
      }else{
          it->value = ivalue;  //cover
      }
  }
  
  int* twoSum(int* nums, int numsSize, int target, int* returnSize){
      ht = NULL; //New empty hash table
      for(int i = 0; i < numsSize; i++){
          struct hashTable* it = find(target - nums[i]);
          if(it != NULL){
              int* ret = malloc(sizeof(int) * 2);
              ret[0] = it->value;
              ret[1] = i;
              *returnSize=2;
              return ret;
          }
          insert(nums[i], i);
      }
      *returnSize = 0;
      return NULL;
  }

• JAVA

  class Solution {
      public int[] twoSum(int[] nums, int target) {
          Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>(); //HashMap object
          for(int i = 0; i < nums.length; i++){
              if(hashtable.containsKey(target-nums[i])){ //If target-x exists in the hash table
                  return new int[]{hashtable.get(target-nums[i]), i};
              }
              hashtable.put(nums[i],i); //insert
          }
          return new int[0];
      }
  }

• Python 3 (simulate hash table with dictionary)

  class Solution:
      def twoSum(self, nums: List[int], target: int) -> List[int]:
          hashtable = dict() #Simulate hash with dictionary
          for i, num in enumerate(nums):
              if target - num in hashtable:
                  return [hashtable[target-num], i]
              hashtable[nums[i]] = i
          return []

2. Delete duplicates in the ordered array

Title Description: give an ordered array {nums, delete the repeated elements in place, make each element appear only once, and return the new length of the deleted array. [Note: additional array space cannot be used]

Problem solving ideas:

• Double pointers: since the title is required to be modified in place and no additional array space is used, it is considered to use two pointers to delete and move elements. Set the two pointers as fast pointer and slow pointer respectively -- the fast pointer is used to traverse the array; The slow pointer is used to fill in the position of the next non duplicate item. The time complexity is O(n)
  • Algorithm:
  1. Initially, both fast and slow point to the subscript 1 (because it is an ordered array, the numbers with subscript 0 are not comparable, and can start from 1)
  2. Fast traverses each position from 1 to n-1 in turn. For each position, if num [fast] ≠ num [FAST-1], it indicates that the element is not duplicate with the previous one, and copy the value of num [fast] to num [slow]
  3. If and only if num [slow] is assigned, slow+1
  4. After fast traversal, return slow
• C (JAVA is similar to Python 3)

  int removeDuplicates(int* nums, int numsSize){
      //Handle special situations
      if(numsSize == 0){
          return 0;
      }
      int fast = 1;
      int slow = 1;
      while (fast < numsSize){  //ergodic
          if (nums[fast] != nums[fast-1]){  //Properties based on array ordering
              nums[slow] = nums[fast];
              slow++;
          }
          fast++;
      }
      return slow;
  }

3. Remove elements

Topic Description: given an array num ￠ and a value Val, it is required to remove all elements with a value equal to val ￠ in place and return the new length of the removed array. Do not use additional array space, the order of elements can be changed. There is no need to consider the elements in the array that exceed the new length

Problem solving ideas:

• Double pointer: similar to the idea of the previous question, set the double pointer to fast pointer and slow pointer respectively [traverse the sequence twice at most]
  • Algorithm:
  1. Initially, both fast and slow point to the subscript 0
  2. Fast traverses each position from 1 to n-1 in turn. For each position, if num [fast] ≠ val, copy the value of num [fast] to num [slow], slow+1
  3. If num [fast] = val, slow does not move, fast+1
  4. After fast traversal, return slow
• C (JAVA is similar to Python 3)

  int removeElement(int* nums, int numsSize, int val){
      int fast = 0;
      int slow = 0;
      for( ; fast < numsSize; fast++){
          if(nums[fast] != val){
              nums[slow] = nums[fast];
              slow++;
          }
      }
      return slow;
  }

• Optimization of double pointers: note that the [order of elements can be changed] in the title. Therefore, considering the small number of val elements in the sequence, only other elements need to be moved to replace val elements, which also meets the requirements of the title. Therefore, place two pointers at the beginning and end of the array and traverse the sequence in the middle. [traverse the sequence at most once]
• C (JAVA is similar to Python 3)

  int removeElement(int* nums, int numsSize, int val){
      int fast = numsSize;
      int slow = 0;
      while(slow < fast){
          if(nums[slow] == val){
              nums[slow] = nums[fast-1];
              fast--;
          }else{
              slow++;
          }
      }
      return slow;
  }

4. Maximum subsequence sum

Topic Description: given an integer array {nums, find a continuous sub array with the largest sum (the sub array contains at least one element) and return its maximum sum.

Problem solving ideas:

• Dynamic programming: Using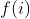Represented by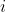The maximum sum of consecutive subarrays at the end of the number, so you need to find the sum of each position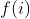, then return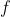The maximum value in the array. The point is how to find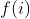——Considering whether nums[i] is a separate segment or f(i-1) is added, it depends on the size of nums[i] and f(i − 1)+nums[i], so the following dynamic programming transition equation can be written:

                                           

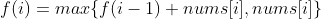
Space complexity O(n), time complexity O(n)

Note: since f(i) is only related to f(i-1), only one variable can be used to maintain the current values of f(i) and f(i-1), so as to reduce the spatial complexity to O(1)

• C

  int maxSubArray(int* nums, int numsSize){
      int value = 0; //Used to maintain the values of f(i) and f(i-1)
      int max = nums[0];  //Maximum
      for(int i=0; i < numsSize; i++){
          value = fmax(value +nums[i], nums[i]); //Find f(i)
          max = fmax(value, max);  //The maximum value is obtained by comparison in f(i)
      }
      return max;
  }

5. The best time to buy and sell stocks

Title Description: given an array of prices, its ＾ i-th element ＾ prices[i] represents the price of a given stock on day I. You can only choose to buy this stock on a certain day and sell it on a different day in the future. Design an algorithm to calculate the maximum profit you can make. Return the maximum profit you can make from this transaction. If you can't make any profit, return 0.

Solution idea: for each group I and J (where j > I), we need to find max (prices [J] - prices [i])

• Once traversal: buying stocks at the lowest point in history can ensure the maximization of benefits. Therefore, traverse the price array once, record the lowest point in history, and then compare the profits from selling on day I: prices[i] - minprice
• JAVA

  class Solution {
      public int maxProfit(int[] prices) {
          int minprices = Integer.MAX_VALUE; //Minimum profit set to maximum
          int maxprofit = 0;
          for(int i = 0; i <prices.length; i++){
              if(prices[i] < minprices){
                  minprices = prices[i];
              }else if(prices[i] - minprices > maxprofit){
                  maxprofit = prices[i] - minprices;
              }
          }
          return maxprofit;
      }
  }

Note: dynamic programming is used to solve multi-stage decision-making problems (grammar of dynamic programming problems: only the optimal solution, not the specific solution)

 6. The best time to buy and sell stocks II

Title Description: give an array of prices, where {prices[i] is the price of a given stock on day I. Design an algorithm to calculate the maximum profit you can make. You can complete as many transactions as possible (buy and sell a stock multiple times), but you can't participate in multiple transactions at the same time (you must sell the previous stock before buying again)

Problem solving ideas:

• Dynamic programming: because [cannot participate in multiple transactions at the same time], there may only be one stock or no stock in hand after the end of trading every day (first analyze the status). Define dp[i][0] as the maximum profit of no stock in hand after trading on day I, and dp[i][1] as the maximum profit of holding one stock after trading on day I

Considering the transfer equation of dp[i][0], you may hold a stock (dp[i-1][1]) and sell it before trading that day, or you may not have a stock (dp[i-1][0]). Therefore, the following transfer equation is listed:

          

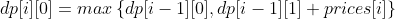
Consider the transfer equation of dp[i][1]: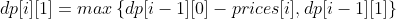

• JAVA

  class Solution {
      public int maxProfit(int[] prices) {
          int n = prices.length;
          int [][] dp = new int [n][2];
          //Or directly expressed by two variables
          //Define initial state:
          dp[0][0] = 0;
          dp[0][1] = -prices[0];
          for(int i=1; i<n; i++){
              dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
              dp[i][1] = Math.max(dp[i-1][0] - prices[i],dp[i-1][1]);
          }
          return dp[n-1][0]; //The stock held in the last hand is 0
      }
  }

• Greedy algorithm (only used to calculate the maximum profit, and the calculation process is not the actual transaction process): Based on the current situation, make the optimal selection according to an optimization measure (the solved problem is often mathematically modeled, divided into several subproblems, and each subproblem is solved to obtain the local optimal solution of the subproblem)

Since there is no limit to the number of stock purchases, the whole problem is equivalent to finding x disjoint intervals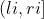Maximize the following equation: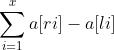(where li means buying and ri means selling)

At the same time, it was noted that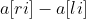It can be simplified to x intervals with length of 1 (li,li + 1)

From the perspective of greed, each selection of an interval with a contribution greater than 0 can maximize the answer. Therefore, the final answer is:

          

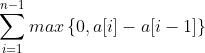
• JAVA

  class Solution {
      public int maxProfit(int[] prices) {
          int profit = 0;
          for(int i=1; i< prices.length; i++){
              profit = Math.max(0, prices[i] - prices[i-1]) + profit;
          }
          return profit;
      }
  }