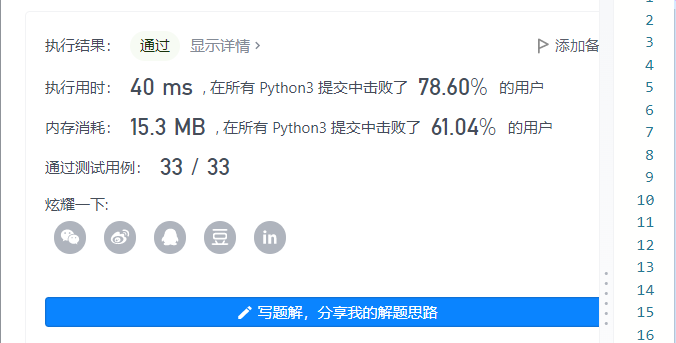
1, Review

First review the retrospective question written yesterday, and start with the simple one of full arrangement.
46. Full arrangement
In fact, this kind of backtracking is quite fun. Unlike dynamic programming, it can remember the details of answer, and all of them are on the path (we use continuous recursive path to record this value, and finally append the final answer to res).

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def dfs(path,res,nums):
            if len(nums)==0:
                res.append(path)
                return
            for i in nums:
                tmp_nums=[]
                for j in nums:
                    if j!=i:
                        tmp_nums.append(j)
                dfs(path+[i],res,tmp_nums)
            
        path=[]
        res=[]
        dfs(path,res,nums)
        return res

                

39. Combination sum

Write it yourself! Great!
There are three problems:
(1) after defining the recursive function, call the function and do not write it carelessly in the function.
(2) In order to avoid duplication with the previous sequence, the previously selected ones cannot be selected later. Therefore, index is set, and each branch can only be selected from its corresponding index. That is, you can choose the leftmost one. If you choose another online game, you can't choose the first one; You can't choose the second one. Gradually narrow the scope. Because there is no order, the leftmost is like a complete set, while the rightmost is like a set with only one element. Such branches are certainly not all possible cases, such as the smallest or medium single set, but in fact, the possibility of this set is also discussed earlier, which does not rule out that the smallest and medium are independent.
(3) In order to avoid being too complex, it involves pruning, so don't forget to sort!

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        def dfs(index,size,candidates,res,path,target):
            for i in range(index,size):
                residue = target-candidates[i]
                if residue<0:
                    break
                elif residue==0:
                    path+=[candidates[i]]
                    res.append(path)
                    return
                else:
                    dfs(i,size,candidates,res,path+[candidates[i]],residue)

        path=[]
        res=[]
        candidates.sort()
        dfs(0,len(candidates),candidates,res,path,target)
        return res

40. Combined sum II

1. At first, I forgot to ask for sort(), but there is another problem, which I omitted repeatedly

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        def dfs(index,size,res,path,target,candidates):
            if index==size:
                return
            for i in range(index,size):
                if i!=0 and candidates[i]==candidates[i-1]:
                    continue
                residue = target-candidates[i]
                if residue<0:
                    break
                elif residue==0:
                    res.append(path+[candidates[i]])
                    return
                else:
                    dfs(i+1,size,res,path+[candidates[i]],residue,candidates)
        res =[]
        path = []
        candidates.sort()
        dfs(0,len(candidates),res,path,target,candidates)
        return res

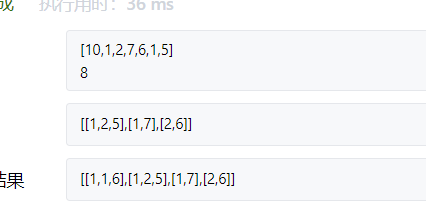
Note out the repeated problems

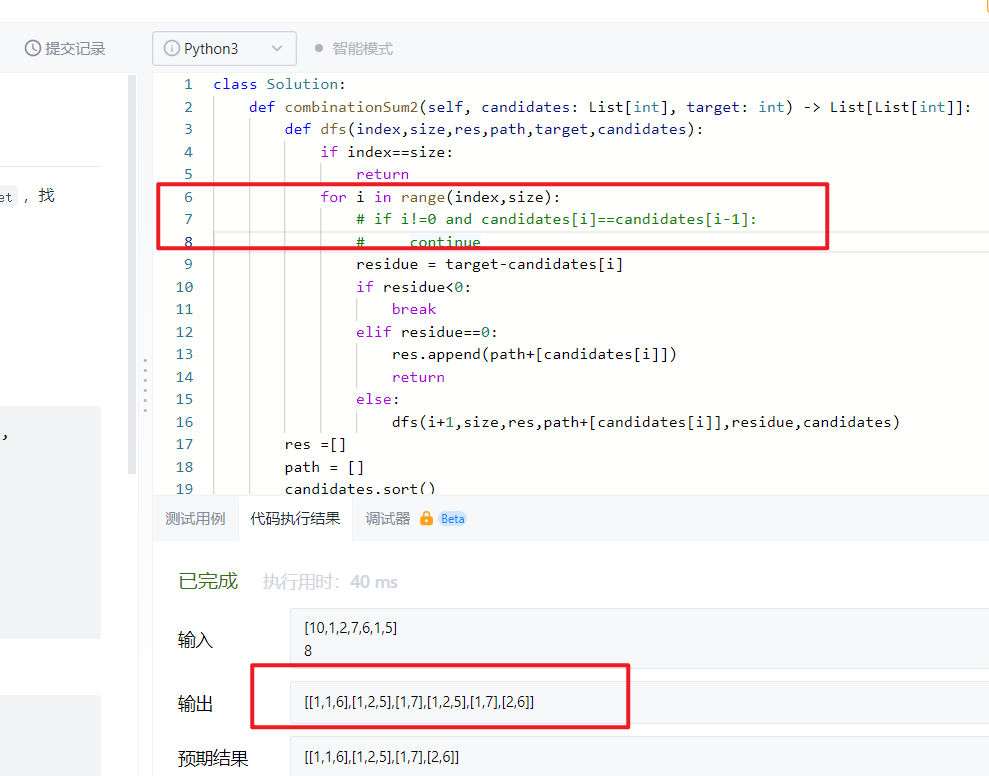
2. A judgment sentence is added: see whether this number already exists in the path. Because we allow vertical repetition, not horizontal repetition

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        def dfs(index,size,res,path,target,candidates):
            if index==size:
                return
            for i in range(index,size):
                if i!=0 and candidates[i]==candidates[i-1] and candidates[i] not in path:
                    continue
                residue = target-candidates[i]
                if residue<0:
                    break
                elif residue==0:
                    res.append(path+[candidates[i]])
                    return
                else:
                    dfs(i+1,size,res,path+[candidates[i]],residue,candidates)
        res =[]
        path = []
        candidates.sort()
        dfs(0,len(candidates),res,path,target,candidates)
        return res

3. It's time-out to redo directly. Let's see the answer
Gao Zan's method is as follows: call Juezi directly:
if i>index and candidates[i]==candidates[i-1]:
If it is not the first in a line (I > index) and there is a value equal to the previous value, that is, it has been discussed earlier, it will be ignored. If it is the first one in a line, it is equal to the previous value, which is equivalent to the next level branch. It can be retained. Whether it is the first one of the first layer is used to distinguish the true Jue Zi, and the judgment condition is I > index.

3, 47 Full arrangement II

Similar to question 40, it is simpler than question 40. It can't be horizontal (the result is repeated), but it can be vertical (because the array contains repeated values, which can be used for the corresponding number of times)

Forget sort again. If you do not sort, you cannot effectively exclude those repeated combinations, because those repeated combinations are not adjacent, and the judgment is invalid.

The more annoying part of this problem is the deleted elements of the array. If you delete it directly, there will be no elements before the traversal of num is completed, so you need to copy it out first. Note: after deletion, the overall size will change. When size=0, the path will be added and returned.

This question is similar to the previous one in judging whether to repeat horizontally or vertically.

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        def dsf(size, path, res, nums):
            for index in range(size):
                if index >0 and nums[index] == nums[index - 1]:
                    continue
                else:
                    tmp_num = []
                    for i in nums:
                        tmp_num.append(i)
                    new_path = tmp_num[index]
                    tmp_num.pop(index)
                    size = len(tmp_num)
                    if size==0:
                        res.append(path+[new_path])
                        return
                    dsf(size, path + [new_path], res, tmp_num)

        path = []
        res = []
        nums.sort()
        dsf(len(nums), path, res, nums)
        return res

3. See how others delete the elements in the list.
Using this slice nums[:i]+nums[i+1:] opens up a new memory space

I don't understand that it's overtime to change my to slice. Oh, the deletion operation failed. It should start with index+1. [whispering: how mentally retarded]

succeed! The deletion operation is realized by slicing. But I don't think the idea of this problem is clear. After all, the ~ goose stumbling in front of me will do it again tomorrow to sort out the idea.

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        def dsf(size, path, res, nums):
            for index in range(size):
                if index >0 and nums[index] == nums[index - 1]:
                    continue
                else:
                    new_path = nums[index]
                    tmp_num =nums[:index]+nums[index+1:]
                    size = len(tmp_num)
                    if size==0:
                        res.append(path+[new_path])
                        return
                    dsf(size, path + [new_path], res, tmp_num)

        path = []
        res = []
        nums.sort()
        dsf(len(nums), path, res, nums)
        return res