Title Content:

You are given two integer arrays nums1 and nums2 in non decreasing order, and two integers m and n representing the number of elements in nums1 and nums2 respectively. Please merge nums2 into nums1 so that the merged array is also arranged in non decreasing order.
Note: the final merged array should not be returned by the function, but stored in the array nums1. In order to deal with this situation, the initial length of nums1 is m + n, where the first m elements represent the elements that should be merged, and the last n elements are 0, which should be ignored. The length of nums2 is n.

leetcode title link (click to jump):

Train of thought analysis

After reading the title, we should not rush to program the title, but first carefully understand the meaning of the title. (some students may say at this time, "no, no, the content of the topic has been given, and no one can't understand it? No, no!" In fact, many partners may not seriously review the OJ question when they first start to work on it, but directly program it, report a lot of errors, debug them one by one, and finally... There is no end. It is really "from getting started to giving up ~". Therefore, in order to avoid this problem and practice more efficiently and correctly, we should "understand the topic - train of thought analysis (drawing understanding) - extreme scene - hands-on programming - Review and summary". These steps seem cumbersome, but in fact, they take less time than direct programming, and the final learning and practice effect is much better.

(of course, sharing blogs can also help us sort out our ideas and summarize our experience and methods. The most important thing is to help others. However, the process of brushing questions has more "other meanings")

So the problem comes, how to better understand the problem?
(1) After reading the title, retell it in your own words, just with the same general meaning.

For example, this topic, The general meaning of the title is "there are two overall ascending order" (that is, there may be equal elements in the middle, not strictly ascending order, which is the understanding of "non decreasing arrangement") Array num1, num2. Num1 has m elements, but the length is m+n, num2 has n elements, and the length is n. Now we are required to combine the two arrays into one array and store it in num1. The sorting method is the same as before. "

(2) Ask yourself questions from multiple perspectives

for instance:
① Does the title require that temporary arrays cannot be opened? In other words, the spatial complexity is required to be O(1), or the data is processed in situ. (obviously, this question does not have this requirement!)
② Does the title say that m and n cannot be equal to 0? What should I do if it is equal to 0?
③ Are there any requirements for time complexity in the topic? (the time complexity required for the advanced part is O(n+m)

Method 1: temporary array method

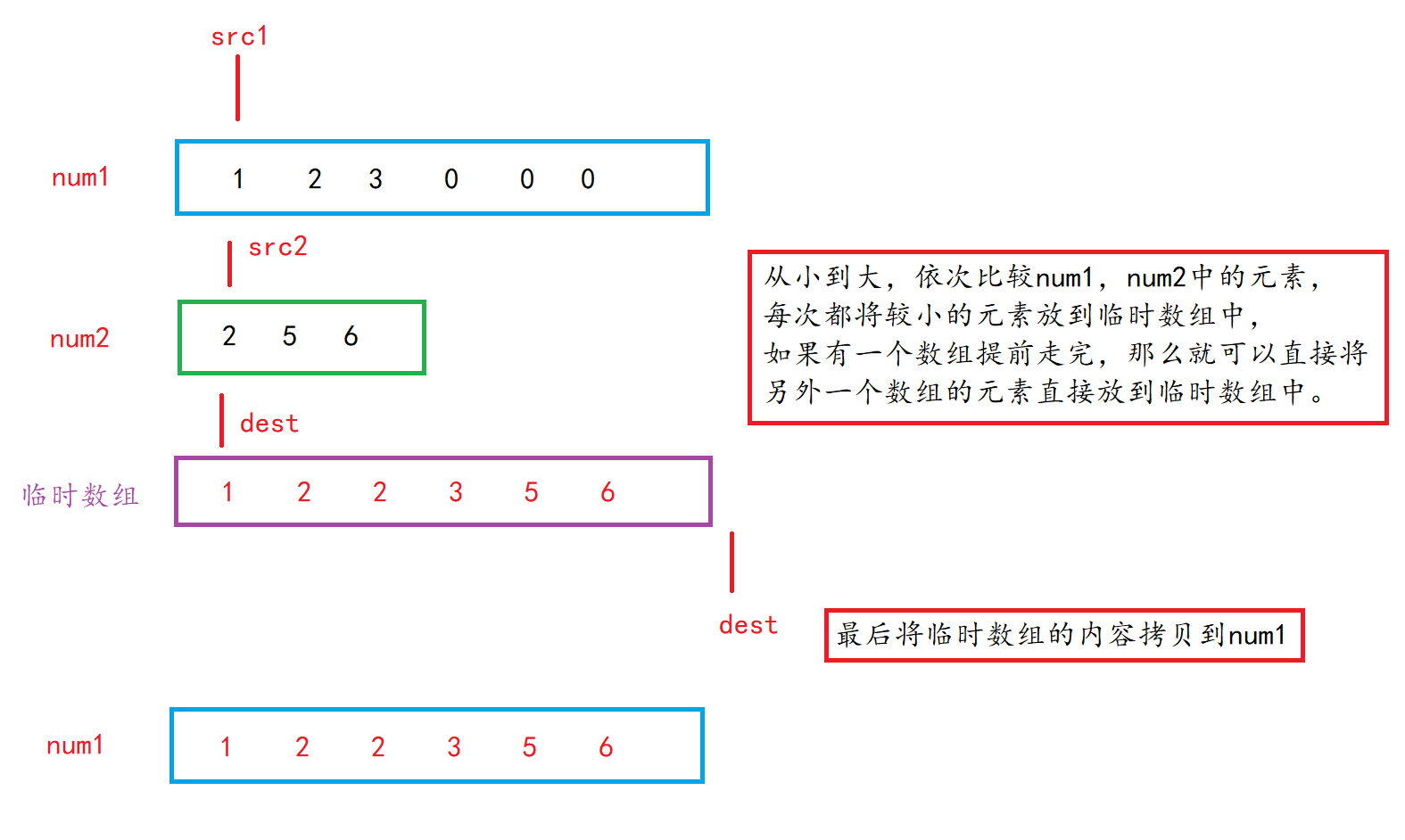
Since the title does not require "in situ" merging of data, it should be easy for us to think of establishing a temporary array with a length of n+m. first, put the contents of num1 and num2 into the temporary array in a "non descending" manner, and then copy the contents of the temporary array back to num1 array.
In this way, for the situation of topic ②:

1) m=0, n=0 do not conform to 1 in the topic prompt<=
m+n. (in fact, I'm a little curious about how to deal with m=n=0 and m+n=0. Can you create a temporary array with a length of 0? Is an array with a length of 0 meaningful? When m=0, it just means that there are no valid elements in num1, but the actual length is not m, but n + m > = 1. If you do, you don't need to open a temporary array and deal with it directly)
2) m=0, n > 0, that is, there are no valid elements in num1, and there are n valid elements in num2. At this time, all the data in num2 will be put into the temporary array first, and then copied from the array to num1, which can solve the problem without errors (although the efficiency is a little low, the problem is solved anyway, the problem is not big)
3) n=0, M > 0, that is, there are no valid elements in num2, and there are m valid elements in num1. At this time, all the data in num1 will be put into the temporary array, and then copied from the array to num1, which can solve the problem without errors. (well, it looks dull)

Therefore, on the whole, the temporary array method will not have too many problems. At this time, you can draw diagrams and write code tests.

Algorithm diagram

Function interface implementation

void merge(int* nums1, int nums1Size, int m, 
int* nums2, int nums2Size, int n){
    int* arr = (int*)malloc((m+n)*sizeof(int));//Create a temporary variable of length m+n
    int src1 = 0;//Starting subscript of nums1
    int src2 = 0;//Initial subscript of nums2
    int dest = 0;//Starting subscript of arr
    while((src1 < m) && (src2 < n)){
        if(nums1[src1] <= nums2[src2]){
            //Assign the element of nums1 to arr, and the subscripts of the two arrays move backward at the same time
            arr[dest++] = nums1[src1++];
        }
        else{
            //Assign the element of nums2 to arr, and the subscripts of the two arrays move backward at the same time
            arr[dest++] = nums2[src2++];
        }
    }
    //This means that one of num1 or num2 is over
    if(src1 == m){
        //src1 = m means that all valid elements in num1 have been moved to arr
        //You only need to move all elements in arr 2
        while(src2 < n){
            arr[dest++] = nums2[src2++];
        }
    }
    else{
        //src2 = n indicates that all valid elements in num2 have been moved to arr
        //Just move all the elements in num1 to arr
        while(src1 < m){
            arr[dest++] = nums1[src1++];
        }
    }
    //Finally, copy the elements in arr to num1
    for(int i = 0; i < (n+m); i++){
        nums1[i] = arr[i];
    }
    //Release dynamic array
    free(arr);
    arr = NULL;
}

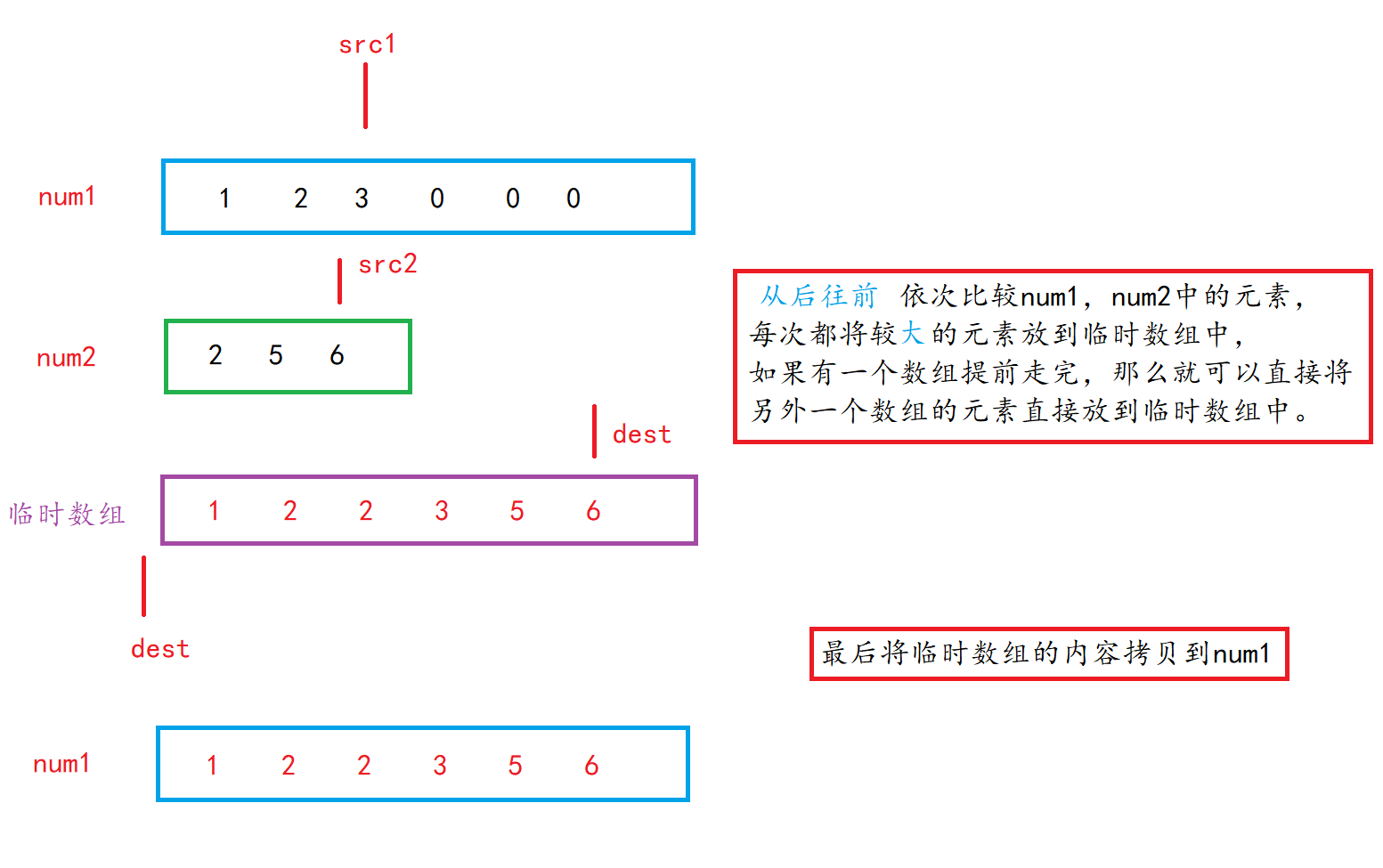
In the above method of using temporary arrays, when we move the elements in num1 and num2 to the temporary array, we use the method from the beginning to the end of num1 and num2 arrays, that is, we use the "front to back" method. So can we adopt the "back to front" approach? (since I have asked, I naturally can't "talk without doing fake tricks")

Method 2: temporary array inverted version

(don't ask why it's called the inverted version, why it's not called the inverted version, the reverse version and the reverse version??? I feel that the word "inverted version" is more "domineering", yes, it's more "domineering", and there's a feeling of "domineering exposure" when there's wood?)
This method only needs to make some adjustments on the basis of the original temporary array method. It mainly changes the two subscripts src1 and src2 from the previous "front to back" to "back to front". When comparing the two, whoever is large will be retained in the temporary array arr. note that the temporary array also needs to be traversed from back to front.

Algorithm diagram

Function interface implementation

void merge(int* nums1, int nums1Size, int m, 
int* nums2, int nums2Size, int n){
    int* arr = (int*)malloc((m+n)*sizeof(int));//Create a temporary variable of length m+n
    int src1 = m - 1;//Termination subscript of nums1
    int src2 = n - 1;//Termination subscript of nums2
    int dest = m + n - 1;//Termination subscript of arr
    while((src1 >= 0) && (src2 >= 0)){
        if(nums1[src1] >= nums2[src2]){
            //Assign the element of nums1 to arr, and the subscripts of the two arrays move forward at the same time
            arr[dest--] = nums1[src1--];
        }
        else{
            //Assign the element of nums2 to arr, and the subscripts of the two arrays move forward at the same time
            arr[dest--] = nums2[src2--];
        }
    }
    //This means that one of num1 or num2 is over
    if(src1 < 0){
        //SRC1 < 0 means that all valid elements in num1 have been moved to arr
        //Just move all the elements in num2 to arr
        while(src2 >= 0){
            arr[dest--] = nums2[src2--];
        }
    }
    else{
        //Src2 < 0 means that all valid elements in num2 have been moved to arr
        //Just move all the elements in num1 to arr
        while(src1 >= 0){
            arr[dest--] = nums1[src1--];
        }
    }
    //Finally, copy the elements in arr to num1
    for(int i = 0; i < (n+m); i++){
        nums1[i] = arr[i];
    }
    //Release dynamic array
    free(arr);
    arr = NULL;
}

Although the temporary array method can solve the problem, we assume that "the two arrays to be merged are very large, that is, m+n is very large", then the larger the space of the temporary array we need to create, and the space complexity is O(n+m). The time complexity of the above two temporary array methods is O(n+m), that is, they meet the requirements of the advanced version.
Articles on time complexity and space complexity:
[data structure learning notes] I. Introduction to data structure and algorithm analysis (Advanced Guide for beginners)
So is there a way not only to open up temporary arrays, but also to achieve the effect similar to temporary arrays? (that is, the time complexity remains unchanged, which is O(n+m), but the spatial complexity becomes O(1))
The answer, of course, is "yes!", I would like to call this method "super advanced version, luxury advanced version and ultimate plus version". At least at present, I can't find an algorithm more efficient than this method.

Method 3: virtual array method (super luxury ultimate puls version)

This method can be said to be developed from the "inverted version of temporary arrays" (at least I think so). In the inverted version, the two arrays traverse from back to front to save the larger number into the temporary array. In fact, you don't have to put it in the temporary array, but you can put it directly in num1. Because the length of num1 itself is enough (m+n) and the N positions behind num1 do not put valid data, there is no need to worry about the data being overwritten. (if you want to traverse from front to back, you need to worry about overwriting the data in the original num1) finally, the step of copying the contents of the temporary array back to num1 can be omitted. (there should be "666, Nb, my God!")

Algorithm diagram

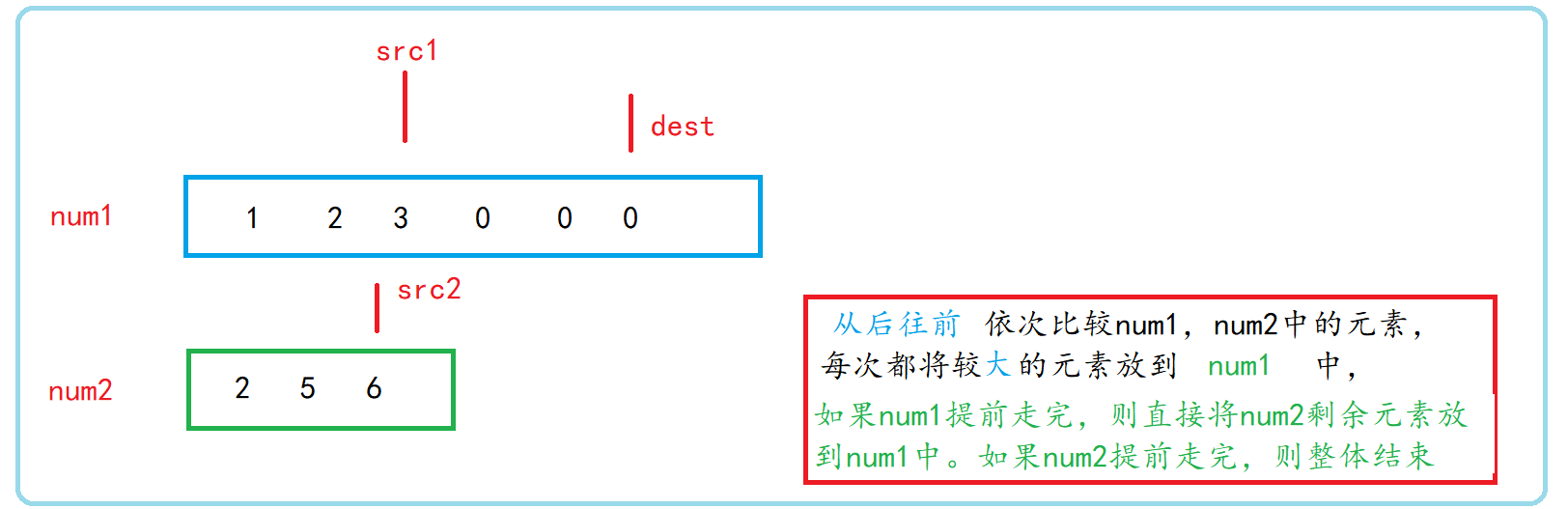
Function interface implementation

void merge(int* nums1, int nums1Size, int m, 
int* nums2, int nums2Size, int n){
    int src1 = m - 1;//Termination subscript of valid elements of array nums1
    int src2 = n - 1;//Terminating subscript of array nums2
    int dest = m + n - 1;//Termination subscript of array nums1 as a whole
    while(src1 >= 0 && src2 >=0){
        if(nums1[src1] >= nums2[src2]){
            //Assign the element pointed to by src1 of nums1 to the position pointed to by dest of nums1
            //Both array subscripts move forward at the same time
            nums1[dest--] = nums1[src1--];
        }
        else{
            //Assign the element pointed to by src2 of nums2 to the position pointed to by dest of nums1
            //Both array subscripts move forward at the same time
            nums1[dest--] = nums2[src2--];
        }
    }
    //Coming here means that src1 or src2 is over
    if(src1 < 0){
        //If src1 is completed in advance, copy all the elements in nums2 to nums1
        while(src2 >= 0){
            nums1[dest--] = nums2[src2--];
        }
    }
    //If src2 is completed in advance, no processing is required
}

It's not easy to be original. Let's praise, comment and note~
Your support will be the biggest driving force for me to move forward!!!