1. Populates the next right node pointer for each node
   Given a perfect binary tree, all leaf nodes are in the same layer, and each parent node has two child nodes. Binary tree is defined as follows:

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Fill in each of its next pointers so that this pointer points to its next right node. If the next right node cannot be found, set the next pointer to NULL.

In the initial state, all next pointers are set to NULL.

Advanced:

You can only use constant level extra space.
Using recursion to solve the problem also meets the requirements. The stack space occupied by the recursive program in this problem is not considered as additional space complexity.

Example:

Input: root = [1,2,3,4,5,6,7]
Output: [1, #, 2,3, #, 4,5,6,7, #]
Explanation: given A binary tree, as shown in figure A, your function should fill in each next pointer to point to its next right node, as shown in Figure B. The serialized output is arranged by sequence traversal, and the nodes of the same layer are connected by the next pointer,'# 'marks the end of each layer.

Tips:

The number of nodes in the tree is less than 4096
-1000 <= node.val <= 1000

Method 2: use the established next pointer
thinking

There are two types of next pointers in a tree.

The first case is to connect two children of the same parent node. They can be accessed directly through the same node, so you can complete the connection by performing the following operations.

node.left.next = node.right

In the second case, a connection is established between the child nodes of different fathers, which cannot be connected directly.

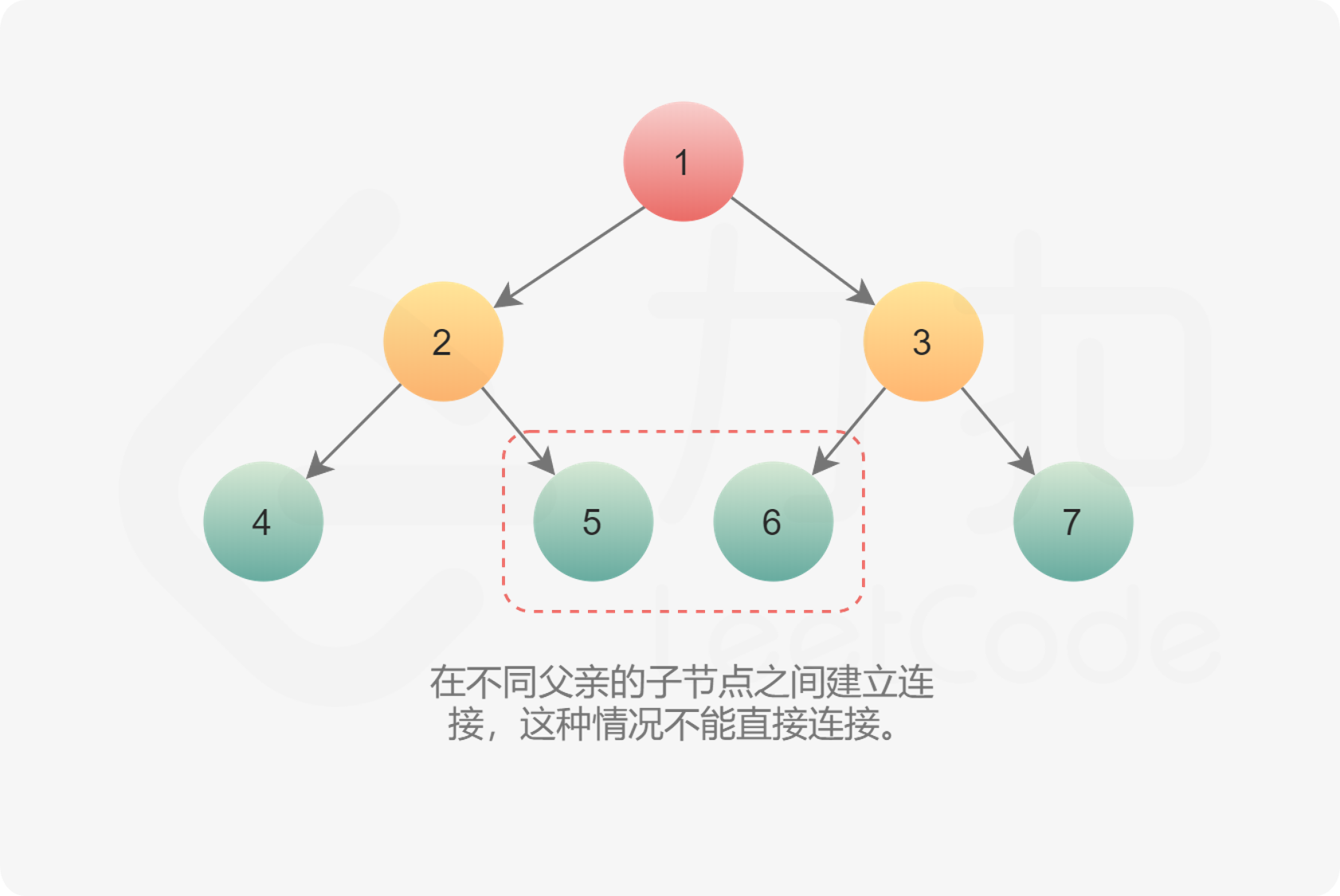
If each node has a pointer to the parent node, you can find the next node through the pointer. If the pointer does not exist, establish the connection according to the following idea:

After the next pointer is established between the nodes of layer N, the next pointer of the nodes of layer N+1 is established. All nodes of the same layer can be accessed through the next pointer. Therefore, the next pointer of layer N can be used to establish the next pointer for the nodes of layer N+1.

algorithm

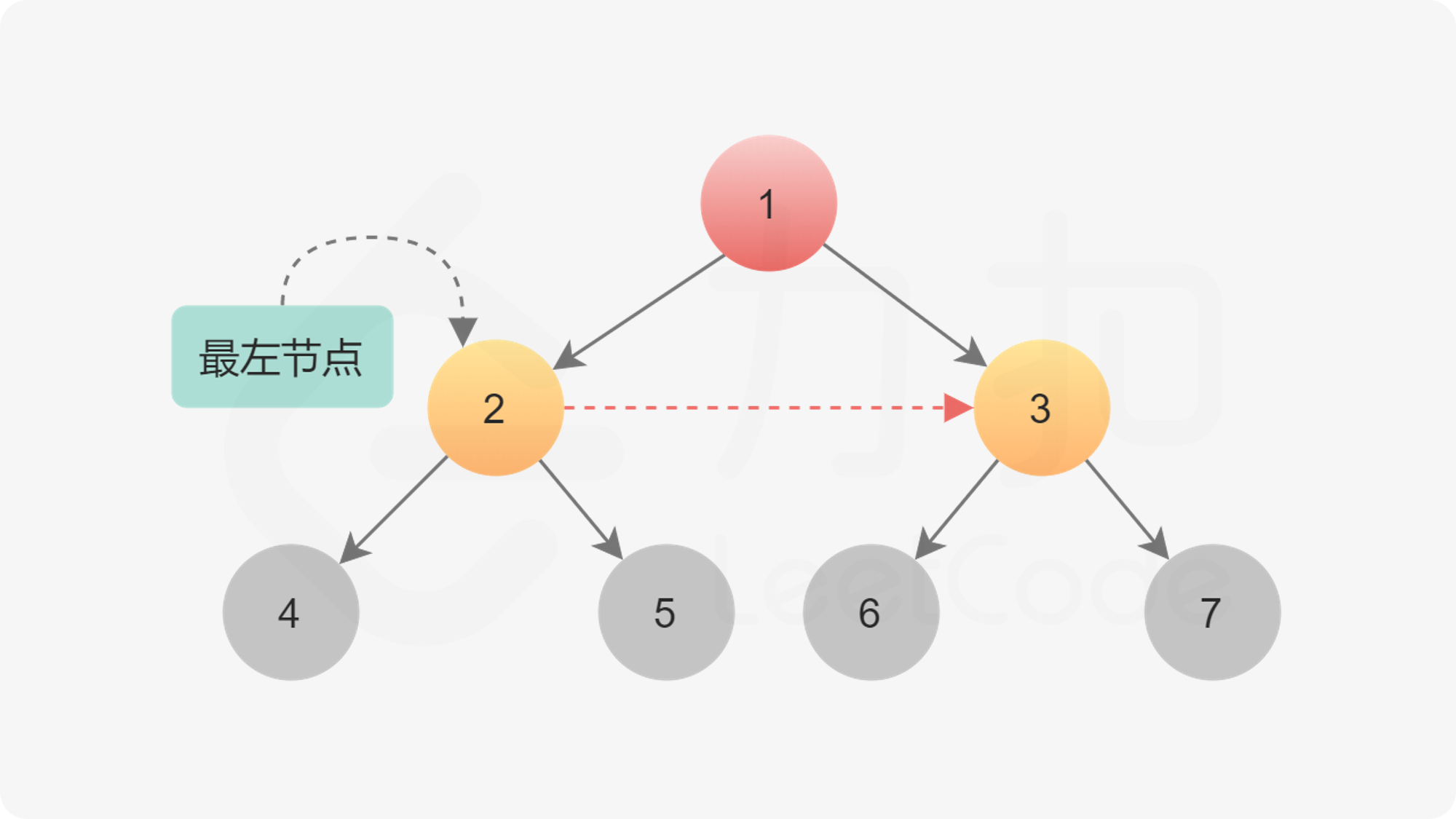
Starting from the root node, there is only one node in layer 0, so there is no need to connect. You can directly establish the next pointer for the node in layer 1. One thing to note in the algorithm is that when we establish the next pointer for the node at layer N, it is at layer N − 1. When all the next pointers of the node at layer N are established, move to layer N to establish the next pointer of the node at layer N+1.

When traversing a node of a layer, the next pointer of the node of this layer has been established. Therefore, we only need to know the leftmost node of this layer, and we can traverse it in a linked list without using a queue.

The pseudo code of the above idea is as follows:

leftmost = root
while (leftmost.left != null) {
    head = leftmost
    while (head.next != null) {
        1) Establish Connection 1
        2) Establish Connection 2 using next pointers
        head = head.next
    }
    leftmost = leftmost.left
}

There are two types of next pointers.

In the first case, two child nodes belong to the same parent node, so you can directly establish the next pointer of two child nodes through the parent node.

node.left.next = node.right

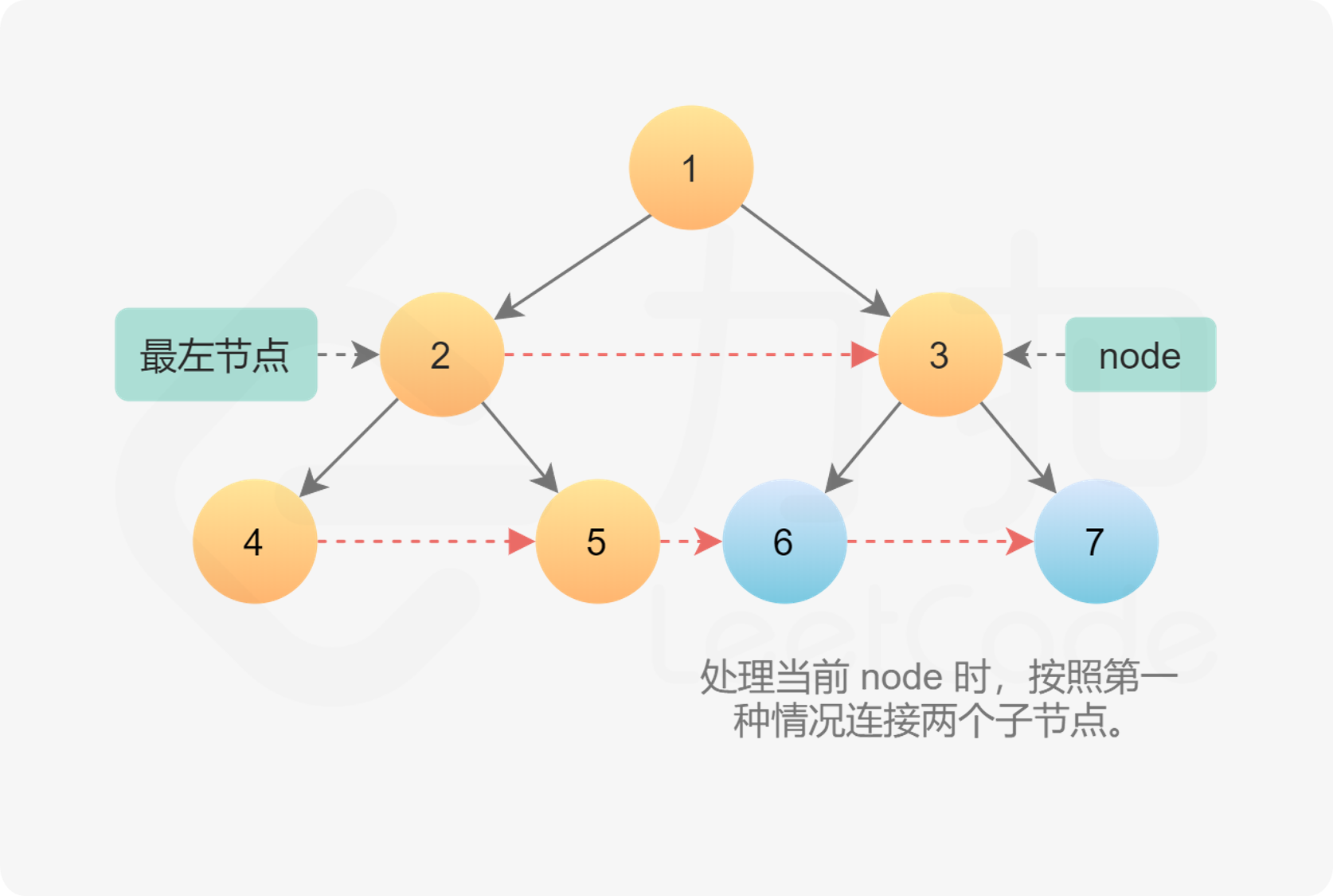
The second case is the case of connecting child nodes between different parent nodes. More specifically, the right child of the first parent node and the left child of the second parent node are connected. Since the next pointer has been established at the parent node level, you can directly find the second parent node through the next pointer of the first parent node, and then establish a connection between their children.

node.right.next = node.next.left

After completing the connection of the current layer, enter the next layer and repeat the operation until all nodes are connected. After entering the next layer, you need to update the leftmost node, and then traverse all nodes of the layer from the new leftmost node. Because it is a perfect binary tree, the leftmost node must be the left child of the leftmost node of the current layer. If the left child of the current leftmost node does not exist, it indicates that it has reached the last layer of the tree and completed the connection of all nodes.

Author: leetcode solution
Link: https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/solution/tian-chong-mei-ge-jie-dian-de-xia-yi-ge-you-ce-2-4/

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        if (root == nullptr) return nullptr;

        Node* leftmost = root;

        while (leftmost->left != nullptr) {
            Node* head = leftmost;

            while (head != nullptr) {
                head->left->next = head->right;
            
                if (head->next != nullptr)
                    head->right->next = head->next->left;

                head = head->next;
            }

            leftmost = leftmost->left;
        }

        return root;
    }
};