1. DFS basic framework
DFS in Figure
The core issue is "Traversing a two-dimensional array"
The two-dimensional array traversal framework is as follows:
void dfs (int[][] grid , int i , int j , boolean[] visited) {
int m = gird.length , n = grid[0].length;
//Check for out of bounds
if (i < 0 || j < 0 || i >= m || j >= n) {
//Index boundary exceeded
return ;
}
//Check whether the node has been accessed or exclude irrelevant nodes in the topic
if (visited[i][j] || grid[i][j] != ... ) {
return ;
}
//access node
visited[i][j] = true;
//"Infection"
grid[i][j] = ... ;
dfs(grid,i+1,j,visited); //upper
dfs(grid,i-1,j,visited); //lower
dfs(grid,i,j-1,visited); //Left
dfs(grid,i,j+1,visited); //right
}
//Small tips: you can use "direction array" to traverse up, down, left and right
int[][] dirs = new int[][]{ {-1,0} , {1,0} , {0,-1} , {0,1} };
//Recursive traversal of upper, lower, left and right nodes
for (int[] d : dirs) {
int next_i = i + d[0];
int next_j = j + d[1];
dfs(grid , next_i , next_j , visited);
}
DFS in tree
Compared with the figure, it is much simpler and does not need to judge whether to access repeatedly
int dfs (TreeNode root , ...) {
//Check whether the end is reached
if (root == null) {
return ...;
}
//Check some special situations of left and right children
if (root.left ... && root.right ... ) {
return ...;
}
//access node
Update related variables
//"Infection" can be transmitted to left and right children
return ...
dfs(root.left,...);
dfs(root.right,...
}
2. LeetCode related examples
(1) Flood Fill algorithm (island problem)
LC 733 image rendering (paint bucket tool)
LeetCode 733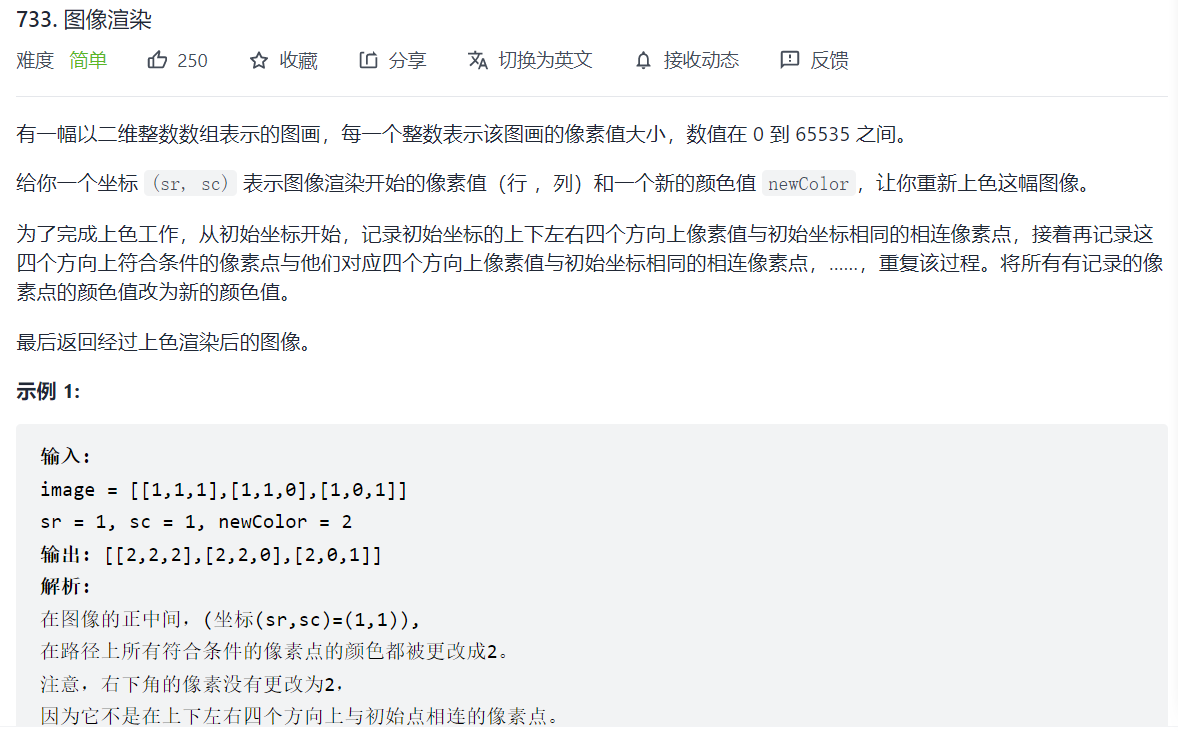 
The function to be realized is similar to the "paint bucket tool" in PS
Just follow the template directly
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
//If the color to be adjusted does not change, return directly
if(image[sr][sc]==newColor)
return image;
dfs(image,sr,sc,image[sr][sc],newColor);
return image;
}
//dfs
public void dfs(int[][] image,int x,int y,int oldColor,int newColor){
//Coordinate out of bounds and different colors
if(x<0 || x>=image.length || y<0 || y>=image[0].length || image[x][y]!=oldColor){
return ;
}
image[x][y] = newColor; //Coloring
dfs(image,x+1,y,oldColor,newColor);
dfs(image,x-1,y,oldColor,newColor);
dfs(image,x,y+1,oldColor,newColor);
dfs(image,x,y-1,oldColor,newColor);
}
}
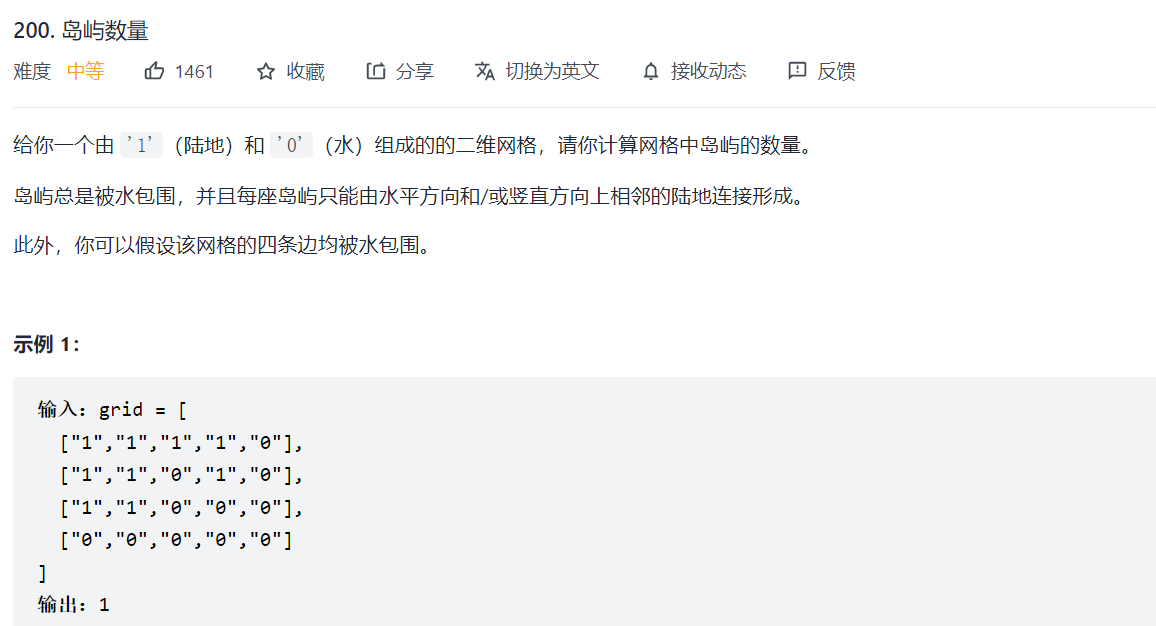
LC 200 number of islands
It can be associated with "dyeing". That is to dye a certain block (an island), and the question is how many blocks (islands)? What is the role of DFS in this question?
It is still "staining", but to be precise, it is "flooding the island" to avoid repeated counting
First traversing search, find a region for 1 (land) count +1, and then call DFS to submerge the island.
class Solution {
public int numIslands(char[][] grid) {
int res = 0; //Number of islands
for (int i = 0; i < grid.length;i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1') { //Found one
res++;
dfs(grid,i,j); //Flooded the island
}
}
}
return res;
}
//Flooded the island with dfs
public void dfs (char[][] grid , int i , int j) {
//Detect whether it is out of bounds
if (i < 0 || j < 0 || i >= grid.length || j >= grid[0].length)
return;
//Is the island detected
if (grid[i][j] != '1')
return;
//flooded
grid[i][j] = '0';
dfs(grid , i+1 , j);
dfs(grid , i-1 , j);
dfs(grid , i , j+1);
dfs(grid , i , j-1);
}
}
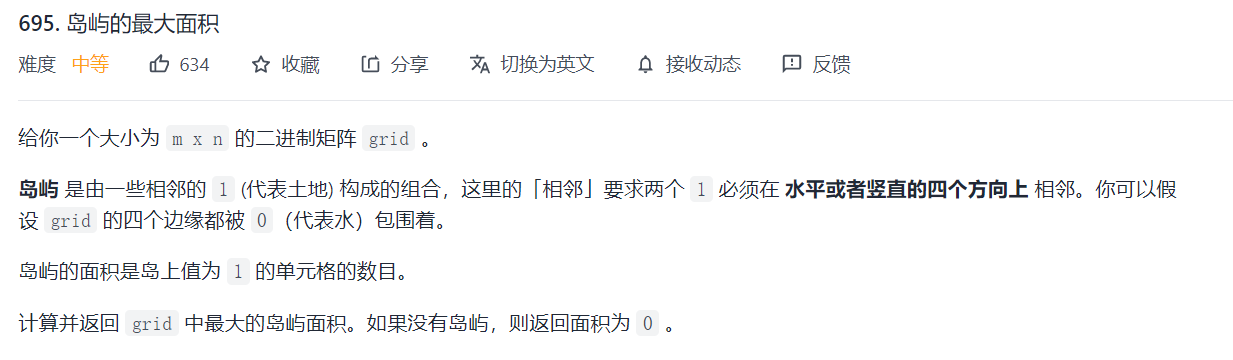
Maximum area of LC 695 Island
Similar to the previous question
It's just to ask for the area when the island is flooded
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int res = 0; //Record maximum area
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
res = Math.max(res,dfs(grid,i,j));
}
}
}
return res;
}
//Flood the island while returning to the area of the island
public int dfs (int[][] grid , int i, int j) {
//Detection boundary value
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length)
return 0;
//Out of the boundary of the island
if (grid[i][j] == 0)
return 0;
//flooded
grid[i][j] = 0;
return dfs(grid,i-1,j)
+ dfs(grid,i+1,j)
+ dfs(grid,i,j+1)
+ dfs(grid,i,j-1) + 1;
}
}
Number of LC 1020 enclaves
LeetCode 1020
The essence is to seek a "closed island", which requires a "real island" surrounded by water
That is to flood the islands around (up, down, left and right), and then count the rest
//Flooded the surrounding
for (int j = 0; j < grid[0].length; j++) {
dfs(grid,0,j); //Submerged upper
dfs(grid,grid.length-1,j); //Submerged
}
for (int i = 0; i < grid.length; i++) {
dfs(grid,i,0); //On the left
dfs(grid,i,grid[0].length-1); //On the right
}
After that, it will operate normally. If the number of "closed islands" is required, the islands will be flooded one by one
If the area of "closed island" is required, the size of the island shall be compared while flooding the island
In this problem, the total area of all "closed islands" is calculated, so there is no need to flood the island, and you can traverse it directly
The complete code is as follows:
class Solution {
public int numEnclaves(int[][] grid) {
int res = 0;
//Flood the islands on four sides first
for (int j = 0; j < grid[0].length; j++) {
dfs(grid,0,j); //Submerged upper
dfs(grid,grid.length-1,j); //Submerged
}
for (int i = 0; i < grid.length; i++) {
dfs(grid,i,0); //On the left
dfs(grid,i,grid[0].length-1); //On the right
}
//Count the number of remaining islands
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
res++;
//dfs(grid,i,j);
}
}
}
return res;
}
public void dfs(int[][] grid, int i, int j) {
//Detect whether it is out of bounds
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length)
return;
//Boundary detected
if (grid[i][j] == 0)
return;
//Flooded Island
grid[i][j] = 0;
dfs(grid,i+1,j);
dfs(grid,i-1,j);
dfs(grid,i,j+1);
dfs(grid,i,j-1);
}
}
LC 1034 boundary coloring
LeetCode 1034
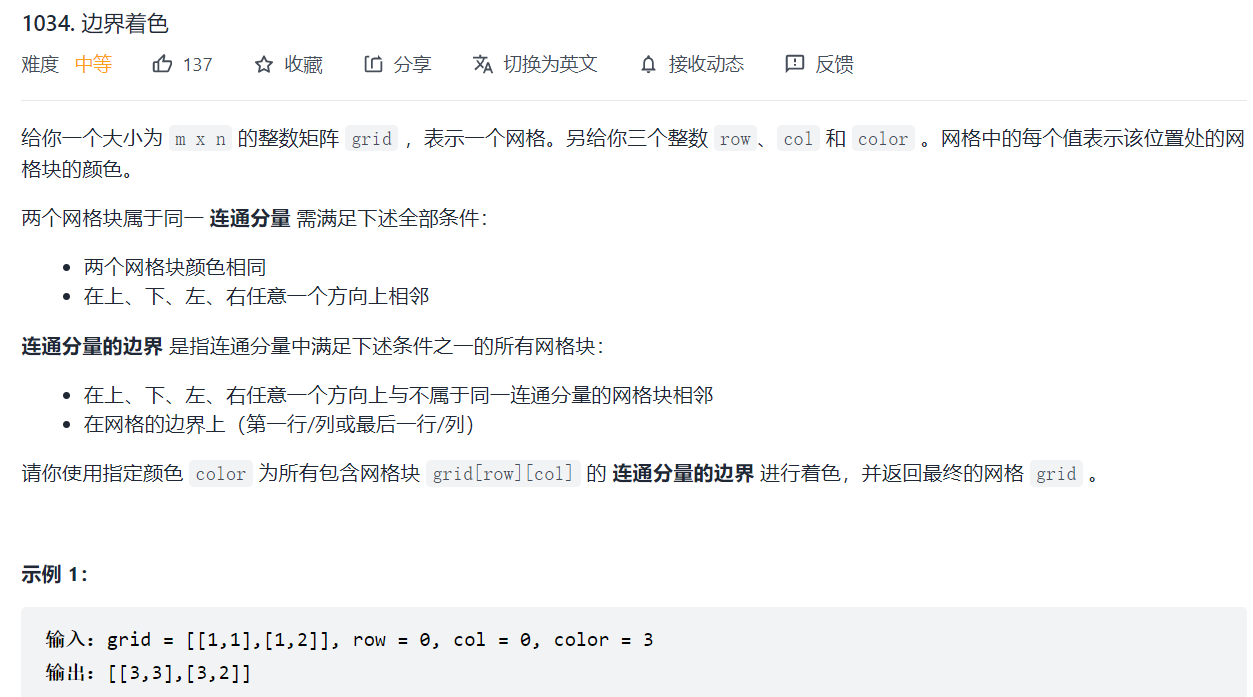
First understand the meaning of the question:
Connected component: refers to the collection of grids (i.e. adjacent grids) with the same color in one of the four directions up, down, left and right
Boundary coloring: the grid next to other colors or the grid next to the matrix boundary in the connected components pointed to by the coordinates of row and col is called boundary, and these boundaries are colored.
Consistent with the idea of DFS inundating islands:
The connected component is equivalent to an island
Coloring the connected component is equivalent to flooding the island (the problem requires coloring the boundary of the connected component)
Basic ideas:
The same is the idea of drowning the island
(1) First, color the connected components as a whole
(2) traverse again ,Restore the internal elements to the original color to achieve the effect of boundary coloring
How to determine whether it is an internal element?
The surrounding elements have been visited
if (visited[i][j] && visited[i+1][j] && visited[i-1][j] && visited[i][j-1] && visited[i][j+1]) {...}
class Solution {
public:
vector<vector<int>> colorBorder(vector<vector<int>>& grid, int row, int col, int color) {
if (grid[row][col] == color)
return grid;
int oldColor = grid[row][col];
vector<vector<bool>> visited(grid.size(),vector(grid[0].size(),false));
dfs(grid,row,col,oldColor,color,visited); //Find the connected component first
//Find the boundary value in the connected component
for (int i = 1; i < grid.size() - 1; i++) {
for (int j = 1; j < grid[0].size() - 1; j++) {
// Look for the inner point and dye the inner point back
if (visited[i][j] && visited[i+1][j] && visited[i-1][j] && visited[i][j-1] && visited[i][j+1]) {
grid[i][j] = oldColor;
}
}
}
return grid;
}
//Basic idea:
//First round: dfs is similar to the island flooding the connected component
//The second round: traverse again, find the internal points and dye them back
void dfs(vector<vector<int>>& grid , int i , int j , int oldColor , int newColor,vector<vector<bool>>& visited) {
//Boundary value judgment
if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size())
return ;
//Judge whether it has reached the boundary
if (grid[i][j] != oldColor)
return ;
//Finding "rules of connected components" in four directions
visited[i][j] = true; //Mark the flooded connected component
grid[i][j] = newColor;
dfs(grid,i+1,j,oldColor,newColor,visited);
dfs(grid,i-1,j,oldColor,newColor,visited);
dfs(grid,i,j+1,oldColor,newColor,visited);
dfs(grid,i,j-1,oldColor,newColor,visited);
}
};
(2) Search application
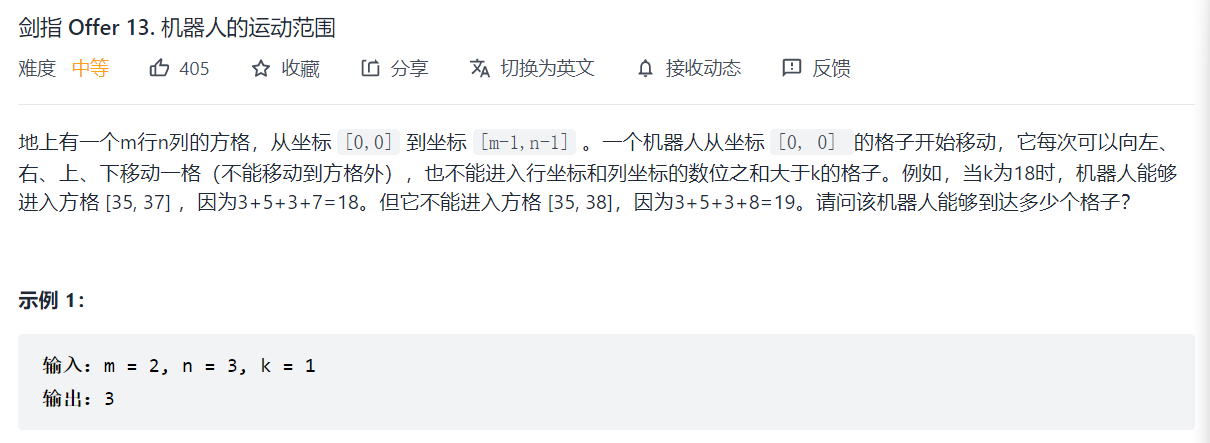
Motion range of the Offer 13 robot
class Solution {
public int movingCount(int m, int n, int k) {
boolean[][] visited = new boolean[m][n];
return dfs(0,0,m,n,k,visited);
}
public int dfs(int i,int j,int m,int n,int k,boolean[][] visited) {
//Hyperboundary
if (i < 0 || i >= m || j < 0 || j >= n) {
return 0;
}
//Over k and visited (prevent turning back)
if (i%10 + i/10 + j/10 + j%10 > k || visited[i][j]) {
return 0;
}
//sign
visited[i][j] = true;
//Spread to surrounding nodes
return 1+dfs(i+1,j,m,n,k,visited)
+dfs(i-1,j,m,n,k,visited)
+dfs(i,j+1,m,n,k,visited)
+dfs(i,j-1,m,n,k,visited);
}
}
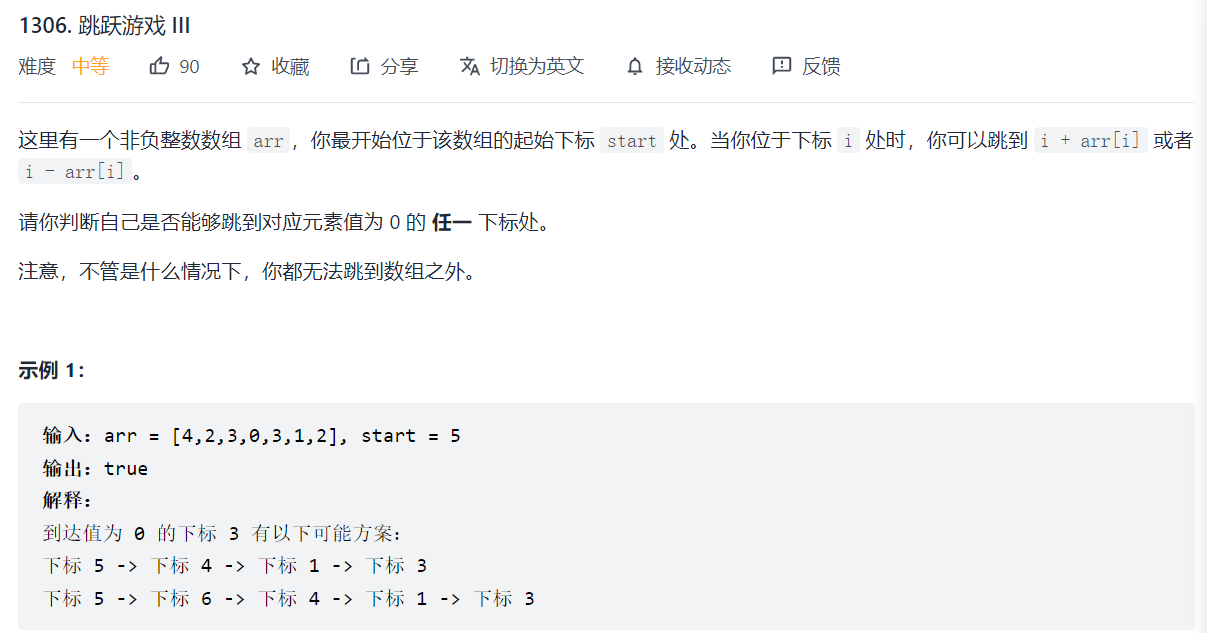
LC 1306 jumping game III
// There are only two types of start + arr [start] start arr [start] for each outward diffusion
class Solution {
public boolean canReach(int[] arr, int start) {
boolean[] visited = new boolean[arr.length];
return dfs(arr,start,visited);
}
public boolean dfs(int[] arr, int start,boolean[] visited) {
//Cross border and visited (avoid going back)
if (start < 0 || start >= arr.length || visited[start]) {
return false;
}
int step = arr[start];
//Mark it
visited[start] = true;
//Successful arrival
if (step == 0) {
return true;
}
return dfs(arr,start+step,visited) || dfs(arr,start - step,visited);
}
}
(3) Binary tree related DFS
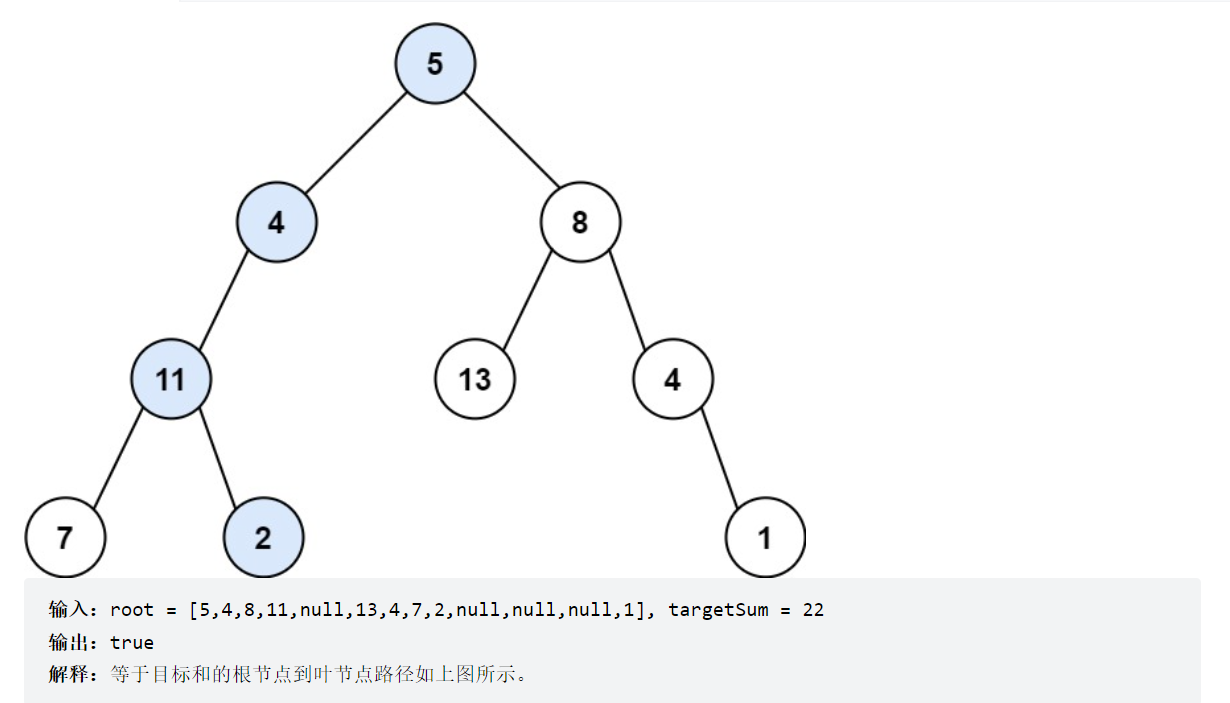
LC112 path sum
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
return dfs(root,targetSum);
}
public boolean dfs (TreeNode root , int targetSum) {
if (root == null) {
return false;
}
if (root.left == null && root.right == null) {
return root.val == targetSum;
}
return dfs(root.left , targetSum - root.val)
|| dfs(root.right , targetSum - root.val);
}
}
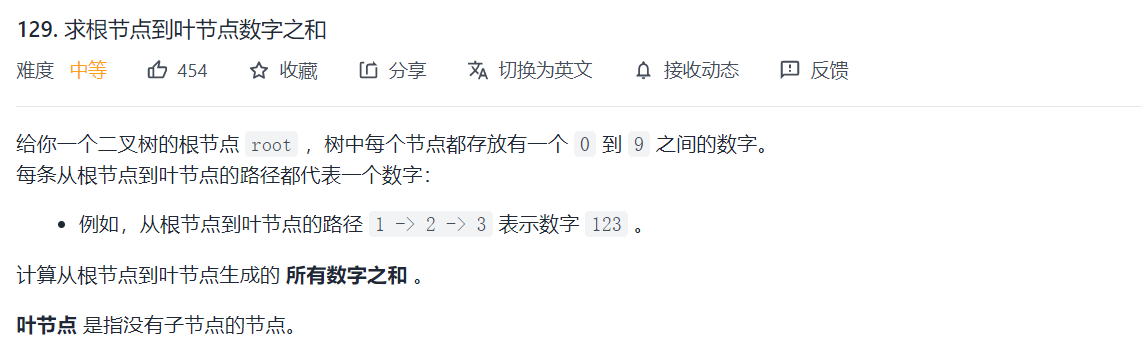
LC129 find the sum of numbers from root node to leaf node
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root , 0);
}
int dfs (TreeNode root , int sum) {
if (root == null)
return 0;
if (root.left == null && root.right == null)
return sum + root.val;
sum += root.val;
return dfs(root.left , 10*sum)
+ dfs(root.right , 10*sum);
}
}