26. Delete new elements in the array

Given a sort array, you need to delete duplicate elements in place so that each element appears only once, returning the new length of the array after removal.

Do not use extra array space, you must modify the input array in place and do so with O(1) extra space.

Example 1:
Given array nums = [1,1,2],
The function should return a new length of 2, and the first two elements of the original array nums are modified to 1, 2.

Example 2:
Given nums = [0,0,1,1,1,2,2,3,3,4],
The function should return a new length of 5, and the first five elements of the original array nums are modified to 0, 1, 2, 3, 4.

class Solution {
    public int removeDuplicates(int[] nums) {
   //i refers to the number to be reserved;
   //j traversing the entire array
   int i = 0;
   for(int j = 1; j < nums.length; j++){
       if(nums[i] != nums[j]){
           i++;//Find the number you need to keep, move i back, make room
           nums[i] = nums[j];
       }
   }
   return i+1;
    }
}

633. Sum of squares

Given a non negative integer c, you need to determine whether there are two integers a and b, so that a2 + b2 = c.

Example 1:
Input: 5
Output: True
Explanation: 1 * 1 + 2 * 2 = 5

Example 2:
Input: 3
Output: False

class Solution {
    public boolean judgeSquareSum(int c) {
     int i = 0;
     int j = (int) Math.sqrt(c);//Square root
     int target = 0;
     //When the sum of squares of two numbers is equal to 2, both i and j are equal to 1, indicating that i can be equal to J
     while(i<=j){
         target = i*i+j*j;
         if(target == c){
             return true;
         }else if(target < c){
             i++;
         }else{
             j--;
         }
     }
     return false;
    }
}

88. Merge two ordered arrays

Given two ordered integer arrays nums1 and nums2, nums2 is merged into nums1, making num1 an ordered array.

Explain:
The number of elements to initialize nums1 and nums2 is m and n, respectively.
You can assume that nums1 has enough space (space size greater than or equal to m + n) to hold the elements in nums2.

Example:
Input:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3

Output: [1,2,2,3,5,6]

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
       //Merge sort
       //Since the fill number is after nums1, it starts traversing from the back to the front
       int i1 = m-1;//Point to the end of nums1
       int i2 = n-1; //Point to the end of nums2
       int index = m+n-1;//Point to the end of the merged array

       while(i1>=0 && i2>= 0){
           //If nums1 is large, fill nums1
           if(nums1[i1] > nums2[i2]){
            nums1[index--] = nums1[i1--];
           }else{
               nums1[index--] = nums2[i2--];
           }
        
       }
       //If there is still an array not filled out;
       //If it's nums1, don't worry, because it's supposed to be filled with nums1;
       //If it's nums2, assign it all
       while(i2>=0){
           nums1[index--] = nums2[i2--];
       }
    }
}

141. Circular list

Given a link list, determine whether there are links in the link list.
In order to represent the links in a given linked list, we use the integer pos to represent the position where the end of the linked list is connected to the linked list (the index starts from 0). If pos is - 1, there are no rings in the list.

Example 1:
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: there is a link in the list with the tail connected to the second node.

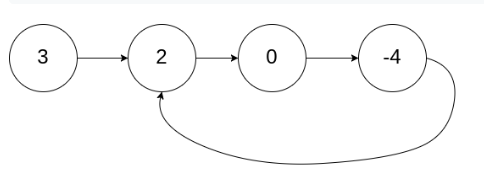
Idea: traverse. If null is encountered, it must not be a ring;
Traversal, if the previous duplicate node is encountered, it must be a ring.
Two solutions: fast and slow pointer; HashMap
Corresponding situation: fast and slow pointer, imagine that two athletes are running long distance on the playground, and will definitely meet at last.
HashMap think of athletes taking photos every few minutes of running. There must be two photos of repeated scenes at last

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        //Head processing
        //Without nodes, a ring cannot be formed;
        //There is only one node, and it can't form a ring
        if(head == null || head.next == null)  return false;

        //Fast and slow pointer
        //Think about running on the playground,
        //If there is a ring, the fast pointer will run twice, and the slow pointer will run once, and they will meet
        ListNode slow = head;
        ListNode fast = head.next;
        while(fast != null && fast.next != null){
           //Now let the fast pointer go two steps
           //Slow pointer one step
           slow = slow.next;
           fast = fast.next.next;
           //If we meet, there is a ring
           if(slow == fast){
               return true;
           }
       }
       return false;      
    }
}

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
 //Thought: judge whether the link list has a ring or not;
 //Find the entrance to the ring
public class Solution {
    public ListNode detectCycle(ListNode head) {
      //First, carry out a self check on the linked list
      if(head == null || head.next == null){
          return null;
      }

      //Define a fast pointer, a slow pointer, and judge whether there is a ring or not
      //Two steps for fast pointer and one step for slow pointer
      //There are a nodes in front of the ring list entry, b nodes in the ring, and a+b nodes in the chain list
      //So when we meet, the fast pointer takes the s+nb step
      //fast is twice the number of slow steps, so f = s+nb = 2s
      //f = 2nb, s= nb, this is the number of steps taken by the two pointers at the first meeting
      //At this time, we want to know that the circular entrance, s has already taken nb steps, so we just need to let s take step a again and stop,
      //After walking through the list, he (s) comes out of the list port, which is the circular entrance
      //You can find out where the ring entrance is
      //We still use the method of double pointer. We define a pointer, start from the beginning, walk with step a of s, and they will meet again at the circular entrance
      //Because they've gone through the chain together
      ListNode fast = head;
      ListNode slow =head;
      boolean hascycle = false;
      while(fast!=null && fast.next != null){
          fast = fast.next.next;
          slow = slow.next;
          if(fast == slow){
              hascycle = true;
              break;
              //break is to jump out of the loop, in this topic, is to jump out of the if statement;
              //Continue is to jump out of this cycle, but the next cycle will continue
          }
      }
      //Define the third pointer. The place where the third pointer and slow pointer meet is the entrance of the ring 
      if(hascycle){
       ListNode third = head;
       while(slow != third){
           slow = slow.next;
           third = third.next;
       }
       return third;
      }
      return null;
}
}