leetcode essence of algorithm interview in Dachang 21. Tree
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
The data structure of tree includes root node, left and right nodes. In the subtree, there are parent nodes, child nodes and brother nodes. Those without child nodes become leaf nodes. The tree is divided into binary tree and multi tree
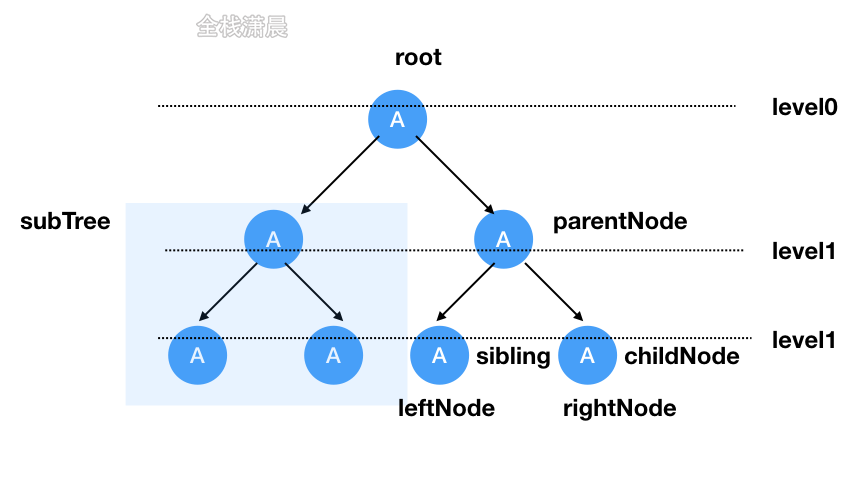
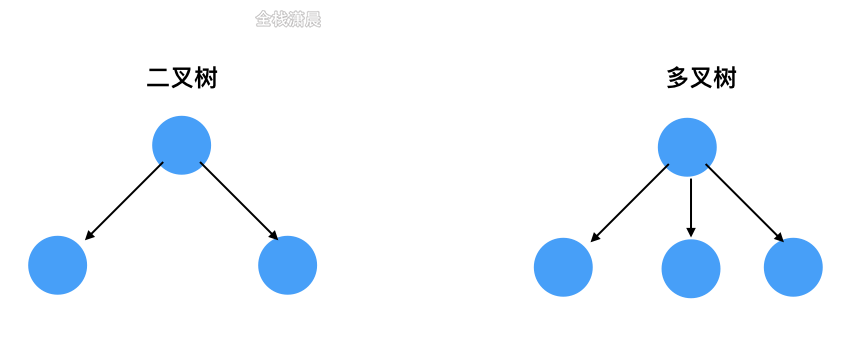
List is a specialized tree, and tree is a specialized Graph
Binary search tree
Binary Search Tree (English: Binary Search Tree), also known as ordered binary tree or sorted binary tree. The following conditions are met:
- If its left subtree is not empty, the values of all nodes on the left subtree are less than its root node.
- If its right subtree is not empty, the values of all nodes on the right subtree are greater than its root node.
- Its left and right subtrees are also binary search trees.
Advantages of binary search tree: it can not only find data, but also insert and delete data efficiently
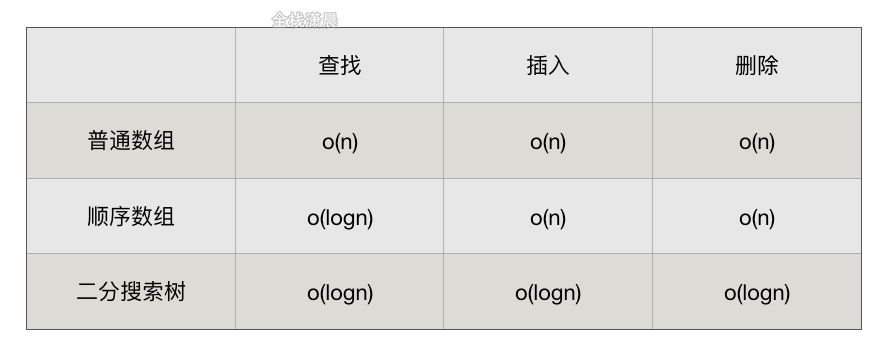
Note that the binary search tree is not necessarily a complete binary tree

Tree traversal
-
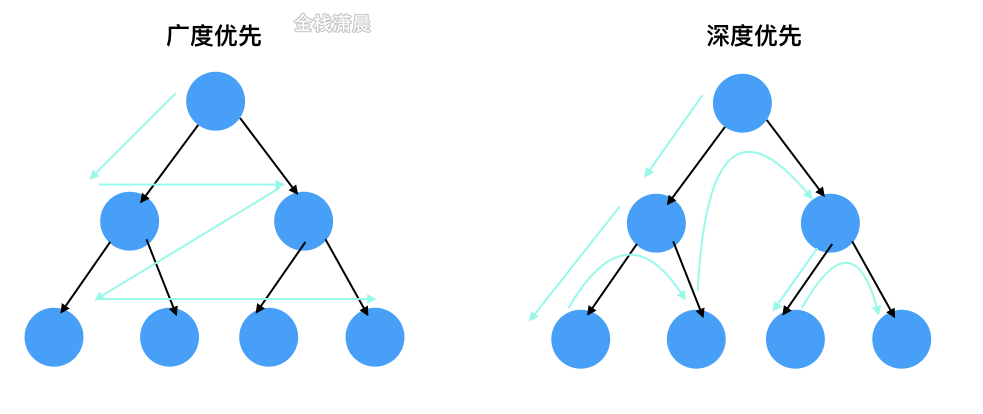
Depth first
-
Breadth first
- Preamble: root left right
- Middle order: left root right
- Post order: left right root
144. Preorder traversal of binary tree(easy)
94. Middle order traversal of binary tree (easy)
145. Post order traversal of binary tree (easy)
The animation is too large. Click to view it
The animation is too large. Click to view it
The animation is too large. Click to view it
The animation is too large. Click to view it
Method 1. Recursion
js:
//Time complexity O(n),n is a tree of nodes, and space complexity O(n), that is, recursive space overhead (tree height). In the worst case, the tree is a linked list, so it is O(n), and the average space complexity O(logn)
//Preorder traversal:
var preorderTraversal = function(root, res = []) {
if (!root) return res;
res.push(root.val);
preorderTraversal(root.left, res)
preorderTraversal(root.right, res)
return res;
};
//Middle order traversal:
var inorderTraversal = function(root, res = []) {
if (!root) return res;
inorderTraversal(root.left, res);
res.push(root.val);
inorderTraversal(root.right, res);
return res;
};
//Post order traversal:
var postorderTraversal = function(root, res = []) {
if (!root) return res;
postorderTraversal(root.left, res);
postorderTraversal(root.right, res);
res.push(root.val);
return res;
};
Java:
//Time complexity O(n),n is a tree of nodes, and space complexity O(n), that is, recursive space overhead (tree height). In the worst case, the tree is a linked list, so it is O(n), and the average space complexity O(logn)
//Preorder traversal
class Solution {
ArrayList<Integer> preOrderReverse(TreeNode root) {
ArrayList<Integer> result = new ArrayList<Integer>();
preOrder(root, result);
return result;
}
void preOrder(TreeNode root, ArrayList<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);
preOrder(root.left, result);
preOrder(root.right, result);
}
}
// Medium order traversal
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list);
list.add(root.val);
inorder(root.right, list);
}
}
// Postorder traversal
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list);
postorder(root.right, list);
list.add(root.val);
}
}
Method 2. Iteration
js:
// The time complexity O(n),n is the node tree, and the space complexity O(n), displays the space overhead of the stack
// Preorder traversal: left and right
// Stack pressing order: right, left, middle
var preorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right); // right
if (node.left) stack.push(node.left); // Left
stack.push(node); // in
stack.push(null);
};
return res;
};
// Middle order traversal: left, middle, right
// Stack pressing order: right, middle and left
var inorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right); // right
stack.push(node); // in
stack.push(null);
if (node.left) stack.push(node.left); // Left
};
return res;
};
// Subsequent traversal: left and right middle
// Stack pressing order: middle right left
var postorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
stack.push(node); // in
stack.push(null);
if (node.right) stack.push(node.right); // right
if (node.left) stack.push(node.left); // Left
};
return res;
};
Java:
// The time complexity O(n),n is the node tree, and the space complexity O(n), displays the space overhead of the stack
// The traversal sequence of the preamble: middle left right, and the stacking sequence: middle right left
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
if (node.right!=null) st.push(node.right);
if (node.left!=null) st.push(node.left);
st.push(node);
st.push(null);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
// Middle order traversal order: left middle right stack order: left right
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
if (node.right!=null) st.push(node.right);
st.push(node);
st.push(null);
if (node.left!=null) st.push(node.left);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
// Post order traversal sequence: left - right - middle stack order: Middle - left - right stack order: Middle - right - left, and finally flip the result
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
st.push(node);
st.push(null);
if (node.right!=null) st.push(node.right);
if (node.left!=null) st.push(node.left);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
98. Validate binary search tree (medium)
Method 1. Recursion

- Idea: using the nature of binary search tree, each node is larger than all nodes in its left subtree and smaller than all nodes in its right subtree, and the left and right subtrees of each node are not empty, then its left and right subtrees are also binary search trees. We can recursively verify the left and right subtrees of each node.
- Complexity analysis: time complexity: O(n), n is a tree of binary tree nodes. Spatial complexity: O(n), n is the number of recursive layers. In the worst case, the binary tree is a chain, and the tree height is n, that is, a total of N layers
Js:
const helper = (root, lower, upper) => {
if (root === null) {
return true;
}
if (root.val <= lower || root.val >= upper) {//The termination condition does not satisfy the properties of binary search tree
return false;
}
//Recursive left and right subtree
return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
}
var isValidBST = function(root) {
//Define low=-Infinity so that all values are greater than low
//Define upper=Infinity so that all values are less than upper
return helper(root, -Infinity, Infinity);
};
Java:
class Solution {
public boolean isValidBST(TreeNode root) {
return helper(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean helper(TreeNode root, long lower, long upper) {
if (root == null) {
return true;
}
if (root.val <= lower || root.val >= upper) {
return false;
}
return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
}
}
Method 2: middle order traversal
The animation is too large. Click to view it
- Idea: from the nature of binary search prime tree, if you traverse the binary search tree in middle order, you will get an ascending array
- Complexity analysis: time complexity: O(n), each element is accessed once. Space complexity: O(n). The medium order traversal uses the stack to store elements, which requires additional O(n) space
Js:
//Non recursive version of middle order traversal
var isValidBST = function(root) {
let stack = [];
let inorder = -Infinity;
while (stack.length || root !== null) {
while (root !== null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (root.val <= inorder) {
return false;
}
inorder = root.val;
root = root.right;
}
return true;
};
//Recursive version of middle order traversal
var isValidBST = function (root) {
let arr = [];
const buildArr = (root) => {
if (root) {
buildArr(root.left);
arr.push(root.val);
buildArr(root.right);
}
}
buildArr(root);
for (let i = 1; i < arr.length; ++i) {
if (arr[i] <= arr[i - 1])
return false;
}
return true;
};
Java:
class Solution {
public boolean isValidBST(TreeNode root) {
Deque<TreeNode> stack = new LinkedList<TreeNode>();
double inorder = -Double.MAX_VALUE;
while (!stack.isEmpty() || root != null) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (root.val <= inorder) {
return false;
}
inorder = root.val;
root = root.right;
}
return true;
}
}
236. Nearest common ancestor of binary tree (medium)
Method 1. Recursion
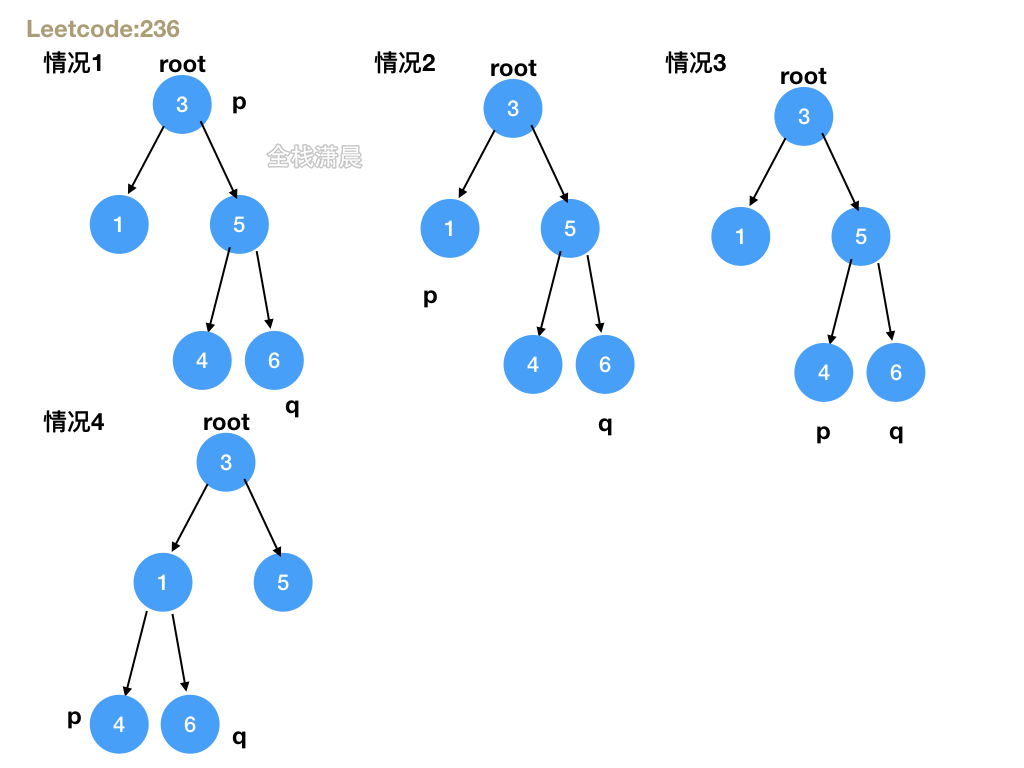
- Idea: there are four situations: 1.root is null or root is equal to p or q, indicating that root is the common ancestor of p and q. 2. Recurse the left and right subtrees. If the left and right subtree recursive functions do not return null, root is the common ancestor of p and q. 3. If the left subtree recursive function returns null, p and q are in the right subtree. 4. If the right subtree recursive function returns null, p, q is in the left subtree
- Complexity analysis: time complexity: O(n), n is a tree of binary tree nodes, space complexity: O(n), n is a recursive layer
Js:
var lowestCommonAncestor = function(root, p, q) {
// 1. Determine recursive functions
const travelTree = function(root,p,q) {
// 2. Determine recursive termination conditions
if(root === null || root === p||root === q) {
return root;
}
// 3. Determine recursive single layer logic
let left = travelTree(root.left,p,q);
let right = travelTree(root.right,p,q);
//If p and q can be found in both the left and right subtrees of a node, it means that the node is a common ancestor
if(left !== null&&right !== null) {
return root;
}
if(left ===null) {//If the left subtree is not found, it means that p and q are all in the right subtree
return right;
}
return left;//If the right subtree is not found, it means that p and q are all in the left subtree
}
return travelTree(root,p,q);//Recursive start
};
Java:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return travelTree(root, p, q);
}
public TreeNode travelTree(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) {
return root;
}
TreeNode left = travelTree(root.left, p, q);
TreeNode right = travelTree(root.right, p, q);
if (left != null && right != null) {// The left and right subtrees are found respectively, indicating that the root at this time is the required result
return root;
}
if (left == null) {
return right;
}
return left;
}
}
235. Nearest common ancestor of binary search tree (easy)
**Method 1: * * find the path of p or q from the left and right subtrees of the binary search tree, and finally find the first same node of the two paths, time complexity O(n), space complexity O(n)
Method 2: recursion
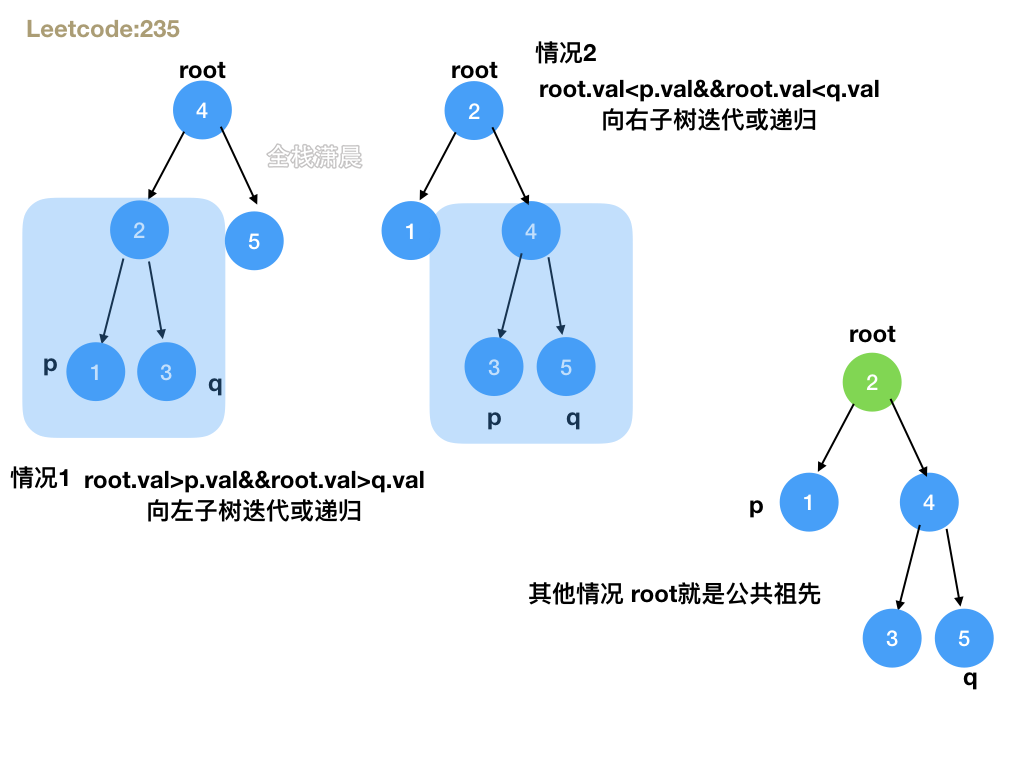
- Idea: there are three cases: 1. The root node is greater than p and greater than q, indicating that both p and q are in the left subtree of root; 2. The root node is less than p and less than q, indicating that both p and q are in the right subtree of root; 3. Other cases, such as root is equal to p or q, indicating that root is the common ancestor. In the first two cases, it directly recurses the left and right subtrees, and in the third case, it directly returns root
- Complexity analysis: time complexity: O(n). N is a tree of binary tree nodes. Space complexity: O(n). N is the number of recursive layers. In the worst case, it is equal to N. at this time, the tree is a linked list
Js:
var lowestCommonAncestor = function(root, p, q) {
if(root === null) {//Recursive termination condition
return root;
}
//If the root node is greater than p and greater than q, both p and q are in the left subtree of root
if(root.val>p.val&&root.val>q.val) {
let left = lowestCommonAncestor(root.left,p,q);
return left !== null&&left;
}
//If the root node is less than p and less than q, both p and q are in the right subtree of root
if(root.val<p.val&&root.val<q.val) {
let right = lowestCommonAncestor(root.right,p,q);
return right !== null&&right;
}
return root;//If none of the above conditions are met, root is a common ancestor
};
Java:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
return root;
}
}
Method 3: iteration
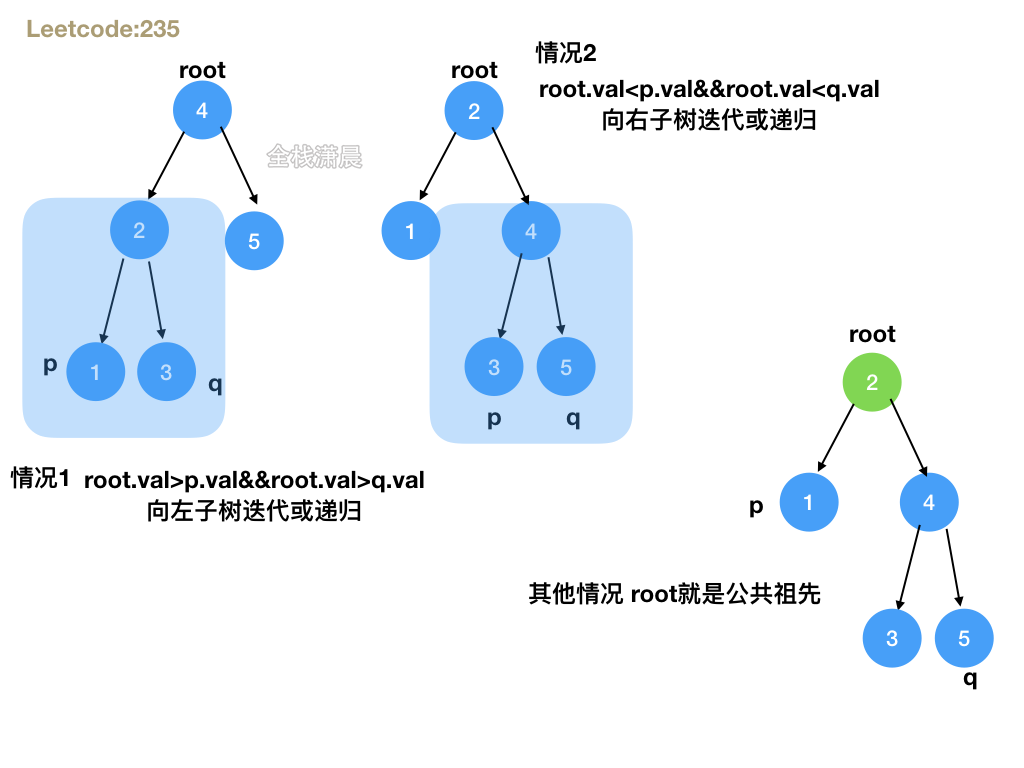
- Idea: it's the same as recursion, except that the root variable is used to iterate over the left and right subtrees
- Complexity analysis: time complexity: O(n), space complexity: O(1), n is a tree of binary tree nodes
js:
var lowestCommonAncestor = function(root, p, q) {
while(root) {
if(root.val>p.val&&root.val>q.val) {
root = root.left;
}else if(root.val<p.val&&root.val<q.val) {
root = root.right;
}else {
return root;
}
}
return null;
};
java:
//java
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while (true) {
if (root.val > p.val && root.val > q.val) {
root = root.left;
} else if (root.val < p.val && root.val < q.val) {
root = root.right;
} else {
break;
}
}
return root;
}
}
102. Sequence traversal of binary tree (medium)
Method 1. Breadth first traversal
The animation is too large. Click to view it
- Idea: prepare a queue, add the root node to the queue, cycle the queue when the queue is not empty, get the size of the current queue each cycle, cycle each element of the current layer, and then add it to the output array ret. if there are left and right nodes in this element, add the left and right nodes to the queue
- Complexity analysis: the time complexity is O(n), and each point enters and exits the team once, so the progressive time complexity is O(n). The space complexity is O(n), and the number of elements in the queue does not exceed n
Js:
var levelOrder = function(root) {
const ret = [];
if (!root) {
return ret;
}
const q = [];
q.push(root);//Initial queue
while (q.length !== 0) {
const currentLevelSize = q.length;//Number of nodes in the current layer
ret.push([]);//New layer push array
for (let i = 1; i <= currentLevelSize; ++i) {//Loops the nodes of the current layer
const node = q.shift();
ret[ret.length - 1].push(node.val);//Push array of current layer
if (node.left) q.push(node.left);//Check the left node. If there is a left node, continue to join the queue
if (node.right) q.push(node.right);//Check the left and right nodes. If there is a right node, continue to join the queue
}
}
return ret;
};
Java:
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<List<Integer>>();
if (root == null) {
return ret;
}
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.offer(root);
while (!q.isEmpty()) {
List<Integer> level = new ArrayList<Integer>();
int currentLevelSize = q.size();
for (int i = 1; i <= currentLevelSize; ++i) {
TreeNode node = q.poll();
level.add(node.val);
if (node.left != null) {
q.offer(node.left);
}
if (node.right != null) {
q.offer(node.right);
}
}
ret.add(level);
}
return ret;
}
}
Method 2: depth first traversal
The animation is too large. Click to view it
- Idea: start from the root node, recurse the left and right subtrees continuously, and pass through the step layers and res output array.
- Complexity analysis: time complexity O(n),n is the number of nodes. Spatial complexity O(n),n is the height of the tree.
js:
var levelOrder = function(root) {
if(!root) return []
let res = []
dfs(root, 0, res)
return res
};
function dfs(root, step, res){//Each layer transparently transmits the current node, number of layers, and output array
if(root){
if(!res[step]) res[step] = []//Initializes the current layer array
res[step].push(root.val)//Add the current node to the current layer array
dfs(root.left, step + 1, res)//step+1, recursive left node
dfs(root.right, step + 1, res)//step+1, recursive right node
}
}
Java:
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if(root != null){
dfs(res, root, 0);
}
return res;
}
private void dfs(List<List<Integer>> res, TreeNode node, int step){
if(res.size() - 1 < step){
res.add(new ArrayList<Integer>());
}
res.get(step).add(node.val);
if(node.left!=null){
dfs(res, node.left, step + 1);
}
if(node.right!=null){
dfs(res, node.right, step + 1);
}
}
}
107. Sequence traversal of binary tree II (medium)
Time complexity O(n), space complexity O(n)
js:
const levelOrderBottom = (root) => {
if (root == null) {
return [];
}
const queue = [];
queue.push(root);
const res = [];
while (queue.length) {
const subRes = [];
const levelSize = queue.length;
for (let i = 0; i < levelSize; i++) {
const cur = queue.shift();
subRes.push(cur.val);
if (cur.left) {
queue.push(cur.left);
}
if (cur.right) {
queue.push(cur.right);
}
}
res.unshift(subRes);//Different from 102, the direction of pushing into res is exactly the opposite
}
return res;
}
java:
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> res = new LinkedList<List<Integer>>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> subRes = new ArrayList<Integer>();
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode cur = queue.poll();
subRes.add(cur.val);
TreeNode left = cur.left, right = cur.right;
if (left != null) {
queue.offer(left);
}
if (right != null) {
queue.offer(right);
}
}
res.add(0, subRes);
}
return res;
}
}
104. Maximum depth of binary tree (easy)
Method 1.dfs
The animation is too large. Click to view it
- Idea: the depth of a node is equal to 1 plus the greater of the left node and the node depth. The formula is h(r)=Math.max(h(r.left), h(right)) + 1, so you can traverse the left and right subtrees in depth and return the maximum depth of the left and right subtrees.
- Complexity analysis: time complexity O(n), where n is the number of binary tree nodes. Spatial complexity O(n), where n represents the height of the binary tree. In the worst case, it is the same as the number of nodes of the tree
js:
var maxDepth = function(root) {
if(!root) {
return 0;
} else {
const left = maxDepth(root.left);//Recursive left subtree
const right = maxDepth(root.right);//Recursive right subtree
return Math.max(left, right) + 1;//1 plus the greater of the left node and the node depth
}
};
Java:
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) {
return 0;
} else {
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return Math.max(left, right) + 1;
}
}
}
Method 2.bfs
The animation is too large. Click to view it
- Idea: the sequence traverses the binary tree, and at the end of each layer, depth is added by 1
- Complexity analysis: time complexity O(n), n is the number of nodes of the binary tree, and each node will be accessed only once. The spatial complexity O(n) represents the number of elements stored in the queue. In the worst case, it is the same as the number of binary tree nodes
Js:
const maxDepth = (root) => {
if (root == null) return 0;
const queue = [root];
let depth = 1;
while (queue.length) {
// Number of nodes in the current layer
const levelSize = queue.length;
// List the nodes of the current layer one by one
for (let i = 0; i < levelSize; i++) {
// Currently dequeued node
const cur = queue.shift();
// The left and right child nodes are listed
if (cur.left) queue.push(cur.left);
if (cur.right) queue.push(cur.right);
}
// All nodes in the current layer have been listed. If the queue is not empty, it indicates that there are nodes in the next layer, depth+1
if (queue.length) depth++;
}
return depth;
};
Java:
class Solution {
public int maxDepth(TreeNode root) {
if(root == null){
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
while(!queue.isEmpty()){
int levelSize = queue.size();
for(int i = 0; i < levelSize; i++){
TreeNode node = queue.poll();
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
depth++;
}
return depth;
}
}
111. Minimum depth of binary tree (easy)
Method 1.dfs
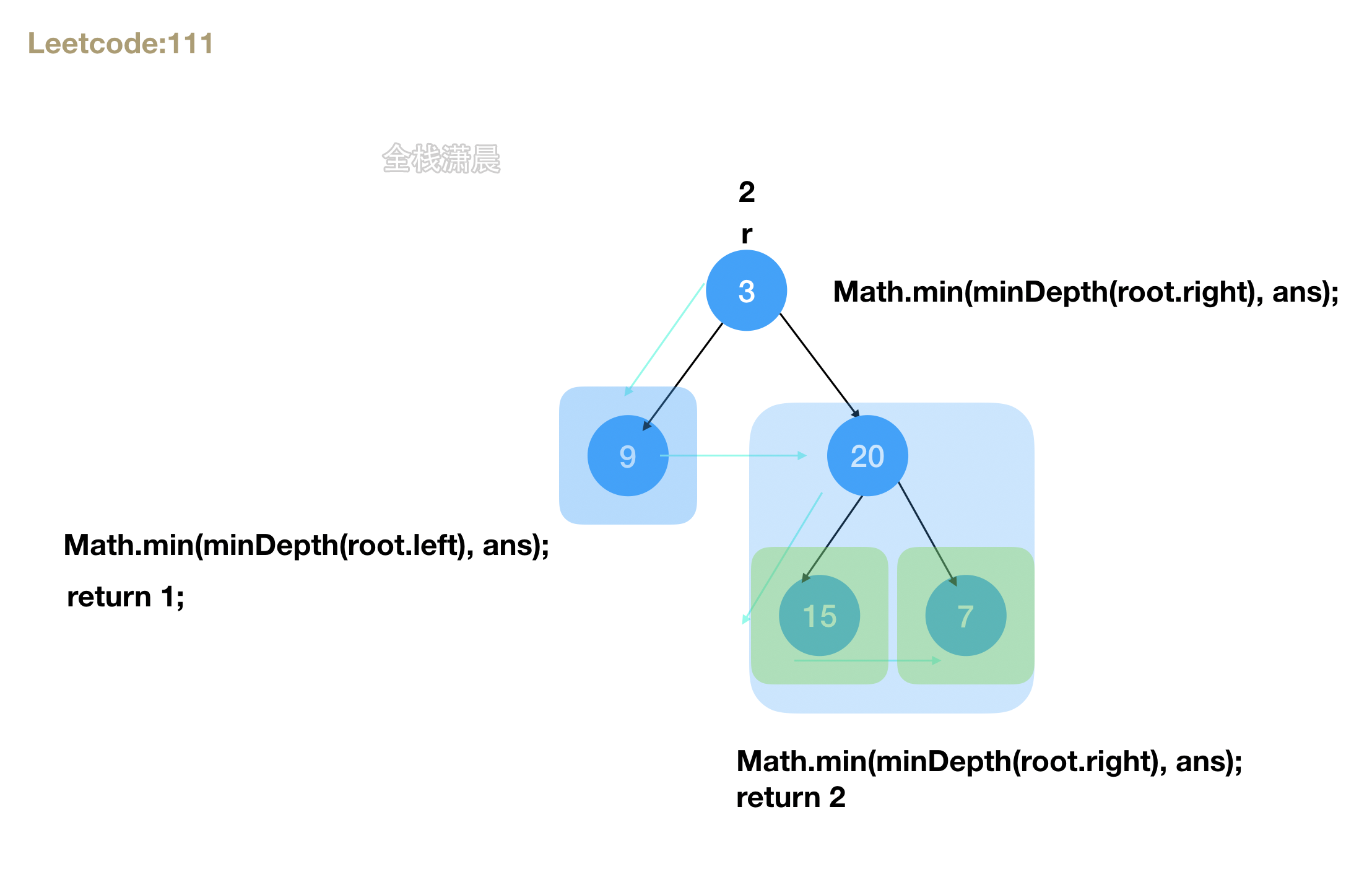
- Idea: depth first traverses the left and right subtrees and decomposes them into sub problems. The minimum depth of the tree is equal to the minimum depth of the left and right subtrees + 1
- Complexity analysis: time complexity O(n), where n is the number of binary tree nodes. Spatial complexity O(n), where n represents the height of the binary tree. In the worst case, the tree is chain like and has the same number of nodes as the tree. On average, the height of the tree is positively correlated with the logarithm of the number of nodes, and the spatial complexity is O(logn)
js:
var minDepth = function(root) {
if(root == null) {
return 0;
}
if(root.left == null && root.right == null) {//Traverse to leaf node termination
return 1;
}
let ans = Number.MAX_SAFE_INTEGER;
if(root.left != null) {
ans = Math.min(minDepth(root.left), ans);//Recurse the left subtree to find the minimum depth of the left subtree
}
if(root.right != null) {
ans = Math.min(minDepth(root.right), ans);//Recursive right subtree to find the minimum depth of right subtree
}
return ans + 1;//The minimum depth is equal to the minimum depth of left and right subtrees + 1
};
Java:
class Solution {
public int minDepth(TreeNode root) {
if(root == null) {
return 0;
}
if(root.left == null && root.right == null) {
return 1;
}
int ans = Integer.MAX_VALUE;
if(root.left != null) {
ans = Math.min(minDepth(root.left), ans);
}
if(root.right != null) {
ans = Math.min(minDepth(root.right), ans);
}
return ans + 1;
}
}
Method 2.bfs
The animation is too large. Click to view it
- Idea: breadth first traverses the binary tree. The depth of each layer is + 1. When the first leaf node terminates, the depth at this time is the minimum depth
- Complexity analysis: time complexity O(n), n is the number of nodes of the binary tree, and each node will be accessed only once. The spatial complexity O(n) represents the number of elements stored in the queue. In the worst case, it is the same as the number of binary tree nodes
js:
var minDepth = function(root) {
if(root == null) return 0;
let q = [root];
//root itself is a layer, so the depth is initialized to 1
let depth = 1;
while(q.length){
let len = q.length;
for(let i=0; i<len; i++){
let curr = q.shift();
//Determine whether the current node is a leaf node
if(curr.left == null && curr.right == null){
return depth;
}
//If it is not a leaf node, its adjacent nodes are added to the queue
if(curr.left){
q.push(curr.left);
}
if(curr.right){
q.push(curr.right);
}
}
depth++;
}
return depth;
};
Java:
class Solution {
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
int depth = 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
int sz = q.size();
depth++;
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
if (cur.left == null && cur.right == null) {
return depth;
}
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
return depth;
}
}
127. Word Solitaire (hard)
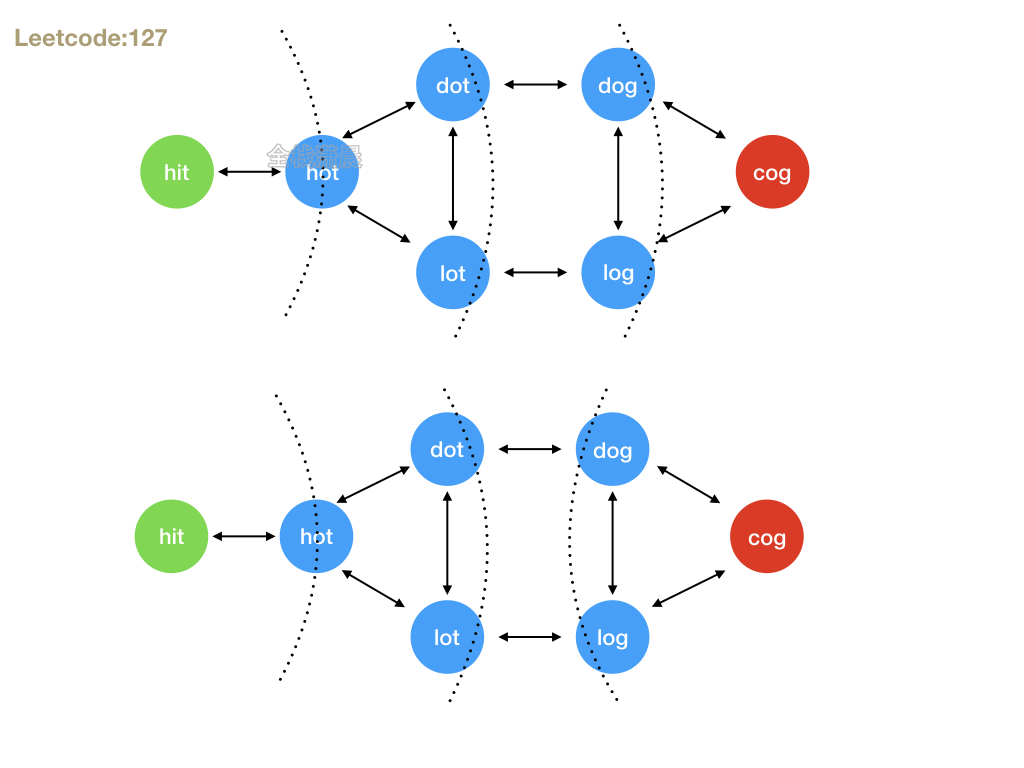
- Idea: bfs, loop beginWord, replace 26 lowercase characters for each character, and see whether the newly generated word is in the wordList. If it exists, it is a legal path. Until the newly generated word is endWord, the loop returns 0 when it is completed or does not reach endWord. The idea of two-way bfs is the same, but it is to move closer from both sides to the middle to judge whether the newly generated word is in the path in the other direction.
Method 1:bfs
js:
const ladderLength = (beginWord, endWord, wordList) => {
const wordSet = new Set(wordList);
const queue = [];
queue.push([beginWord, 1]);//Start adding words and levels to the queue
while (queue.length) {
const [word, level] = queue.shift()//Team out for bfs
if (word == endWord) {//Return level equal to endword
return level;
}
for (let i = 0; i < word.length; i++) { //Circular word list
for (let c = 97; c <= 122; c++) { //Loop 26 lowercase characters
//Get new words
const newWord = word.slice(0, i) + String.fromCharCode(c) + word.slice(i + 1);
if (wordSet.has(newWord)) { //Check that the wordset package does not include the newly generated words to avoid repetition
queue.push([newWord, level + 1]); //Add new words to the queue
wordSet.delete(newWord); //Avoid dead cycle
}
}
}
}
return 0; // bfs ends and never meets the end
};
Method 2: bidirectional bfs
js:
var ladderLength = function(beginWord, endWord, wordList) {
let wordSet = new Set(wordList)
if (!wordSet.has(endWord)) return 0
//From beginWord to endWord
let begSet = []
//From endWord to beginWord
let endSet = []
begSet.push(beginWord)
endSet.push(endWord)
let n = 1//Hierarchy
while(begSet.length > 0){//Start traversing words
const nextBegins = []//bfs next level word array
//Change a few steps to make the slow one take a few steps
if(begSet.length > endSet.length){
let q = begSet
begSet = endSet
endSet = q
}
//Loop begSet
for(let k = 0; k < begSet.length;k++){
let m = begSet[k]
for(let i = 0; i < m.length; i++){
for (let c = 97; c <= 122; c++){
//Generate new words
let newm = m.slice(0, i) + String.fromCharCode(c) + m.slice(i + 1);
if(endSet.includes(newm)){//meet
return n + 1
}
if( wordSet.has(newm)){
nextBegins.push(newm) //Word array of bfs in the next layer
wordSet.delete(newm) //Prevent duplication
}
}
}
}
begSet = nextBegins
n++ //Level + 1
}
return 0
};
297. Serialization and deserialization of binary tree (hard)
Method 1. Recursive dfs
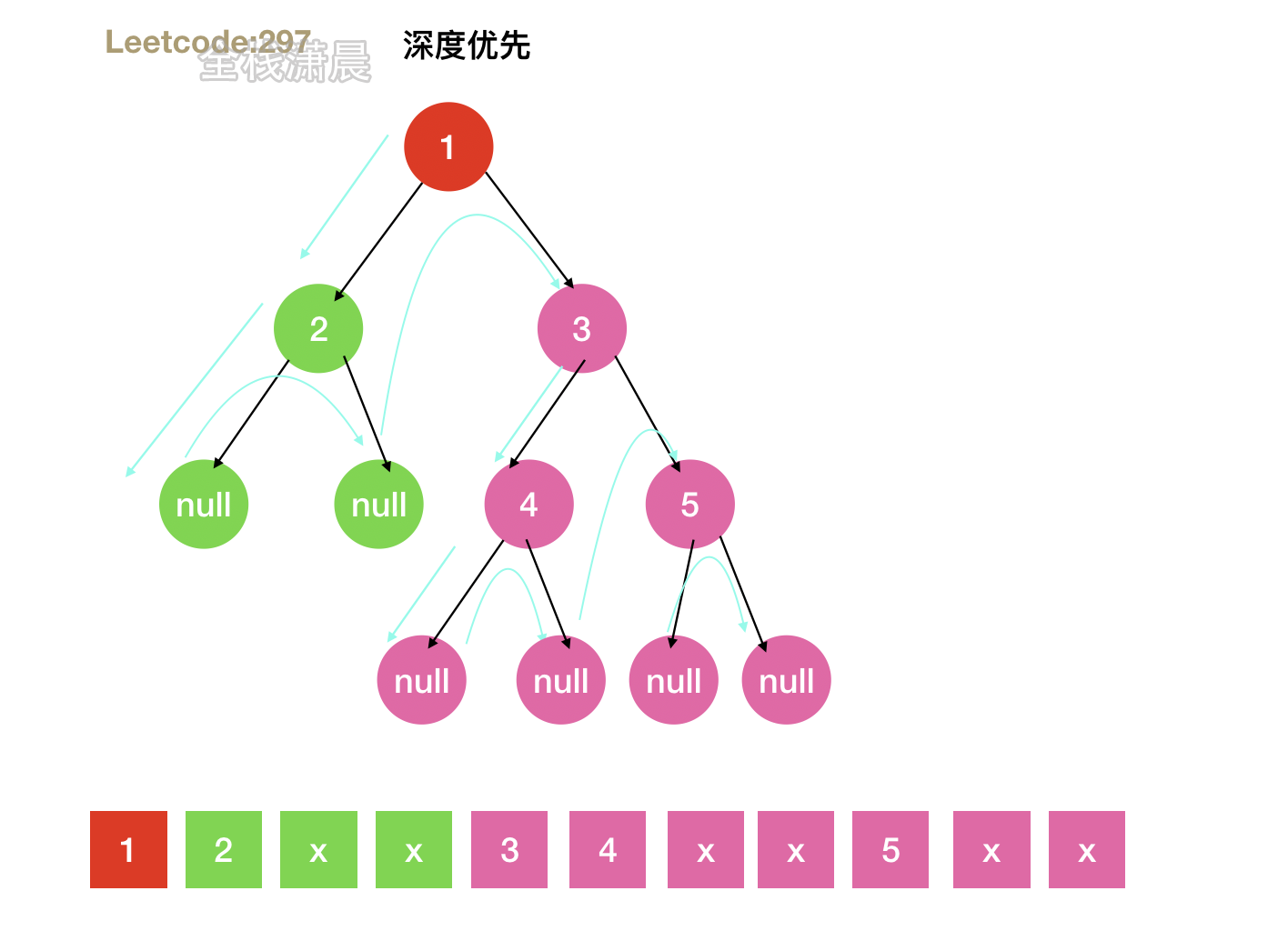
- Idea: depth first traversal, return strings by root, left and right, facilitate the construction from the root node during deserialization, and recurse the left and right subtrees until a null node is encountered.
- Complexity: time complexity O(n). Each node is accessed once. N is the number of nodes in the tree. The space complexity is O(n). In the worst case, the recursion depth is n
js:
const serialize = (root) => {
if (root == null) { //If null is encountered, return 'X' for marking
return 'X';
}
const left = serialize(root.left); //Serialize left subtree
const right = serialize(root.right); //Serialized right subtree
return root.val + ',' + left + ',' + right; //Return string by root, left and right
};
const deserialize = (data) => {
const list = data.split(','); //String to array
const buildTree = (list) => { //Build tree
const rootVal = list.shift(); //First element
if (rootVal == "X") { //null if X
return null;
}
const root = new TreeNode(rootVal); //If it is not X, create a node
root.left = buildTree(list); //Build left subtree
root.right = buildTree(list); //Constructing right subtree
return root; //Returns the built node
};
return buildTree(list);
};
Method 2:bfs
The animation is too large. Click to view it
- Idea: breadth first traverse the nodes, keep the child nodes in the queue, and serialize and deserialize according to the order around the root
- Complexity: time complexity O(n). Each node is accessed once. N is the number of nodes in the tree. Space complexity O(n), space of queue
js:
const serialize = (root) => {
const queue = [root];
let res = [];
while (queue.length) {
const node = queue.shift(); //Out of the team
if (node) { //node exists around the root
res.push(node.val);
queue.push(node.left);
queue.push(node.right);
} else { //If 'x' is not present
res.push('X');
}
}
return res.join(','); //Convert array to string
}
const deserialize = (data) => {
if (data == 'X') return null;
const list = data.split(','); //String to array
const root = new TreeNode(list[0]); //Build from team leader
const queue = [root]; //The root node joins the queue
let cursor = 1; //How many nodes have you traversed
while (cursor < list.length) { //When the queue is not traversed
const node = queue.shift(); //Out of the team
const leftVal = list[cursor]; //Left node value
const rightVal = list[cursor + 1]; //Value of the right node
if (leftVal != 'X') { //Is not an empty node
const leftNode = new TreeNode(leftVal); //Build left node
node.left = leftNode; //The left node is hung under the left of the parent node
queue.push(leftNode); //List yourself and build a subtree with your own root
}
if (rightVal != 'X') {
const rightNode = new TreeNode(rightVal);
node.right = rightNode;
queue.push(rightNode);
}
cursor += 2; //Number of nodes built + 2
}
return root; //Return root
};
226. Flip binary tree (easy)
Method 1: recursion
- Idea: recurse the left and right subtrees and reverse the left and right nodes
- Complexity: the time complexity is O(n), and each node of the tree will be traversed. Space complexity O(n), recursive stack space, in the worst case, is the same as the number of nodes n
js:
var invertTree = function(root) {
if (root === null) {//Recursive termination condition
return null;
}
const left = invertTree(root.left);//Recursive left subtree
const right = invertTree(root.right);//Recursive right subtree
//Swap left and right nodes
root.left = right;
root.right = left;
return root;
};
java:
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode left = invertTree(root.left);
TreeNode right = invertTree(root.right);
root.left = right;
root.right = left;
return root;
}
}
100. Same tree(easy)
Method 1.dfs recursion
- Idea: recursively compare left and right subtrees
- Complexity: time complexity O(n). N is the number of nodes in a tree with fewer nodes. If one node is null and the other is not null, the recursion will stop. Space complexity O(n). The recursion depth will not exceed the number of nodes
js:
var isSameTree = function(p, q) {
if(p == null && q == null) //null means the same
return true;
if(p == null || q == null) //Only one is null, which means different
return false;
if(p.val != q.val) //Nodes have different values
return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);//Recursive left and right subtree
};
java:
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p == null && q == null)
return true;
if(p == null || q == null)
return false;
if(p.val != q.val)
return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
Method 2bfs:
- Complexity: time complexity O(n), n is the number of nodes in the tree with fewer nodes, space complexity O(n), and the space of the queue will not exceed the number of nodes in the tree with fewer nodes
js:
var isSameTree = function(p, q) {
let pQ = [p], qQ = [q], res = true
while (pQ.length) {
pNode = pQ.shift()
qNode = qQ.shift()
if (pNode === null && qNode === null) {
res = true
} else if (pNode === null || qNode === null) {
res = false
break
} else {
if (pNode.val !== qNode.val) {
res = false
break
} else {
pQ.push(pNode.left)
pQ.push(pNode.right)
qQ.push(qNode.left)
qQ.push(qNode.right)
}
}
}
return res
};
java:
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
Queue<TreeNode> pQ = new LinkedList<TreeNode>();
Queue<TreeNode> qQ = new LinkedList<TreeNode>();
pQ.offer(p);
qQ.offer(q);
boolean res = true;
while (!pQ.isEmpty()) {
TreeNode pNode = pQ.poll();
TreeNode qNode = qQ.poll();
if (pNode == null && qNode == null) {
res = true;
} else if (pNode == null || qNode == null) {
res = false;
break ;
} else {
if (pNode.val != qNode.val) {
res = false;
break ;
} else {
pQ.offer(pNode.left);
pQ.offer(pNode.right);
qQ.offer(qNode.left);
qQ.offer(qNode.right);
}
}
}
return res;
}
}
101. Symmetric binary tree (easy)
Method 1.dfs recursion
- Complexity: time complexity O(n), traversal of each node once, space complexity O(n), recursive stack depth, the deepest not exceeding n
js:
var isSymmetric = function(root) {
if(!root) return true
const isMirror = (l, r) => {
if(!l && !r) return true; //Two empty nodes are also mirrored
if(
l && r && l.val === r.val && //If the left node and the right node are the same, and the left subtree and the right subtree are also symmetrical, true is returned
isMirror(l.left, r.right) &&
isMirror(l.right, r.left)
) {
return true;
}
return false;
}
return isMirror(root.left, root.right)
};
java:
class Solution {
public boolean isSymmetric(TreeNode root) {
return isMirror(root, root);
}
public boolean isMirror(TreeNode l, TreeNode r) {
if (l == null && r == null) {
return true;
}
if (l == null || r == null) {
return false;
}
return l.val == r.val && isMirror(l.left, r.right) && isMirror(l.right, r.left);
}
}
Method 2.bfs
- Complexity: time complexity O(n), traversal of each node, space complexity O(n), space of the queue
js:
function isSymmetric(root) {
const isMirror = (l, r) => {
const queue = [l, r];
while (queue.length) {
const u = queue.shift();
const v = queue.shift();
if (!u && !v) continue; //Two empty nodes are also mirrored
//Only one of the left and right nodes is empty, or the values are different. false is returned
if (!u || !v || u.val !== v.val) return false;
queue.push(u.left, v.right); //Join the left subtree of the left node and the right subtree of the right node
queue.push(v.left, u.right); //Join the left subtree of the right node and the right subtree of the left node
}
return true;
};
return isMirror(root.left, root.right);
}
java:
class Solution {
public boolean isSymmetric(TreeNode root) {
return isMirror(root, root);
}
public boolean isMirror(TreeNode u, TreeNode v) {
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(u);
queue.offer(v);
while (!queue.isEmpty()) {
u = queue.poll();
v = queue.poll();
if (u == null && v == null) {
continue;
}
if ((u == null || v == null) || (u.val != v.val)) {
return false;
}
queue.offer(u.left);
queue.offer(v.right);
queue.offer(u.right);
queue.offer(v.left);
}
return true;
}
}
112. Path sum (easy)
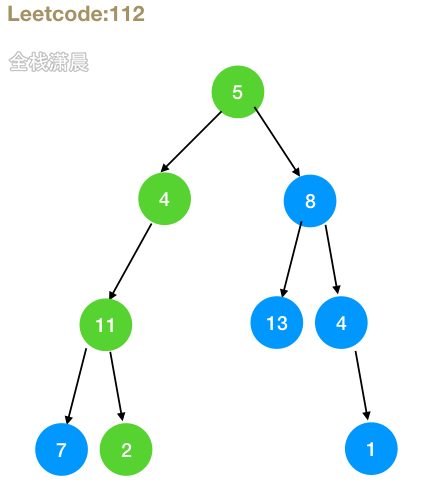
- Idea: recurse the left and right subtrees and constantly let sum subtract the value of the current node. If one of the left and right subtrees returns true, such a path is found
- Complexity: time complexity O(n), n is the number of nodes, and each node is traversed once. The space complexity O(n), which depends on the recursive stack space, is O(n) in the worst case
js:
const hasPathSum = (root, sum) => {
if (root == null) {//Recursive termination condition
return false;
}
if (root.left == null && root.right == null) {//Traverse to leaf node
return sum - root.val == 0; //sum is exactly reduced to 0, return true, otherwise return false
}
//Recursive left and right subtrees, one of which returns true to find such a path
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}
java:
class Solution {
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) {
return false;
}
if (root.left == null && root.right == null) {
return sum == root.val;
}
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}
}
437. Path sum III (medium)
Method 1:dfs
- Idea: recurse the left and right subtrees. In the recursive sub stage, continue to find the path with this node as the root node
- Complexity: the time complexity is O(n^2). All nodes must traverse one side and find out whether there are qualified paths in the subtree with this node as the root. Space complexity O(n), recursive space
js:
var pathSum = function(root, targetSum) {
if (root == null) {
return 0;
}
let ret = rootSum(root, targetSum);//Find the path in the tree with root as the root node
ret += pathSum(root.left, targetSum);//Recursive left subtree to find the path in the left subtree
ret += pathSum(root.right, targetSum);//Recursive right subtree to find the path in the left subtree
return ret;
};
const rootSum = (root, targetSum) => {
let ret = 0;
if (root == null) {
return 0;
}
const val = root.val;
if (val === targetSum) {
ret++;
}
//Take root.left as the root node and targetSum - val as the search path and continue to search for the path
ret += rootSum(root.left, targetSum - val);
//Take root.right as the root node and targetSum - val as the search path and continue to search for the path
ret += rootSum(root.right, targetSum - val);
return ret;
}
java:
class Solution {
public int pathSum(TreeNode root, int targetSum) {
if (root == null) {
return 0;
}
int ret = rootSum(root, targetSum);
ret += pathSum(root.left, targetSum);
ret += pathSum(root.right, targetSum);
return ret;
}
public int rootSum(TreeNode root, int targetSum) {
int ret = 0;
if (root == null) {
return 0;
}
int val = root.val;
if (val == targetSum) {
ret++;
}
ret += rootSum(root.left, targetSum - val);
ret += rootSum(root.right, targetSum - val);
return ret;
}
}
Method 2: prefix and

- Idea: record the path and curr from the root node to the node. Recurse the left and right subtrees to see if there is a path with curr - targetSum as the path sum in the previously traversed path. If so, subtracting this path from the path from the root node to the current node is one of the qualified paths. See the figure
- Complexity: the time complexity is O(n), and the nodes in the binary tree are traversed only once. Space complexity O(n), recursive stack depth.
js:
var pathSum = function(root, targetSum) {
const prefix = new Map();//Store prefix and its number of paths
prefix.set(0, 1);//The number of initialization prefixes and is 0
return dfs(root, prefix, 0, targetSum);
}
const dfs = (root, prefix, curr, targetSum) => {//curr refers to the sum on the path to the current node
if (root == null) {//An empty node has no path and returns 0
return 0;
}
let ret = 0;
curr += root.val;//Add current node
ret = prefix.get(curr - targetSum) || 0;//Gets the number of prefixes and with curr - targetSum
prefix.set(curr, (prefix.get(curr) || 0) + 1);//Add the prefix and number of curl in prefix
ret += dfs(root.left, prefix, curr, targetSum);//Recursive left subtree plus left subtree prefix and the number of paths for targetSum
ret += dfs(root.right, prefix, curr, targetSum);//Recursive right subtree plus right subtree prefix and the number of paths for targetSum
prefix.set(curr, (prefix.get(curr) || 0) - 1);//After node recursion, backtrack the prefix and quantity of curr to avoid double calculation
return ret;
}
java:
class Solution {
public int pathSum(TreeNode root, int targetSum) {
HashMap<Long, Integer> prefix = new HashMap<>();
prefix.put(0L, 1);
return dfs(root, prefix, 0, targetSum);
}
public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {
if (root == null) {
return 0;
}
int ret = 0;
curr += root.val;
ret = prefix.getOrDefault(curr - targetSum, 0);
prefix.put(curr, prefix.getOrDefault(curr, 0) + 1);
ret += dfs(root.left, prefix, curr, targetSum);
ret += dfs(root.right, prefix, curr, targetSum);
prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);
return ret;
}
}
257. All paths of binary tree (easy)
Method 1:dfs
- Idea: recurse the left and right subtrees until the leaf node. In the process of recursion, the path is continuously transmitted. Each layer of recursion is connected to the value of the current node
- Complexity: the time complexity is O(n), and each node is traversed once. Space complexity O(n), recursive stack space
js:
var binaryTreePaths = function(root) {
const paths = [];
const dfs = (root, path) => {//Pass in a recursive array of nodes and paths
if (root) {
path += root.val.toString();//Join current node
//The leaf node adds all connected node strings to paths, which is one of the paths
if (root.left === null && root.right === null) {
paths.push(path);
} else {
path += "->"; //Not leaf nodes continue to recurse left and right subtrees
dfs(root.left, path);
dfs(root.right, path);
}
}
}
dfs(root, "");
return paths;
};
java:
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<String>();
dfs(root, "", paths);
return paths;
}
public void dfs(TreeNode root, String path, List<String> paths) {
if (root != null) {
StringBuffer path1 = new StringBuffer(path);
path1.append(Integer.toString(root.val));
if (root.left == null && root.right == null) {
paths.add(path1.toString());
} else {
path1.append("->");
dfs(root.left, path1.toString(), paths);
dfs(root.right, path1.toString(), paths);
}
}
}
}
Method 2:bfs
The animation is too large. Click to view it
- Idea: use queue to assist in breadth first traversal, and constantly add the left and right child nodes to the queue until the leaf node
- Complexity: the same as method 1
js:
var binaryTreePaths = function(root) {
const res = [];
if (root === null) {
return res;
}
const nodes = [root];
const paths = [root.val.toString()];
while (nodes.length) {
const node = nodes.shift();
const path = paths.shift();
if (node.left === null && node.right === null) {//Leaf node
res.push(path);
} else {
if (node.left !== null) {//The left node is not empty and joins the queue
nodes.push(node.left);
paths.push(path + "->" + node.left.val.toString());
}
if (node.right !== null) {//The right node is not empty and joins the queue
nodes.push(node.right);
paths.push(path + "->" + node.right.val.toString());
}
}
}
return res;
};
java:
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> res = new ArrayList<String>();
if (root == null) {
return res;
}
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<String> pathQueue = new LinkedList<String>();
nodeQueue.offer(root);
pathQueue.offer(Integer.toString(root.val));
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.poll();
String path = pathQueue.poll();
if (node.left == null && node.right == null) {
res.add(path);
} else {
if (node.left != null) {
nodeQueue.offer(node.left);
pathQueue.offer(new StringBuffer(path).append("->").append(node.left.val).toString());
}
if (node.right != null) {
nodeQueue.offer(node.right);
pathQueue.offer(new StringBuffer(path).append("->").append(node.right.val).toString());
}
}
}
return res;
}
}
199. Right view of binary tree (medium)
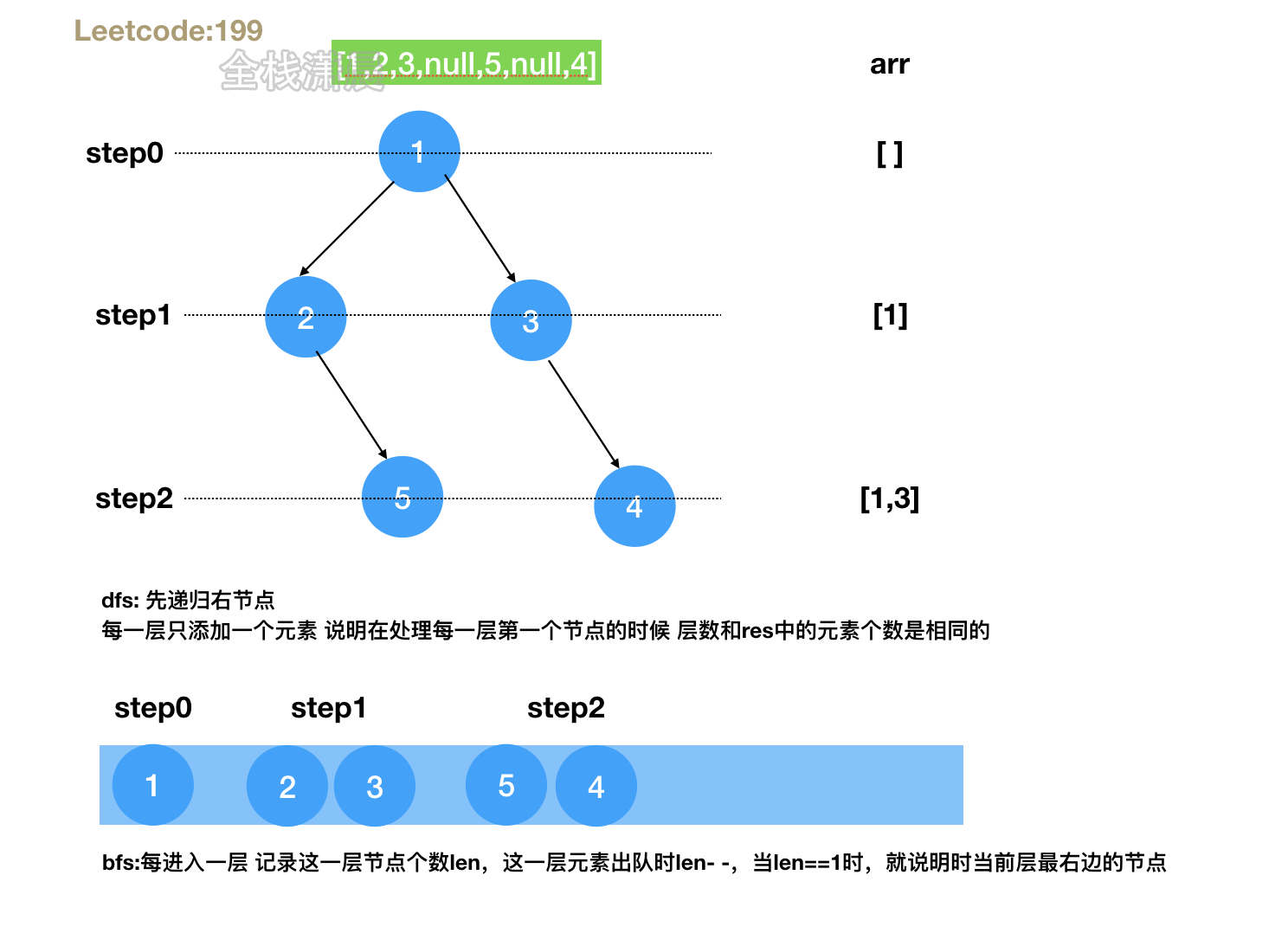
Method 1:dfs
- Idea: depth first traversal. First recurse the right node and let it be processed at the next layer. When the length of res is equal to step, the current node is the right node of this layer and added to the array
- Complexity: the time complexity is O(n), and each node is traversed once. Space complexity O(n), recursive stack space
js:
var rightSideView = function (root) {
function dfs(root, step, res) {//Pass in the number of root node layers and the array of right looking nodes
if (root) {
if (res.length === step) {
res.push(root.val); //When the length of res and step are equal, the current node is the right node of this layer and added to the array
}
dfs(root.right, step + 1, res); //Recurse the right node first and let it be processed first at the next layer
dfs(root.left, step + 1, res);
}
}
if (!root) return [];
let arr = [];
dfs(root, 0, arr);
return arr;
};
java:
class Solution {
List<Integer> res;
public List<Integer> rightSideView(TreeNode root) {
res = new LinkedList<>();
if (root == null) {
return res;
}
dfs(root, 0);
return res;
}
private void dfs(TreeNode root, int depth) {
if (root == null) {
return;
}
if (depth == res.size()) {
res.add(root.val);
}
dfs(root.right, depth+1);
dfs(root.left, depth+1);
}
}
Method 2:bfs
- Idea: breadth first traversal, record the number of nodes in each layer, and reduce the length by 1 after leaving the team. When the length of the previous layer is equal to 1, it indicates that it is the edge node.
- Complexity: the time complexity is O(n), and each node is traversed once. Space complexity O(n), space of queue
js:
var rightSideView = function (root) {
if (!root) return [];
let queue = [root]; //The breadth first traversal queue is first added to root
let arr = []; //Store right looking nodes
while (queue.length > 0) {
let len = queue.length;
while (len) {
let node = queue.shift(); //Fetch the first element of the queue
if (len === 1) arr.push(node.val); //When the length of the previous layer is equal to 1, it indicates that it is the outermost node
if (node.left) queue.push(node.left); //Continue adding left and right nodes to the queue
if (node.right) queue.push(node.right);
len--;//After leaving the team, the length of the current layer is reduced by 1
}
}
return arr;
};
java:
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new LinkedList<>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
TreeNode curr = null;
for (int i = 0; i < size; ++i) {
curr = queue.poll();
if (curr.left != null) {
queue.offer(curr.left);
}
if (curr.right != null) {
queue.offer(curr.right);
}
}
res.add(curr.val);//Or in another way of thinking, after the current layer is cycled, the last one out of the team is the rightmost one of the current layer
}
return res;
}
}