1. Title Description

Give you a string containing only '(' and '), and find the length of the longest valid (well formed and continuous) bracket substring.
Example 1:

Input: s = "(()"
Output: 2
Explanation: the longest valid bracket substring is "()"
Example 2:

Input: s = ") ()"
Output: 4
Explanation: the longest valid bracket substring is "() ()"
Example 3:

Input: s = ""
Output: 0

Tips:

0 <= s.length <= 3 * 10^4
s[i] is' ('or')

2. Ideas and codes

1. Violence

Since the longest valid bracket must be an even number, find the valid bracket according to the largest even number interval. When found, the current interval length is the answer.
For example, if the string length is 6, we first find out whether 0-5 are all valid parentheses. If not, let's change the interval length to 4 and find out whether the intervals 0-3, 1-4 and 2-5 are valid. If one is yes, the answer is 4. Otherwise, change the interval length to 2.

class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size() - s.size() % 2;
        //i represents interval length
        for(int i = n; i > 0; i -= 2)
        {
        	//j represents the starting position
            for(int j = 0; j + i <= s.size(); j ++)
            {
            	//Judge whether the bracket array from J to j + i - 1 is legal
                int l = 0, r = 0;
                bool isbreak = false;
                for(int k = j; k < j + i; k ++)
                {
                    if(s[k] == '(') l ++;
                    else r ++;
                    //	break when you find it illegal
                    if(l < r) { isbreak = true; break; }
                }
                // If it is legal, return to the current interval
                if(l == r && !isbreak) return i;
            }
        }
        return 0;
    }
};

Time complexity O ( n 3 ) O(n^3) O(n3), timeout

2. Dynamic programming

Let f[i] represent the length of the longest legal bracket ending with s[i]. Now let's deduce the recurrence formula.
First of all, we know that legal parentheses end with), and f[i] ending with (must be 0.
We are looking at how to calculate f[i] ending with (), and the calculation of f[i] ending with () can be divided into two parts.
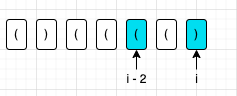
When s[i - 1] = '' and s[i - 1] are '('

When s[i - 1] = = '('), first f[i] = f[i - 2] + 2, and then add the length of the longest legal bracket ending in s[i - 1- 1]. That is, f[i] = f[i - 1] + 2 + f[i - 2]

When s[i -1] = = ')', the situation is complicated

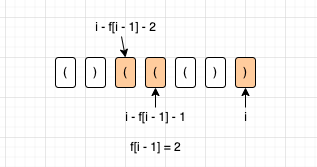
First, we have to see if the "front" is paired with). This front refers to whether the position before the longest legal bracket ending in s[i - 1] is paired with (. If so, the length of f[i] is currently f[i - 1] + 2. Another point to consider is that the length of legal string ending in s[i - f[i - 1] -2] also needs to be added. Therefore, in the case of pairing, f[i] = f[i - 1] + 2 + f[i - f[i - 1] - 2]. In the case of no pairing, the current legal string length ending with s[i] is 0.
Finally, calculate the maximum value of f.

class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size();
        vector<int> f(n + 3,0);
        //In order to avoid crossing the boundary such as i - 2 \ i - f[i - 1] - 1, add a point. Direct judgment is also OK
        s = "  " + s;
        for(int i = 2; i <= n + 1; i ++)
        {
            if(s[i] == '(') continue;
            if(s[i - 1] == '(')  f[i] = f[i - 1] + 2 + f[i - 2];
            else if(s[i - 1] == ')' && s[i - f[i - 1] - 1] == '(') f[i] = 2 + f[i - 1] + f[i - f[i - 1] - 2];
        }
        int ans = 0;
        for(int i = 2; i <= n + 1; i ++)
        {
            ans = max(ans, f[i]);
        }
        return ans;
    }
};

Time complexity O ( n ) O(n) O(n), spatial complexity O ( n ) O(n) O(n)

3. Stack

Using stack is also the method we often use to deal with bracket matching. When s[i] = (when, directly enter the stack and its coordinate I is encountered), pop the stack first. At this time, if the stack is empty, it is proved that it cannot form legal parentheses. At this time, the current I is put on the stack, which means that the next legal bracket can only start from i + 1. If it is not empty, assuming that the element at the top of the stack is k, it means that all parentheses from k + 1 (that is, the next element at the top of the stack) to I are legal.

class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int> st;
        //Now the stack is empty. We need to put - 1 on the stack, indicating that the next legal bracket can only start from 0.
        st.push(-1);
        int ans = 0;
        for(int i = 0; i < s.size(); i ++)
        {
        	//Left parenthesis, directly into the stack
            if(s[i] == '(') st.push(i);
            else {
                st.pop();
                if(st.empty()) st.push(i);
                else ans = max(ans, i - st.top());
            }
        }
        return ans;
    }
};

4. Sweep twice

The idea of scanning twice seems to be the simplest. The only question is why you sweep it twice.
Traverse the string s from left to right, encounter the parenthesis, lnum + +, encounter the right parenthesis rnum + +. When lnum == rnum, update the maximum value. When lnum < rnum, it means that there is an illegal bracket combination, and the previously accumulated lnum and rnum are cleared.
The problem with this method is that the answer will be updated only when lnum == rnum. In such a case (()), the length of () will not be updated. So at this time, we just need to scan it again from right to left, because the answer () will be updated from right to left.

class Solution {
public:
    int longestValidParentheses(string s) {
        int lnum = 0, rnum = 0,ans = 0;
        int n = s.size();
        for(int i = 0; i < n; i ++)
        {
            if(s[i] == '(') lnum ++;
            else rnum ++;

            if(lnum < rnum) lnum = 0, rnum = 0;
            else if(lnum == rnum) ans = max(ans,lnum + rnum);
        }

        lnum = 0, rnum = 0;
        for(int i = n - 1; i >= 0; i --)
        {
            if(s[i] == ')') rnum ++;
            else lnum ++;
            //Note that the scanning conditions should be reversed
            if(lnum > rnum) lnum = 0, rnum = 0;
            else if(lnum == rnum) ans = max(ans,lnum + rnum);
        }
        return ans;
    }
};

reference material

https://leetcode-cn.com/problems/longest-valid-parentheses/solution/zui-chang-you-xiao-gua-hao-by-leetcode-solution/