Title Link: LeetCode interview question 17.21 water volume of histogram

Main idea of the title:

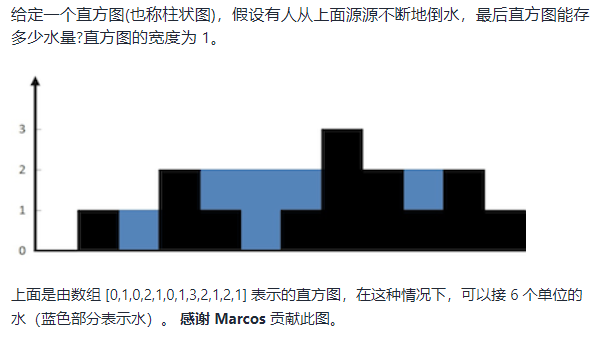
Solution:

dynamic programming

For the subscript \ (I \), the maximum height that the water can reach is equal to the minimum value of the maximum height on both sides of the subscript \ (I \), so you can use dynamic programming to deduce the maximum height on both sides, and then traverse the array. For the subscript \ (I \), the maximum height that the water can reach is equal to the minimum value of the maximum height on both sides of the subscript \ (I \) minus \ (height[i] \).
State transition equation:

class Solution {
public:
    // Dynamic programming calculates the maximum height on both sides
    int trap(vector<int>& height) {
        int n = height.size();
        if (n == 0) {
            return 0;
        }
        vector<int> leftMaxHeight(n);
        leftMaxHeight[0] = height[0];
        for (int i = 1; i < n; ++i) {
            leftMaxHeight[i] = max(leftMaxHeight[i - 1], height[i]);
        }
        vector<int> rightMaxHeight(n);
        rightMaxHeight[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; --i) {
            rightMaxHeight[i] = max(rightMaxHeight[i + 1], height[i]);
        }
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans += min(leftMaxHeight[i], rightMaxHeight[i]) - height[i];
        }
        return ans;
    }
};

Monotone stack

Maintain a monotone stack. The monotone stack stores subscripts, which meet the decrement of elements in the array \ (height \) corresponding to the subscript from the bottom of the stack to the top of the stack.
Traverse the array from left to right. When traversing the subscript \ (I \), if there are at least two elements in the stack, remember that the top element of the stack is \ (top \), and the next element of \ (top \) is \ (left \), there must be \ (height[left] \geq height[top] \). If \ (height [i] > height[top] \), an area that can receive rainwater is obtained. The width of the area is \ (I − left − 1 \) and the height is \ (min(height[left],height[i]) − height[top] \). The amount of water that can be received in the area can be calculated according to the width and height.
After calculating the amount of water that can be received at the subscript \ (i \), put \ (i \) into the stack and continue to traverse the following subscripts to calculate the amount of water that can be received.

class Solution {
public:
    // Monotonic stack subscript, water injection layer by layer
    int trap(vector<int>& height) {
        int ans = 0, n = height.size();
        stack<int> st;
        for (int i = 0; i < n; ++i) {
            while (!st.empty() && height[i] > height[st.top()]) {
                int top = st.top();
                st.pop();
                if (st.empty()) {
                    break;
                }
                int left = st.top();
                int h = min(height[left], height[i]) - height[top];
                int l = i - left - 1;
                ans += l * h;
            }
            st.push(i);
        }
        return ans;
    }
};

Ruler method

Refer to the official solution of LeedCode
In the practice of dynamic programming, two arrays \ (leftMaxHeight \) and \ (rightMaxHeight \) need to be maintained, so the spatial complexity is \ (O(n) \). Can I reduce the space complexity to \ (O(1) \)?
Note that the amount of water that can be connected at the subscript \ (I \) is determined by the minimum of \ (leftMaxHeight[i] \) and \ (rightMaxHeight[i] \). Since array \ (leftMaxHeight \) is calculated from left to right and array \ (rightMaxHeight \) is calculated from right to left, double pointers and two variables can be used instead of two arrays.
Maintain two pointers \ (left \) and \ (right \), and two variables \ (leftMax \) and \ (rightMax \), initially \ (left=0,right=n − 1,leftMax=0,rightMax=0 \). The pointer \ (left \) will only move to the right and the pointer \ (right \) will only move to the left. Maintain the values of two variables \ (leftMax \) and \ (rightMax \) during the movement of the pointer.
When the two pointers do not meet, perform the following operations:

• Update the values of \ (leftMax \) and \ (rightMax \) with the values of \ (height[left] \) and \ (height[right] \);
• If \ (height[left] < height [right] \), there must be \ (leftMax < rightmax \), the amount of water that can be connected at the subscript \ (left \) is equal to \ (leftMax − height[left] \), add the amount of water that can be connected at the subscript \ (left \) to the total amount of water that can be connected, and then add \ (left \) to \ (1 \) (i.e. move one digit to the right);
• If \ (height[left]\geq height[right] \), there must be \ (leftMax \geq rightMax \), and the amount of water that can be connected at the subscript \ (right \) is equal to \ (rightMax − height[right] \), add the amount of water that can be connected at the subscript \ (right \) to the total amount of water that can be connected, and then subtract \ (right \) by \ (1 \) (i.e. move one bit to the left).

When the two pointers meet, the total amount of water that can be connected can be obtained.

class Solution {
public:
    // Double pointer
    int trap(vector<int>& height) {
        int ans = 0, left = 0, right = height.size() - 1, leftMax = 0, rightMax = 0;
        while (left < right) {
            leftMax = max(leftMax, height[left]);
            rightMax = max(rightMax, height[right]);
            if (height[left] < height[right]) {
                ans += leftMax - height[left];
                left++;
            } else {
                ans += rightMax - height[right];
                right--;
            }
        }
        return ans;
    }
};