1, Title Description

The existing method rand7 can generate uniform random integers in the range of 1 to 7. Try to write a method rand10 to generate uniform random integers in the range of 1 to 10.

Do not use the system's math Random() method.

Example 1:
 input: 1
 output: [7]
Example 2:
 input: 2
 output: [8,4]
Example 3:
 input: 3
 output: [8,1,10]

Tips: rand7 is already defined. Pass in parameter: n indicates the number of calls to rand10.

Advanced: What is the expected number of rand7() calls? Can you call rand7() as little as possible?

2, Problem solving ideas

1. Implementing rand4() with rand2()

Assuming that rand2() can uniformly generate [1,2] random numbers, how should we consider if we want to uniformly generate [1,4] random numbers?

I think if you're like me when you're first exposed to this problem, you'll probably think about it like this - add the two rand2() and do some necessary corner processing. As follows:

rand2() + rand2() = ? ==> [2,4]
   1    +   1     = 2
   1    +   2     = 3
   2    +   1     = 3
   2    +   2     = 4
// In order to reduce the range of generating random numbers to [1,n], subtract 1 from the result of the previous step
(rand2()-1) + rand2() = ? ==> [1,3]
   0       +   1     = 1
   0       +   2     = 2
   1       +   1     = 2
   1       +   2     = 3

It can be seen that the fatal point of the results processed by this method is that the results generated are not equal probability. In this simple example, the probability of generating 2 is 50%, while the probability of generating 1 and 3 is 25%, respectively. Of course, the reason is also well understood. Because some values will have multiple combinations, the result will not be equal probability only by simple addition processing.

Therefore, we need to consider other methods.

Carefully observe the above example. We try to multiply (rand2()-1) by 2. The changes are as follows:

(rand2()-1) × 2 + rand2() = ? ==> [1,3]
   0            +   1     = 1
   0            +   2     = 2
   2            +   1     = 3
   2            +   2     = 4

Magical things happened and strange knowledge increased. Through such processing, the result is just the range of [1,4], and each number is obtained with equal probability. Therefore, using this method, rand4() can be implemented through rand2().

Maybe it's just my luck, not universal? Then try a few more examples. For example:

(rand9()-1) × 7 + rand7() = result
     a               b

For convenience, rand9()-1 is now expressed as a and rand7() is expressed as b. The calculation process is expressed as a two-dimensional matrix as follows:

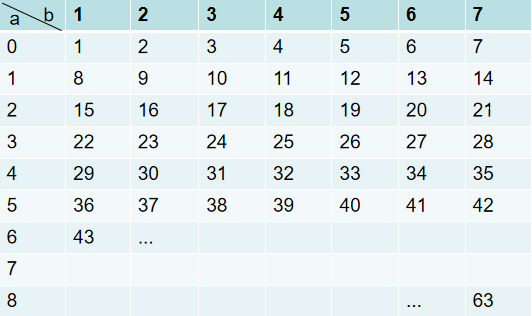
It can be seen that this example can generate random numbers in the range of [1,63] with equal probability. Refining it again, we can get such a law:

Known rand_N() It can be generated with equal probability[1, N]Random number of range
 Then:
(rand_X() - 1) × Y + rand_Y() ==> It can be generated with equal probability[1, X * Y]Random number of range
 That is, it is realized rand_XY()

2. rand2() is implemented with rand4()

So what about rand2() through rand4()? This is very simple. It is known that rand4() will uniformly generate random numbers of [1,4]. It is OK to take the remainder and add 1. As shown below, the result is also equal probability.

rand4() % 2 + 1 = ?
   1 % 2    + 1 = 2
   2 % 2    + 1 = 1
   3 % 2    + 1 = 2
   4 % 2    + 1 = 1

In fact, as long as Rand_ If N in N () is a multiple of 2, it can be used to realize rand2(). On the contrary, if N is not a multiple of 2, the result is not equal probability. For example:

rand6() % 2 + 1 = ?
   1 % 2    + 1 = 2
   2 % 2    + 1 = 1
   3 % 2    + 1 = 2
   4 % 2    + 1 = 1
   5 % 2    + 1 = 2
   6 % 2    + 1 = 1

rand5() % 2 + 1 = ?
   1 % 2    + 1 = 2
   2 % 2    + 1 = 1
   3 % 2    + 1 = 2
   4 % 2    + 1 = 1
   5 % 2    + 1 = 2

3. rand10() is implemented with rand7()

ok, now return to this topic. It is known that rand7() requires rand10() to be implemented through rand7().

With the previous analysis, to implement rand10(), you need to implement Rand first_ N (), and ensure that n is greater than 10 and a multiple of 10. Then through rand_N()% 10 + 1 can get the random number in the range of [1,10].

And implement rand_N(), we can modify rand7() by the method described in part 1, as follows:

(rand7()-1) × 7 + rand7()  ==> rand49()

But the N realized in this way is not a multiple of 10! What should I do? This involves the knowledge of "reject sampling", that is, if a sampling result is not within the required range, it will be discarded. Based on the above analysis and looking back at the following code, it must not be difficult to understand.

class Solution extends SolBase {
    public int rand10() {
        while(true) {
            int num = (rand7() - 1) * 7 + rand7(); // Generating random numbers in the range of [1,49] with equal probability
            if(num <= 40) return num % 10 + 1; // Reject sampling and return a random number in the [1,10] range
        }
    }
}