Catalogue of series articles
I Array type problem solving method 1: dichotomy
II Array type problem solving method 2: Double finger needle method
III Array type problem solving method 3: sliding window
IV Array type problem solving method 4: simulation
V The basic operation and classic topics of the linked list
Vi Classic title of hash table
VII Classic title of string
VIII KMP of string
IX Solution: double pointer
X Classic title of stack and queue
Xi top-K problem in stack and queue
XII The first, middle and last order traversal of binary tree
XIII Sequence traversal of binary tree and related topics
XIV Binary tree part of binary tree attributes related topics
XV Modification and construction of binary tree in binary tree chapter
XVI Properties of binary search tree
XVII The problem of common ancestor in binary tree discourse
XVIII Modification and construction of binary search tree in binary tree chapter
XIX Combinatorial problem of backtracking algorithm
XX The algorithm of the whole subset
XXI Introduction to greedy algorithm
XXII Advanced problem of greedy algorithm
Updating
preface
The question brushing route comes from: Code Capriccio
Every state in dynamic programming must be derived from the previous state, such as frog jumping step, and the nth step jumps up from N-1 or N-2 step.
Problem solving steps:
- Status (dp array and meaning of subscript)
- Recursive formula and cyclic structure
- initialization
- Return value
Inscription
509. Fibonacci number
Leetcode link

Solution:
Method 1: recursion
class Solution {
public int fib(int n) {
if (n == 0 || n == 1) return n;
return fib(n - 1) + fib(n - 2);
}
}
Mode 2: dynamic programming
class Solution {
public int fib(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
Space optimization:
class Solution {
public int fib(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
int a = 0;
int b = 1;
int res = 0;
for (int i = 2; i <= n; i++) {
res = a + b;
a = b;
b = res;
}
return res;
}
}
70. Climb stairs
Leetcode link

Solution:
The nth floor stairs jump up from the N - 1 or N - 2 floor
dp array
class Solution {
public int climbStairs(int n) {
if (n == 1) return 1;
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
746. Use the minimum cost to climb stairs
Leetcode link
Give you an integer array cost, where cost[i] is the cost of climbing up the ith step of the stairs. Once you pay this fee, you can choose to climb up one or two steps.
You can choose to climb the stairs from the steps with subscript 0 or subscript 1. Please calculate and return the minimum cost to reach the top of the stairs.

Solution:
class Solution {
public int minCostClimbingStairs(int[] cost) {
int len = cost.length;
int[] dp = new int[len];
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < len; i++) {
dp[i] = Math.min(dp[i - 1], dp[i - 2]) +cost[i];
}
return Math.min(dp[len - 1], dp[len - 2]);
}
}
62. Different paths
Leetcode link
A robot is located in the upper left corner of an m x n grid (the starting point is marked "Start" in the figure below). The robot can only move down or right one step at a time. The robot attempts to reach the lower right corner of the grid (marked "Finish" in the figure below). How many different paths are there altogether?
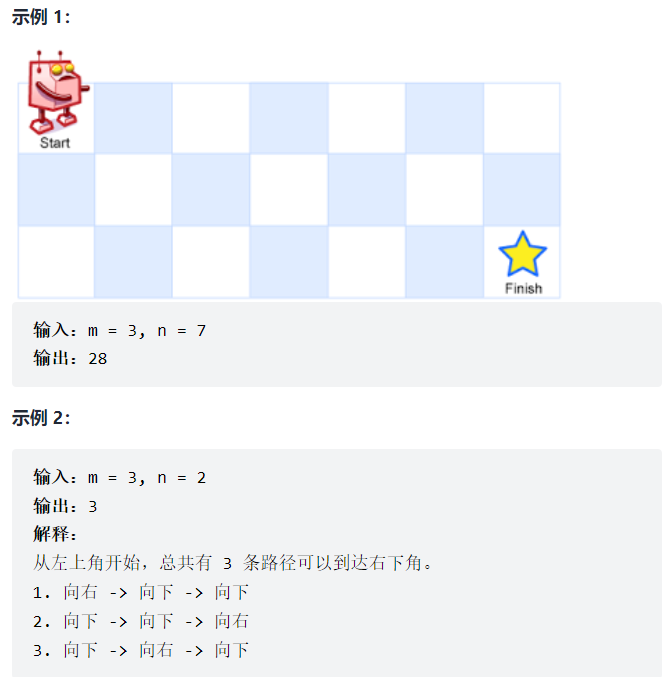
Solution:
Status (i, j): number of paths from (0, 0) to (i, j)
Equation of state: F(i,j) = F(i-1,j) + F(i,j-1)
Initial state: F(0,0) = F(0,j) = F(i,0) = 1
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int i = 0; i < n; i++) dp[0][i] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n- 1];
}
}
Optimization:
Status (i,j): number of paths from (0, 0) to (i,j)
Equation of state: F(i,j) = F(i-1,j) + F(i,j-1)
Initial state: F(0,j) = F(i,0) = 0, F(0,1) = 1 or F(1,0) = 1
Return result: F(row,col)
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m + 1][n + 1];
dp[0][1] = 1;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
}
63. Different paths II
Leetcode link
A robot is located in the upper left corner of an m x n grid (the starting point is marked "Start" in the figure below). The robot can only move down or right one step at a time. The robot attempts to reach the lower right corner of the grid (marked "Finish" in the figure below). Now consider that there are obstacles in the grid. So how many different paths will there be from the upper left corner to the lower right corner? The obstacles and empty positions in the grid are represented by 1 and 0 respectively.
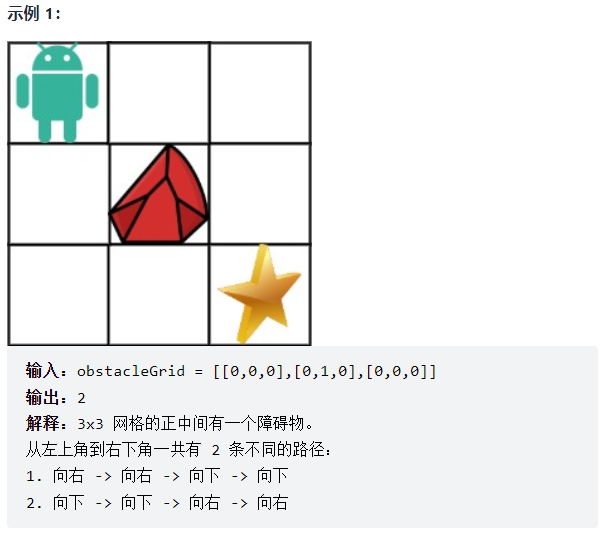
Solution:
As above, change the initial state. When the first row and the first column encounter stones, the back will also be initialized to 0, and only the place with stones in the middle area will be 0
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int row = obstacleGrid.length;
int col = obstacleGrid[0].length;
int[][] dp = new int[row][col];
for (int i = 0; i < row && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < col && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
if (obstacleGrid[i][j] == 0) {
dp[i][j] = dp[i - 1][j] + dp[i][j -1];
} else {
dp[i][j] = 0;
}
}
}
return dp[row - 1][col - 1];
}
}
Optimization:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int row = obstacleGrid.length;
int col = obstacleGrid[0].length;
int[][] dp = new int[row + 1][col + 1];
dp[0][1] = 1;
for (int i = 1; i <= row; i++) {
for (int j = 1; j <= col; j++) {
if (obstacleGrid[i - 1][j - 1] == 1) {
dp[i][j] = 0;
}else {
dp[i][j] = dp[i][j - 1] + dp[i -1][j];
}
}
}
return dp[row][col];
}
}
53. Maximum subarray and
Leetcode link
Give you an integer array nums. Please find a continuous sub array with the largest sum (the sub array contains at least one element) and return its maximum sum. A subarray is a contiguous part of an array.

Solution:
Status dp[i]: calculate the sum of the longest continuous subarray at position i
Equation of state: DP [i] = math max(dp[i - 1] + nums[i], nums[i])
Return value: maxSum during traversal
class Solution {
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
int maxSum = nums[0];
dp[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
maxSum = Math.max(dp[i], maxSum);
}
return maxSum;
}
}
343. Integer splitting
Leetcode link
Given a positive integer n, split it into the sum of K positive integers (k > = 2) and maximize the product of these integers. Returns the maximum product you can obtain.

Solution:
Example: 5 can be decomposed into 1 + 4, 2 + 3, 3 + 2 and 4 + 1
dp[1] * 4, dp[2] * 3, dp[3] * 2, dp[4] * 1. But there is no maximum here
dp[2] = 1 * 1 = 1, dp[3] = 1 * 2 = 2, maximum dp[3] * 2 = 4
The largest is 6:5 = 2 + 3, 2 * 3 = 6
For larger numbers, the recursive formula is satisfied, so the recursive formula includes: math max(dp[j] * (i - j), j * (i - j))
Status dp[i]: split maximum product of integer I
Equation of state: math max(dp[i], Math.max(dp[j] * (i - j), j * (i - j)));
It can also be understood that j * (i - j) simply divides an integer into two numbers and multiplies, while j * dp[i - j] is divided into two or more numbers and multiplies.
Initialization: because k > = 2, dp[2] = 0
Return: dp[n]
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[2] = 1;
for (int i = 3; i <= n; i++) {
for (int j = 1; j <= i - 1; j++) {
dp[i] = Math.max(dp[i], Math.max(dp[j] * (i - j), j * (i - j)));
}
}
return dp[n];
}
}
96. Different binary search trees
Leetcode link
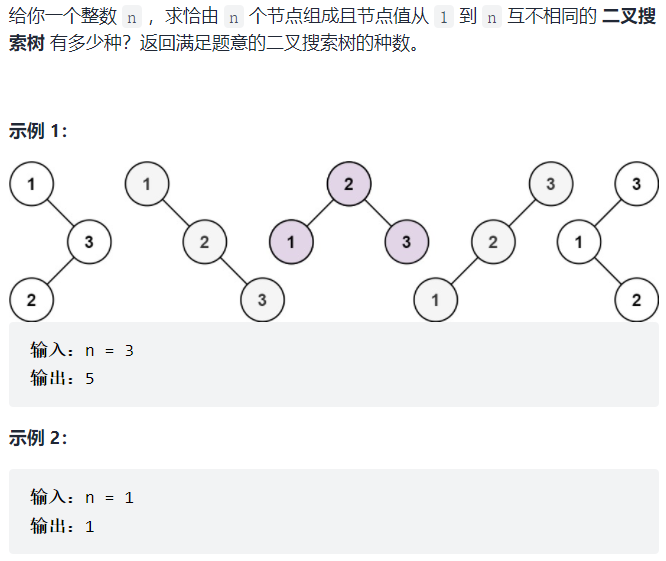
Solution:
i is expressed as n
J means that j is the root node
For example, when i = 3, j is 1, 2 and 3 respectively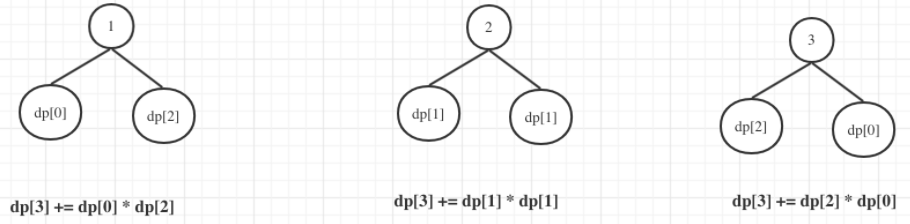
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j- 1] * dp[i - j];
}
}
return dp[n];
}
}