I have encountered a lot of monotonous stack problems when I brush questions recently. I hereby record it. I forget it all in the future.
The monotone stack problem has a feature that most of the stack does not store elements directly, but subscripts, which are used to judge.
Monotone stack, as the name suggests, means that the elements stored in the stack are non increasing or non decreasing, which is convenient for traversal

Q1 LeetCode739 daily temperature

Please regenerate a list according to the daily temperature list temperatures. The output of its corresponding position is required to be: at least the number of days to wait for higher temperatures. If the temperature will not rise after that, please replace it with 0 in this position.

Example 1:
Input: temperatures = [73,74,75,71,69,72,76,73]
Output: [1,1,4,2,1,1,0,0]

Idea:

This problem requires the number of days with the nearest high temperature to the day. Of course, it can be solved directly, but the time complexity is n^2, but the time complexity can be reduced to N by using monotone stack. In fact, there is a way to judge whether to use monotone stack. If the first one on the left or right is required to be larger or smaller than the current position, you can consider using monotone stack.

code:

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        Deque<Integer> q = new LinkedList<>();
        int[] res = new int[temperatures.length];
        for(int i=0;i<res.length;i++){
        //This while statement means that as long as the current element is greater than the top element of the stack,
        //Then, while modifying the result array, take it out of the stack and execute it repeatedly.
        //Because what can be pushed into the stack must be smaller than the element at the bottom of the stack,
        //So stop until it is judged that the element in the stack is larger than the current element or the stack is empty, and then push the element into the stack
            while(!q.isEmpty() && temperatures[i]>temperatures[q.peek()]){
                res[q.peek()]=i-q.peek();
                q.pop();
            }
            q.push(i);
        }
        return res;
    }
}

Q2 maximum rectangular area of leetcode84 histogram

Given the nonnegative integer array heights, the numbers in the array are used to represent the height of each column in the histogram. Each column is adjacent to each other and has a width of 1.
Find the maximum area of the rectangle that can be outlined in the histogram.

Example 1:

Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: the largest rectangle is the red area in the figure, with an area of 10

Idea:

This question is more difficult than the daily temperature, but in the final analysis, finding the largest rectangle is actually finding the first position on the left and right of the current position that is smaller than the current value. Because if both the left and right sides are larger than the current position, the area of the rectangle will be calculated according to the height of the current position, and the width is the subscript value of right left. Traverse the heights array in turn, and then return max
The two arrays maintained represent the first subscript on the left and right that is less than the current value
And don't forget to initialize the right boundary!!! It is very important because there may be a situation where the value of a certain position is not smaller than it. Therefore, at this time, its area is the length of the whole array. Therefore, during initialization, the left boundary should be initialized to 0 and the right boundary should be initialized to n. This will solve the problem

code:

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        int[] left = new int[len];
        int[] right = new int[len];
        Arrays.fill(right,len);
        Deque<Integer> q = new LinkedList<>();
        for(int i=0;i<len;i++){
            while(!q.isEmpty()&&heights[i]<heights[q.peek()]){
                right[q.peek()]=i;
                q.pop();
            }
            left[i]=q.isEmpty()?-1:q.peek();
            q.push(i);
        }
        int max=0;
        for(int i=0;i<len;i++){
            max=Math.max(max,heights[i]*(right[i]-left[i]-1));
        }
        return max;
    }
}

Q3 LeetCode40 connected to rainwater

Given n non negative integers to represent the height diagram of each column with width of 1, calculate how much rain the columns arranged according to this can receive after raining.

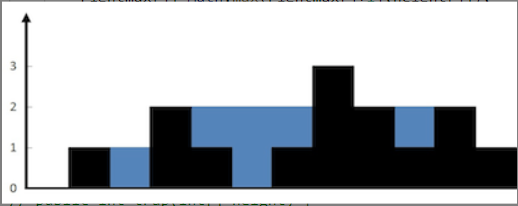
Example 1:
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: the above is the height map represented by the array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rainwater can be connected (the blue part represents rainwater)

Idea:

This question is actually similar to the previous one, but the last one is to find the low on both sides, because it is necessary to calculate the area, while this question is to find the high on both sides. The main idea is to refer to Q2. But if you use a monotone stack for this problem, it's better to directly use double pointers or directly maintain two arrays, so you don't need a monotone stack.
Therefore, when using the monotone stack, you can actually change your thinking. Similarly, the monotone stack stores decreasing data, which means that if there are at least two elements in the stack, the top element of the stack is smaller than the previous element. At this time, if the value of the current position traversed is also larger than the top of the stack, it forms a high-low shape, that is, it can receive rainwater

code:

class Solution {
    public int trap(int[] height) {
        int ans = 0;
        Deque<Integer> stack = new LinkedList<Integer>();
        int n = height.length;
        for (int i = 0; i < n; ++i) {
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                int top = stack.pop();
                if (stack.isEmpty()) {
                    break;
                }
                int left = stack.peek();
                int currWidth = i - left - 1;
                int currHeight = Math.min(height[left], height[i]) - height[top];
                ans += currWidth * currHeight;
            }
            stack.push(i);
        }
        return ans;
    }
}