leetcode notes

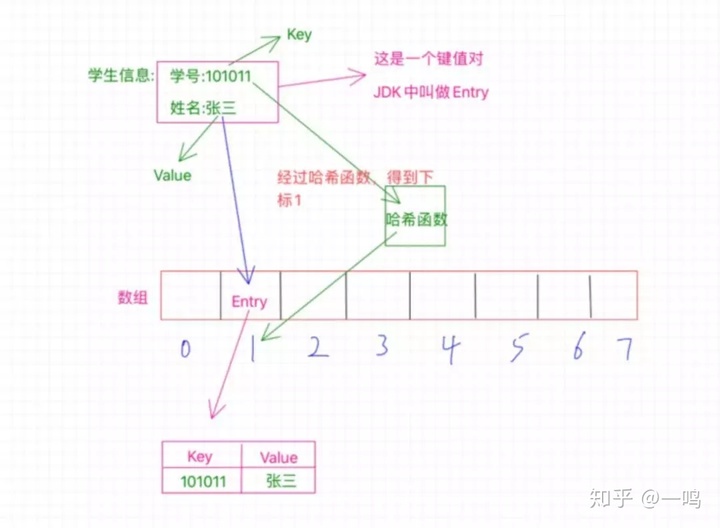
1.Hash related

When using HashMap, why can you find the corresponding value according to map.get(key) with time complexity O(1)?

Because the physical structure uses a hash table

Calculate the array position where the Entry should be stored according to a special algorithm. If the positions are the same, there are various methods to solve the conflict and find the value after the conflict

Press button T387 to find the first non repeating character of the string and return its index

Using hash, value can put all kinds of things, such as the position of the first occurrence. If it occurs many times, it will be set to - 1. Hash storage is not sequential, but it can be found as quickly as possible, O(1)
q49 letter ectopic word grouping

The meaning of the title is to group the abc,bac,cab... Of the string array

When this type thinks of hash, it first thinks of what is the key and what is the value

Keys are unique. The only common point of the same group is that their letters and times are unique, but their positions are different. This is the most key point in solving problems
1. Alphabetical as key
2. The number of times the same letter appears as the key
Knowledge points:
1. String key = String(array) is better than String.valueOf(array) is better than array.toString
  - valueOf can prevent the array from being null, but it will be converted to the string "null"
2. Many types of conversions cannot be forced. Generally, new is a required type, and then new is added at the same time
Subarray with q560 and K

Hash + sub prefix method. In the hash array, the key stores the sum of all arrays from the beginning to this position in the traversal process, and value is the number of occurrences

Pre is the sum of all previous elements, from j to I = > pre [j − 1]==pre[i] − k

For example, if the sum of the first six elements is 14 and the goal is to find 7, then map.get(14-7) to see how many elements meet the sum of 7 from the beginning to a certain location

[external link image transfer failed. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-gxx8vv50-1637714619647) (C: / users / chenzhijian / appdata / roaming / typora / typora user images / image-20211111202134415. PNG)]
```
public int subarraySum(int[] nums, int k) {
    int count = 0;
    Map<Integer, Integer> map = new HashMap<>();
    map.put(0 ,1);
    int pre = 0;
    for (int i = 0; i < nums.length; i++) {
        pre += nums[i];
        if (map.containsKey(pre - k)) {
            count+=map.get(pre - k);
        }
        map.put(pre, map.getOrDefault(pre, 0) + 1);
    }
    return count;
}
```

2. Linked list operation

Force buckle T19, traverse and delete the penultimate node of the linked list

Pay attention to the special case of deleting the head node

Force buckle T206 reverse linked list

The most common method is to use the iterative method of three pointers (including head pointer) to save the front and rear nodes with pointers. Pay attention to prevent null pointer exception when defining multiple pointers at the beginning

if(head == null || head.next == null){
    return head;
}

This is not too stupid, so you don't have to judge with a non null pointer

ListNode pre = null, p = head;
while (p != null) {
    ListNode next = p.next;
    p.next = pre;
    pre = p;
    p = next;
}
return pre;

Recursive methods are difficult to understand

public ListNode reverseList(ListNode head) {

    //Recursive exit. This head==null prevents the ListNode linked list provided from being empty and should be written in front to prevent null pointer exceptions
    if (head == null || head.next == null){
        return head;
    }

	//This newHead has not changed from beginning to end. It is the first node of the result
    ListNode newHead = reverseList(head.next);
    head.next.next = head;
    head.next = null;

    return newHead;
}

Force buckle T61 rotation linked list (right translation linked list)

At the beginning, inspired by the reverse linked list, I wrote a method to reverse the linked list, which was done by translating the array. However, the code is very complex, and it is prone to null pointers and linked list ring exceptions. After looking at the force buckle solution, I originally made the linked list ring and then disconnected. Can I define three more pointers and traverse the method only once
Sword fingers t25 merge two sorted linked lists

You can use the recursive method to understand the idea of recursion through this question
Copy of sword finger t35 complex linked list
1. Method with high time complexity
  1. Copy the trunk first
  2. Find the point pointed by the pointer from scratch, complexity O(n ²)
2. Trade space for time
  1. Store the corresponding relationship between the original node and the node in the map
  2. Copying pointers through relationships
```
while(cur != null) {
            map.get(cur).next = map.get(cur.next);
            map.get(cur).random = map.get(cur.random);
            cur = cur.next;
        }
```
Q442 returns the first node of the ring linked list

The simplest way is to store each node in the hashset, and the repeated answer is the answer

If O(1) space is required, the mathematical column formula is deduced

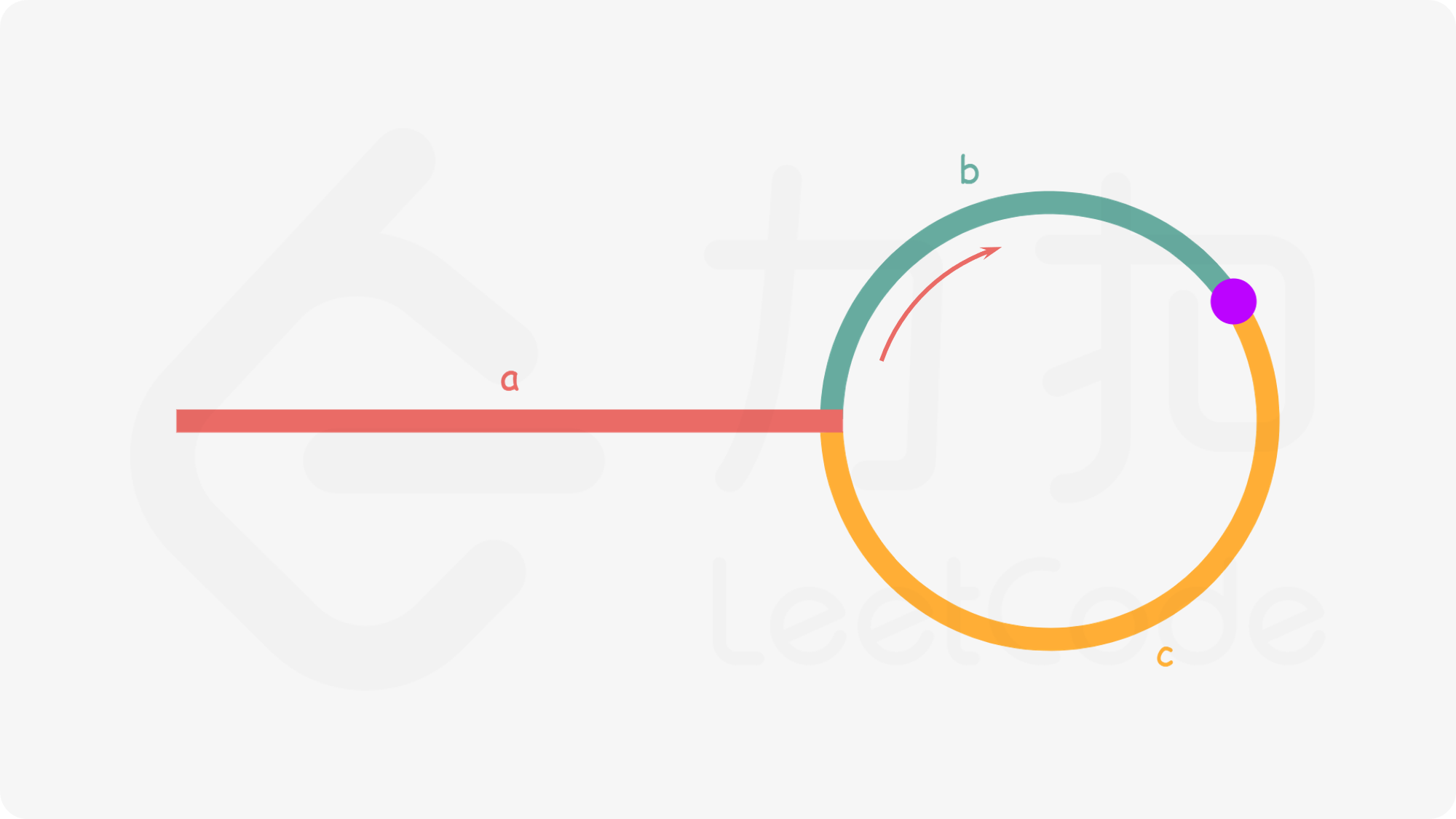
a+n(b+c)+b=a+(n+1)b+nca+n(b+c)+b=a+(n+1)b+nc

a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)

When we find that slow meets fast, we use an additional pointer ptr. At first, it points to the head of the linked list; then, it and slow move back one position at a time. Finally, they will meet at the entry point
```
// Fast! = null cannot be used as the condition here. There may not be a ring
while (fast != null) {
    slow = slow.next;
    if (fast.next != null) {
        fast = fast.next.next;
    } else {
        return null;
    }
    if (fast == slow) {
        ListNode p = head;
        while (p != slow) {
            p = p.next;
            slow = slow.next;
        }
        return p;
    }
}
```

LRU caching mechanism

You are required to encapsulate a class. You need to use a hash table and a two-way linked list. In fact, java has a similar data structure, LinkedHashMap

The hash table is used to quickly find the nodes in the two-way linked list. The latest inserted or found nodes are placed at the head of the two-way linked list. If the space is full, the nodes in the tail will be eliminated. It is very convenient to use pseudo head and pseudo tail nodes

I just don't understand how this class can be defined like this. The foundation is not good

There are two things I didn't consider

Get the value from the map through the key. What if the new put node exists
After deleting nodes from the list, the nodes in the corresponding map should also be deleted

public class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int _key, int _value) {
            key = _key;
            value = _value;
        }
    }

    private int size;
    private int capacity;
    private Map<Integer, DLinkedNode> cache = new HashMap<>();
    private DLinkedNode head;
    private DLinkedNode tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        // Use hashmap to determine whether there is
        if (cache.containsKey(key)) {
            // Find the corresponding node of DLinkedNode through hashmap
            DLinkedNode node = cache.get(key);
            // Move the node to the header
            moveToHead(node);
            return node.value;
        } else {
            return -1;
        }
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // Put it into hashmap first
            DLinkedNode newNode = new DLinkedNode(key, value);
            cache.put(key, newNode);
            // Determine whether it is full
            if (size == capacity) {
                DLinkedNode tail =  removeTail();
                cache.remove(tail.key);
                size--;
            }
            addToHead(newNode);
            size++;
        }
        else {
            node.value = value;
            moveToHead(node);
        }
    }
    ...
}

q148 sorting linked list

Analysis: the sorting time complexity of O(nlogn) includes fast, hope, return and heap. Only merge sorting conforms to the linked list. Top-down recursive merge is simpler, but the space complexity depends on the stack space of recursive call. Bottom-up recursion can achieve O(1)

recursion

Recursion before merging

Odd nodes find the midpoint, even nodes find the node on the left of the center, and then cut off from the back

The combination uses to create a pseudo head node first, and the smaller of the two linked lists will be followed by it

public ListNode sortList(ListNode head) {
    if (head == null || head.next == null) {
         return head;
    }
    // Find the middle point through the fast and slow pointer
    ListNode slow = head, fast = head.next;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    ListNode tmp = slow.next;
    slow.next = null;
    ListNode lHead = sortList(head);
    ListNode rHead = sortList(tmp);
    
    // merge
    ListNode nHead = merge(lHead, rHead);
    return nHead;
}

private ListNode merge(ListNode p, ListNode q) {
    ListNode fakeHead = new ListNode(0);
    ListNode temp = fakeHead;
    while (p != null && q != null) {
        if (p.val <= q.val) {
            temp.next = p;
            p = p.next;
        } else {
            temp.next = q;
            q = q.next;
        }
        temp = temp.next;
    }
    if (p != null) {
        temp.next = p;
    } else {
        temp.next = q;
    }

    return fakeHead.next;
}

Iteration is really complex, and the details are difficult to grasp

Use the for (int sublength = 1; sublength < length; sublength < < = 1) cycle. In the first cycle, each group has one node, which is to split all the nodes in the linked list, sort left and right and merge them into two groups. In the second cycle, each group has two nodes, and then sort and merge them into four or four groups

Do it later

q160 intersecting linked list

There are many ways
1. First get the long length - the short length a, the long pointer goes the length a, and then go together
2. Store the nodes in hashset
3. A's individual length m, B's individual length N, and the common length C. If a can't complete the interaction to B, B can't complete the interaction to a, then it is empty at the same time. m+c+n = n+c+m
```
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    if(headA == null || headB == null) {
        return null;
    }
    ListNode p = headA, q = headB;
    while (p != q) {
        p = p == null ? headB : p.next;
        q = q == null ? headA : q.next;
    }
    return p;
}
```

q234 palindrome linked list

If the time complexity is not limited, you can directly copy the linked list into the array and then judge

Limit the time complexity to O(1). First find the midpoint through the fast and slow pointer, and then reverse and compare the subsequent linked list. If the original structure cannot be changed, reverse and restore again

public boolean isPalindrome(ListNode head) {
    if (head == null) {
        return true;
    }
    // The speed pointer finds the midpoint
    ListNode slow = head;
    ListNode fast = head;
    while (fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    ListNode newHead = reverse(slow.next);
    ListNode p1 = head;
    ListNode p2 = newHead;
    // p2.length == p1 or p1-1
    while (p2 != null) {
        if (p1.val != p2.val) {
            return false;
        }
        p1 = p1.next;
        p2 = p2.next;
    }
    return true;
}

// Operation method of transferring linked list
private ListNode reverse(ListNode head) {
    ListNode curr = head;
    ListNode prev = null;
    while (curr != null) {
        ListNode temp = curr.next;
        curr.next = prev;
        prev = curr;
        curr = temp;
    }
    return prev;
}

Copy of sword finger t35 complex linked list

Connect the old and new nodes through map

if (head == null) {
    return null;
}
Node node = head;
Map<Node, Node> map = new HashMap<>();
while (node != null) {
    Node newNode = new Node(node.val);
    map.put(node, newNode);
    node = node.next;
}
node = head;
Node newHead = map.get(head);
while (node != null) {
    Node newNode = map.get(node);
    newNode.next = map.get(node.next);
    newNode.random = map.get(node.random);
    node = node.next;
}
return newHead;

Recursive writing of method 1

if (!map.containsKey(head)) {
    Node newHead = new Node(head.val);
    map.put(head, newHead);
    newHead.next = copyRandomList(head.next);
    newHead.random = copyRandomList(head.random);
}
return map.get(head);

Method 2: connect them together and then disassemble them

// New and connect
for (Node p = head; p != null; p = p.next.next) {
    Node node = new Node(p.val);
    node.next = p.next;
    p.next = node;
}
// Find random pointer position
for (Node p = head; p != null; p = p.next.next) {
    if (p.random != null) {
        p.next.random = p.random.next;
    }
}
// separate
Node newHead = head.next;
for (Node p = head, q = newHead; p != null; p = p.next, q = q.next) {
    p.next = q.next;
    if (p.next != null) {
        q.next = p.next.next;
    }
}
return newHead;

3. Double pointer

When we need to enumerate two elements in the array, if we find that the second element decreases with the increase of the first element, we can use the double pointer method to reduce the time complexity of enumeration from O(N^2) to O(N)

q11 container with the most water

I thought that the simple method was just to walk in at the same time. If you encounter a shorter jump, you can walk in at the same time
q15 sum of three numbers

After a few hours, there are still various problems... The violence method needs a triple loop. If you use double pointers, the time complexity can be reduced to O(n) ²), Under the second for loop, the right pointer only needs to move to the left (the first for loop needs to update the right pointer to the rightmost every time). As long as we consider the traversal process of the first two pointers, we should pay attention to some problems: the order of the three pointers cannot be changed. If two identical numbers are together, we should skip the first for loop.

We also encountered an empty array exception similar to the null pointer exception. Before writing num [I-1], we must ensure that I > 0 is written to its left
```
if(i>0 && nums[i] == nums[i-1])
```
q16 the sum of the three closest trees

It is similar to the previous question, but I accidentally wrote it into a triple cycle. It is also similar to q11. Temporarily fix the first one, the other two go to the middle, and the first one goes back
The penultimate node in the sword finger t22 lin k ed list (pay attention to robustness)
1. The linked list cannot be empty
2. k will not 0
3. k is not greater than the length of the linked list
Find the first node of the link in the linked list
1. The fast and slow pointer finds the first node where the pointer meets first
2. The number of nodes in the ring is calculated from this node
3. In the double pointer, the previous pointer first goes through the nodes of the loop and then steps together until it meets
Q441 circular linked list
1. In the Hash table method, it can store linked list nodes directly, not only numbers. It is more convenient to use HashSet here, because repeated storage will directly false, which is less than ArrayList
2. Tortoise and rabbit race
  
  However, for fast and slow pointers, pay more attention to null pointer exceptions. You should not only judge at the beginning, but also judge whether the fast pointer has reached the tail node or whether the next pointer has reached the tail node

q438 find all letter words in the string

sliding window

Because the characters in the string are all lowercase letters, an array with a length of 26 can be used to record the number of letters
Let n = len(s), m = len §. Record the letter frequency p_cnt of the P string and the frequency s_cnt of the first m letters of the s string
If p_cnt and s_cnt are equal, the first ectopic word index 0 is found
Continue to traverse the letter of s string index [m, n), add a new letter in s_cnt each time, and remove an old letter
Judge whether p_cnt and s_cnt are equal. If they are equal, add an ectopic word index i - m + 1 in the return value res

public List<Integer> findAnagrams(String s, String p) {
    List<Integer> list = new ArrayList<>();
    int n = s.length();
    int m = p.length();
    // This situation has been forgotten
    if (n < m) {
        return list;
    }
    int[] sArr = new int[26];
    int[] pArr = new int[26];
    for (int i = 0; i < m; i++) {
        sArr[s.charAt(i) - 'a'] += 1;
        pArr[p.charAt(i) - 'a'] += 1;
    }
    if (Arrays.equals(sArr, pArr)) {
        list.add(0);
    }
    for (int i = m; i < n; i++) {
        sArr[s.charAt(i-m) - 'a'] -= 1;
        sArr[s.charAt(i) - 'a'] += 1;
        if (Arrays.equals(sArr, pArr)) {
            list.add(i-m+1);
        }
    }
    return list;
}

Double pointer

4. String operation

q14 longest common prefix

Generally, those without systematic training choose vertical brute force cracking, which is compared one by one. However, although my brute force cracking is successful, it is too complex. The subsequent ones only need to be equal to the corresponding characters of the first string. Moreover, the end condition of the first for loop condition can be temporarily subject to the length of the first string. When entering later, judge whether it exceeds this limit String length to compare when

Many test cases are not considered
- Non null judgment
- There is only one element in the array
- Judgment of other situations
There are many ingenious methods to use strings, such as startsWith and substring
```
public String longestCommonPrefix(String[] strs) {
        if(strs.length==0)return "";
        //The common prefix is shorter than all strings. Choose any one first
        String s=strs[0];
        for (String string : strs) {
            while(!string.startsWith(s)){
                if(s.length()==0)return "";
                //If the public prefix does not match, make it shorter!
                s=s.substring(0,s.length()-1);
            }
        }
        return s;
    }
```
q763 divide letter interval

There is an idea that needs to be studied. If you already know that it is a fixed length structure such as letters or numbers, you can directly use the int array: arr[S.charAt(i) - 'a'], so that arr[0] corresponds to a

First get the int array corresponding to the last position of the letter. Judge whether the last position of the letter scanned locally is larger than the current one. If so, update and expand the end condition of the while loop
```
int i=0,k;
while (i < S.length()) {
    k = S.charAt(i)-'a';
    int cur = i;
    while (i<=last[k]){
        if(last[S.charAt(i)-'a']>last[k]){
            k = S.charAt(i)-'a';
        }
        i++;
    }

    list.add(i - cur);
}
```
q6 Z font transformation

The most concise solution is really too brainy. How can you think of something you haven't seen? Let flag participate in the calculation
```
public String convert(String s, int numRows) {
        if(numRows < 2) return s;
        List<StringBuilder> rows = new ArrayList<StringBuilder>();
        for(int i = 0; i < numRows; i++){
        	rows.add(new StringBuilder());
        }
        int i = 0, flag = -1;
        for(char c : s.toCharArray()) {
            rows.get(i).append(c);
            if(i == 0 || i == numRows -1) flag = - flag;
            i += flag;
        }
        StringBuilder res = new StringBuilder();
        for(StringBuilder row : rows) res.append(row);
        return res.toString();
    }
```
At first, I didn't want to define Arraylist. I wanted to use StringBuider array. It was found that if the initial value of the array was null, I couldn't use the. append method. Instead, I changed it to String array, but in the first round, I had to assign an empty String first. Otherwise, if I used "" + c, the first bit would be null and an error would be reported. This can succeed, but the increase or decrease cost of String array is too large. It's not as good as list
The sword finger t17 prints from 1 to the maximum n digits
1. n may be very large. The number type will be removed and the string will be used instead. The large number problem
2. Optimize to quickly determine whether the maximum bit is reached, and use the O(1) method to optimize the output code
3. It should also be noted that the previous zero is not output for the user experience
4. Full Permutation (in doubt)

q3 longest substring without duplicate characters

You can use set and map

//In the sliding window, i is the beginning and end is the end
for (int i = 0; i < len; i++) {
    while (end<len && !occ.contains(s.charAt(end))){
        occ.add(s.charAt(end));
        if((end-i+1)>max){
            max = end-i+1;
        }
        end++;
    }
    occ.remove(s.charAt(i));
}

mistake

If end is ignored before, it will not move forward, and the complexity of full emptying set is high
The length judgment in while should be put in front to prevent crossing the boundary

q394 string encoding

There are many details about stack operation, but it's not difficult to understand. When you encounter '[' into the stack, when you encounter ']', start decoding this paragraph. See the notes for details

Summary:

StringBuilder can easily operate a single character without defining a large collection
Character.isLetter is the api to determine whether it is a character

public String decodeString(String s) {
    // Scan it first and put it on the stack except ']'
    Stack<Character> stack = new Stack<>();
    for (char c : s.toCharArray()) {
        if (c != ']') {
            stack.push(c);
        } else {
            //Find letter position
            StringBuilder sb = new StringBuilder();
            while (!stack.isEmpty() && Character.isLetter(stack.peek())) {
                sb.insert(0, stack.pop());
            }
            stack.pop(); // Remove '['
            String sub = sb.toString();
            //Find digit
            sb = new StringBuilder();
            while (!stack.isEmpty() && Character.isDigit(stack.peek())) {
                sb.insert(0, stack.pop());
            }
            // StringBuild => String => Integer
            int count = Integer.valueOf(sb.toString());
            while (count > 0) {
                for (char ch : sub.toCharArray()) {
                    stack.push(ch);
                }
                count--;
            }
        }
    }
    // Convert all the letters in the stack into String
    StringBuilder retv = new StringBuilder();
    while (!stack.isEmpty()) {
        retv.insert(0, stack.pop());
    }
    return retv.toString();
}

The above is the international version of the praise code, which is really better understood than the official analysis of the Chinese website

q647 palindrome substring

Traverse from the middle to both sides to judge the qualified quantity. Both odd and even numbers should be considered

public int countSubstrings(String s) {
    int num = 0;
    int n = s.length();
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= 1; j++) {
            int l = i, r = i+j;
            while (l>=0 && r<=n-1 && s.charAt(l--) == s.charAt(r++)) {
                num++;
            }
        }

    }
    return num;
}

The sword finger t45 arranges the array into the smallest number

First, convert the number into a string array, and sort the string array using java's campareTo method and fast sorting

public String minNumber(int[] nums) {
    // First convert the nums array into a string array
    String[] strs = new String[nums.length];
    for (int i = 0; i < nums.length; i++) {
        strs[i] = String.valueOf(nums[i]);
    }
    quickSort(strs, 0, nums.length-1);
    // String splicing is not recommended. It needs to be copied again, which is slow
    StringBuilder res = new StringBuilder();
    for (String str : strs) {
        res.append(str);
    }
    return res.toString();
}

// Standard writing of fast row
private void quickSort(String[] strs, int low, int high) {
    if (low < high) {
        int middle = getMiddle(strs, low, high);
        quickSort(strs, low, middle - 1);
        quickSort(strs, middle + 1, high);
    }
}

private int getMiddle(String[] strs, int i, int j) {
    // Select the left boundary as the pivot
    String tmp = strs[i];
    while (i < j) {
        while (i < j && (strs[j] + tmp).compareTo(tmp + strs[j]) >= 0) j--;
        strs[i] = strs[j];
        while (i < j && (strs[i] + tmp).compareTo(tmp + strs[i]) <= 0) i++;
        strs[j] = strs[i];
    }
    strs[i] = tmp;
    return i;
}

5. Digital operation

q7 integer inversion (my weakness)

For some prior knowledge, the int of java type is 32 bits, and negative numbers can display one bit more than positive numbers. Interger.MAX_VALUE = 2147483647 is used

At each step, judge whether the size exceeds the limit. Do not save the middle as an array. Directly rev = rev * 10 + pop

If you can use long, it won't be so troublesome, because it won't overflow anyway. You can get the result and compare it with Interger.MAX_VALUE
q9 palindromes

Be proficient in the inversion code of numbers and understand all special situations

Special case: the last number is 0, odd or even, negative, and exceeds the maximum value of int during inversion

This question is half reversed
```
while (x>revertedNumber){
    int k = x % 10;
    revertedNumber = revertedNumber *10 + k;
    x /= 10;
}
```
The integral power of sword finger t16 value
1. The simple solution to the problem did not take into account many special situations
2. Considering special cases, exceptions are passed to global variables
3. Recursion, the 16th power can be regarded as the 8th power rediscovery
q31 next spread
1. Traverse from back to front to find the first non descending number i
2. Judge whether i > 0, otherwise execute 5 directly (i have an error in processing here)
3. Traverse from back to front to find the first number j greater than i
4. Swap i, j
5. Number after inverting i+1
6. Code optimization
```
while (i>=0){
    if(nums[i+1] > nums[i]){
        break;
    }
    i--;
}
// Can be optimized to
while (i>=0 && nums[i] >= nums[i + 1]){
            i--;
        }
```

q33 search rotation sort array

To make the event complexity O(log n), use binary search. Half of the binary search is ordered. Pay attention to the boundary problem

code:

public int search(int[] nums, int target) {
    int n = nums.length;
    int l = 0, r = n - 1;
    if(n == 0){
        return -1;
    }
    if(n == 1){
        return nums[0]==target?0:-1;
    }
    // Note the boundary conditions, when less than, when less than or equal to
    while (l <= r){
        int mid = (l+r)/2;
        if(nums[mid] == target){
            return mid;
        }
        // If the left is sequential; You must add equal to because in the case of only two numbers, 0==mid
        if(nums[0]<=nums[mid]){
            // This is left closed and right open
            if(nums[l]<=target && target<nums[mid]){
                r = mid-1;
            }
            else {
                l = mid+1;
            }
        }
        // If the right side is sequential, check from the right side
        else {
            if(nums[mid]<target && target<=nums[n-1]){
                l = mid+1;
            }
            else {
                r = mid-1;
            }
        }
    }
    return -1;
}

Summary:

For the middle number, the subscript is generally (length-1)/2. In the case of even numbers, it is customary to lose some in the first half. However, if only the left and right are divided, the middle number will be divided to the left
The left and right pointer loop exit conditions are left < = right
Pay attention to when it is less than or equal to, and you can't let go of any situation

q34 finds the first and last positions of elements in a sorted array

The same dichotomy is used to find the subscript of the first element greater than target with the adapted dichotomy

int leftIdx = binarySearch(nums, target-1);
int rightIdx = binarySearch(nums, target)-1;

// Binary search to find the first numeric subscript greater than target
public int binarySearch(int[] nums, int target){
    int left = 0, right = nums.length -1, ans = nums.length;
    while (left <= right){
        int mid = (left+right)/2;
        // Why is there no equal to? Because it is greater than, it is put in the else below
        if(nums[mid]>target){
            right = mid-1;
            ans = mid;
        } else {
            left = mid + 1;
        }
    }
    return ans;
}

q48 rotate image

Rotation in place is required. Temporary array cannot be returned

The simplest way is to overwrite the original array with the temporary array, but it's certainly not good

The best solution is to rotate the horizontal axis first, and then the main diagonal (don't rotate all one side in the process, so the value won't change)
q75 color classification

It is a special case of fast platoon to get the result in place and again. 1 is the middle number. If there is no requirement to traverse only once, directly find 1 as the sentry first.

Summary write quick sort: select a flag. After each traversal, the smaller one is on its left, the larger one is on its right, and the flag is in its final position. Divide and conquer left and right recursively to get the result
1. The concept of loop invariants, find the loop invariants of this problem, and it is best to write notes
```
//all in [p0,i) = 0
//all in [i,p2) = 1
//all in [p2,len-1] = 2
```
2. A single pointer needs to be traversed twice, and a double pointer can only be traversed once
```
while (i <= p2) {
    if (nums[i] == 0) {
        //The exchange cannot be 0
        swap(nums, i++, p0);
        p0++;
    } else if (nums[i] == 1) {
        //1 don't worry
        i++;
    } else if (nums[i] == 2) {
        //The exchange may be 2, so i can't add one
        swap(nums, i, p2);
        p2--;
    }
}
```

q128 longest continuous sequence

Linear time complexity required

You must first put the original array into the hashset and arrange the duplication by the way
Judge from the beginning. When you get each bit, you should constantly go to the one bit larger than it until the end to traverse whether it exists. If it exists, add one to the number
Because inner traversal is still O(n ²)， Therefore, it is necessary to judge in the middle of the outer traversal. Only the smaller bit of the current number exists can enter the inner traversal

public int longestConsecutive(int[] nums) {
    // Save to hashset
    Set<Integer> num_set = new HashSet<>();
    for (int num : nums) {
        num_set.add(num);
    }
    int longestStreak = 0;
    for (int num : num_set) {
        if (!num_set.contains(num-1)) {
            int currentStreak = num;
            int currentNum = 1;

            while (num_set.contains(currentStreak + 1)) {
                currentStreak+=1;
                currentNum+=1;
            }
            longestStreak = Math.max(currentNum, longestStreak);
        }
    }
    return longestStreak;
}

q169 most elements
1. Hash table save times
2. Sort first, and the last median element is the result
3. Randomize, randomly select a number in the middle each time, and traverse whether the count occupies more than half of the length
4. Divide and conquer, seek the mode from the top to the bottom
5. Voting algorithm, a little impression before. It can be proved
  
  Voting algorithm proof:
  1. If the candidate is not a maj, maj will oppose the candidate together with other non candidates, so the candidate will step down (a general election occurs when maj==0)
  2. If the candidate is a maj, maj will support himself and other candidates will oppose him. Similarly, maj will be elected successfully because maj has more than half of the votes
  nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
  candidate: 7 7 7 7 7 7 5 5 5 5 5 5 7 7 7 7
  count: 1 2 1 2 1 0 1 0 1 2 1 0 1 2 3 4
```
if (nums[i] == candidate) {
    count++;
} else {
    count--;
    if (count < 0) {
        candidate = nums[i];
        count = 1;
    }
}
```
  The optimization code is
```
if (count == 0) {
    candidate = nums[i];
}
count += nums[i] == candidate ? 1 : -1;
```

6. Array operation

q238 product of arrays other than itself

It is required that division cannot be used, and it should be completed in O(n), with the lowest spatial complexity

Define two arrays, one is the product of all numbers on the left of the current index, and the other is the product of all numbers on the right. The endpoint value is 1. The result array is the multiplication of the two arrays

The second array can operate at the position of the first array
```
public int[] productExceptSelf(int[] nums) {
    int len = nums.length;
    if (len == 0) {
        return null;
    }
    int res[] = new int[len];
    res[0] = 1;
    for (int i = 1; i < len; i++) {
        res[i] = res[i-1] * nums[i-1];
    }
    int R = 1;
    for (int i = len - 1; i >= 0; i--) {
        res[i] = res[i] * R;
        R *= nums[i];
    }
    return res;
}
```
q240 search two-dimensional matrix
1. Use binary lookup for each row
  
  for (int[] row : matrix)
  
  The loop condition of binary search is while (left < = right)
2. Z igzag
  
  Starting from the upper right corner, the larger one moves to the left and the smaller one moves to the right
q4 find the median of two ordered arrays
1. analysis
  
  Sort first and then search in sequence. The event complexity is O(m+n). log(m+n) is required. Only two points can be used, one small half and one small half can be excluded
2. step
  1. If the median should be the smallest k (even number is the average of the middle two numbers), define a function to find the smallest k in the two arrays
  2. Compare the last sliding window sequence number in the two arrays, exclude the k/2 number of the smaller one each time, and refresh k
3. summary
  1. Pay attention to the boundary condition, k=1 or at the end of the sequence number, you can get the answer directly
  2. In the future, half of this exclusion is generally k/2-1, so as to ensure safety under the condition of excluding as many as possible
  3. The final answer is that int is calculated as double, and finally divided by 2.0
q56 merge interval

There are many things to learn about this problem
1. Two dimensional array sorting, using the method of overriding the Comparator interface
  - Common method
```
//First, sort the two-dimensional array according to the size of the left boundary
for (int i = 0; i < intervals.length-1; i++) {
    if(intervals[i][0]>intervals[i+1][0]){
        for (int j = 0; j < 2; j++) {
        }
    }
}
```
  - Good way
```
Arrays.sort(intervals, new Comparator<int[]>() {
    @Override
    public int compare(int[] o1, int[] o2) {
        return o1[0]-o2[0];
    }
});
```
    0 in brackets represents column 0, left minus right represents ascending order, and ordinary one-dimensional array sorting without brackets
2. Conversion between arrays and collections
  1. It's better to convert the array to the collection by a for loop and add one by one (if the asList method is an array, it must be a reference type)
  2. The. toArray method can be used to convert a collection to an array, with the parameters that need to be converted to (Object type without parameters)
    - If there is an array to connect, the size of arrays initialization is arbitrary. If it is directly converted internally, it must be initialized to list.size(), otherwise the array length will be extended and zero will be filled later. See the following source code for details
      public <T> T[] toArray(T[] a) { if (a.length < size) // Make a new array of a's runtime type, but my contents: return (T[]) Arrays.copyOf(elementData, size, a.getClass()); System.arraycopy(elementData, 0, a, 0, size); if (a.length > size) a[size] = null; return a; }
```
int[] nums = new int[3];
        List<Integer> list = new ArrayList<Integer>(){};
        list.add(1);
        list.add(2);
        list.add(3);

//        Integer[] arrays = new Integer[0];
//        Integer[] we = list.toArray(arrays);
//        System.out.println(we[2]);

        Integer[] arrays = new Integer[list.size()];
        list.toArray(arrays);
        System.out.println(arrays[3]);
```
  - Object [] cannot be converted to String []. To convert, you can only take out each element and convert it again. The forced type conversion in java is only for a single object. You can't be lazy to convert the whole array into another type of array, which is similar to the need to initialize the array one by one.
q283 move zero

I can't do simple questions, that is, double pointers. Both pointers start from the 0 position. The right pointer is responsible for finding non-zero numbers, and the left pointer is responsible for pointing to the last position in a fixed sequence
```
public void moveZeroes(int[] nums) {
    int i = 0, j = 0;
    while (j < nums.length) {
        if (nums[j] != 0) {
            swap(nums, i, j);
            i++;
        }
        j++;
    }
}
```
q287 finding duplicate arrays
1. My method is to create an array of the same length, traverse a value, and assign it as the value of the array index to 1. If I find the index value again, I find that it is not 0. But this is not a constant space
```
public int findDuplicate(int[] nums) {
    int n = nums.length;
    int[] ind = new int[n];
    for (int i = 0; i < n; i++) {
        if (ind[nums[i]-1] != 0) {
            return nums[i];
        }
        ind[nums[i]-1] = 1;
    }
    return 0;
}
```
2. Speed pointer
  
  Construct a graph for the nums array, and each position I is connected with an edge of I → nums[i]. Because there is a duplicate number target, the position of target must have at least two edges pointing to its value. Therefore, there must be a ring in the whole graph, and then use the previous ring linked list method to find the entry of the ring
3. dichotomy
  
  I don't quite understand for the moment. When it is an ordered array, take left = 1, right = len - 1 directly, and then calculate Mid. the result is equivalent to sorting and then calculating mid?

q347 top K high frequency elements, same type: Sword finger t40

Using hash + small top heap, hash thought of it. I don't know how to optimize with small top heap

PriorityQueue is a heap api in java. It traverses the number of occurrences of each number in the hash. If it is larger than the small top heap, it will be replaced

public int[] topKFrequent(int[] nums, int k) {
    // Store each element and its number of occurrences in the hash table
    Map<Integer, Integer> occurrences = new HashMap<Integer, Integer>();
    for (int num : nums) {
        occurrences.put(num, occurrences.getOrDefault(num, 0) + 1);
    }
    // Build small root heap
    PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() {
        @Override
        public int compare(int[] m, int[] n) {
            return m[1] - n[1];
        }
    });
    // Maintain heap values
    for (Map.Entry<Integer, Integer> entry : occurrences.entrySet()) {
        int num = entry.getKey(), count = entry.getValue();
        if (queue.size() == k) {
            if (count > queue.peek()[1]) {
                queue.poll();
                queue.offer(new int[]{num, count});
            }
        } else {
            queue.offer(new int[]{num, count});
        }
    }
    // Return result array
    int[] res = new int[k];
    for (int i = 0; i < k; i++) {
        res[i] = queue.poll()[0];
    }
    return res;
}

Based on the quick sort method, I'll look at it later. I understand the general meaning

q406 reconstruct the queue according to height

The installation shall be sorted from low to high first. If the height is the same, it shall be sorted according to the position from large to small, because the high always ignores the low. If the low is arranged first, it will not affect the "greater than or equal" position of the high. If the height is the same, the high "greater than or equal" value shall be arranged first, which will not affect the small value. Otherwise, it is troublesome to judge the size every time

Determine the position in the two-dimensional array according to the spaces value and person[1] value

public int[][] reconstructQueue(int[][] people) {
    // Sort first
    Arrays.sort(people, (person1, person2) -> {
        // If the two are the same, first determine the latter, and the front will not be affected
        if (person1[0] == person2[0]) {
            return person2[1] - person1[1];
        } else {
            return person1[0] - person2[0];
        }
    });
    // Application array
    int n = people.length;
    int[][] res = new int[n][];
    for (int[] person : people) {
        int spaces = person[1] + 1;
        for (int i = 0; i < n; i++) {
            if (res[i] == null) {
                spaces--;
            }
            if (spaces == 0) {
                res[i] = person;
                break;
            }
        }
    }
    return res;
}

q448 find all missing numbers in the array

Since the request needs to be in place, you can only use the original array. Finally, see whether the request needs to be restored

Learn this idea. Traverse the array, take each value as a subscript, and add n after finding the position. After that, the number subscript that does not disappear exceeds n, and the subscript that does not exceed is the answer. Note that the subscript calculation is: int x = (Num [i] - 1)% n;

q494 objectives and

Violent backtracking, the positive and negative of each element

  int count = 0;
    
  public int findTargetSumWays(int[] nums, int target) {
      // Violent backtracking
      dfs(nums, target, 0, 0);
      return count;
  }

  private void dfs(int[] nums, int target, int index, int sum) {
    if (index == nums.length) {
        if (sum == target) {
            count++;
        }
    } else {
        dfs(nums, target, index+1, sum - nums[index]);
        dfs(nums, target, index+1, sum + nums[index]);
    }
  }

Into knapsack problem

The sum of the elements added with the - sign is neg = > (sum − neg) − neg=sum − 2 ⋅ neg=target

neg=(sum−target)/2

The value in the behavior array is listed as a combined number, up to neg

Boundary condition: dp[0] [0] = 1

My three questions are shown in the following notes

public int findTargetSumWays(int[] nums, int target) {
    int sum = 0;
    for (int i = 0; i < nums.length; i++) {
        sum += nums[i];
    }
    int dif = sum - target;
    // 1. Forget to add this judgment
    if (dif < 0 || dif % 2 == 1){
        return 0;
    }
    int neg = dif / 2;
    int[][] dp = new int[nums.length + 1][neg + 1];
    // boundary condition 
    dp[0][0] = 1;
    for (int i = 1; i <= nums.length; i++) {
        for (int j = 0; j <= neg; j++) {
        	// 2. Ignored - 1
            if (nums[i-1] > j) {
                // 3. I don't remember+=
                dp[i][j] += dp[i-1][j];
            } else {
                dp[i][j] += dp[i-1][j] + dp[i-1][j-nums[i-1]];
            }
        }
    }
    return dp[nums.length][neg];
}

Optimized to a one-dimensional array

// boundary condition 
dp[0] = 1;
for (int num : nums) {
	// Traverse from back to front, because the later ones need to use the previous calculation to prevent the previous ones from changing first
	// Yes > = num, not > 0
    for (int j = neg; j >= num; j--) {
        dp[j] += dp[j-num];
    }
}
return dp[neg];

q581 shortest unordered continuous subarray
1. First sort the array, and then compare which places in the middle to sort
2. Double pointer
  
  Find left from right to left, update min if it is less than min, mark it as left if it is greater than min, and the last left is the real left. Find right. The same is true
3. It is divided into three parts

q739 daily temperature

Violence, see note for details

public int[] dailyTemperatures(int[] temperatures) {
    // next []: the subscript for the first occurrence of each temperature. The subscript represents the temperature, and the value represents the subscript for the first occurrence
    // index: higher than its temperature and the nearest subscript;
    int n = temperatures.length;
    int[] next = new int[101];
    int[] ans = new int[n];
    Arrays.fill(next, Integer.MAX_VALUE);
    // Traverse from back to front
    for (int i = n - 1; i >= 0; i--) {
        // Find the first element after it in the next that is larger than it, such as temperatures[i] == 76 °, and find it from 77 °
        // Find everything bigger than him, and then find the one closest to it
        int index = Integer.MAX_VALUE;
        for (int j = temperatures[i] + 1; j < 101; j++) {
            if (next[j] < index) {
                index = next[j];
            }
        }
        // I forgot to add this before. If there is no higher temperature than that later
        if (index < Integer.MAX_VALUE) {
            ans[i] = index - i;
        }
        next[temperatures[i]] = i;
    }
    return ans;
}

Monotone stack: ensure that the number in the stack decreases monotonically. If the element to be put into the stack is larger than the element at the top of the stack, then all the elements smaller than him are out of the stack, and calculate the distance to get the result

public int[] dailyTemperatures(int[] temperatures) {

    int n = temperatures.length;
    int[] ans = new int[n];
    Deque<Integer> stack = new LinkedList<>();
    for (int i = 0; i < n; i++) {
        // Compare the size of the traversed element and the top element of the stack
        while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
            int pop = stack.pop();
            ans[pop] = i - pop;
        }
        stack.push(i);
    }
    return ans;
}

The minimum value of sword finger t11 rotation array. See notes for details

public int minArray(int[] numbers) {
    int left = 0, right = numbers.length - 1;
    while (left < right) {
        // In this way, the midpoint will not overflow
        int mid = left + (right - left) / 2;
        if (numbers[mid] < numbers[right]) {
            right = mid;
        } else if (numbers[mid] > numbers[right]){
            // This mid cannot be the minimum value, so it can be excluded
            left = mid + 1;
        } else {
            // mid and right are the same, and one right can be excluded
            right--;
        }
    }
    return numbers[left];
}

7. Tree operation

Substructure of sword finger t27 tree
1. Recursively traverse the main tree to find nodes with the same root node value
2. If the root node is the same, start to enter whether the two trees are the same recursive traversal

q98 validate binary search tree

ergodic

public boolean isValidBST(TreeNode node, long lower, long upper){
        if(node == null){
            return true;
        }
        if(node.val <= lower || node.val >= upper){
            return false;
        }
        return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);
}

Why use long? Because the maximum value of a single node in the test case is the maximum value of lnt type

Medium order traversal

The middle order traversal of binary search tree is incremental. If you want to reduce the time complexity, use stack

To judge whether the collection is empty, you cannot use = = null, but. isEmpty or. size == 0

public boolean isValidBST(TreeNode root) {
    Deque<TreeNode> stack = new LinkedList<TreeNode>();
    long inorder = Long.MIN_VALUE;

    while (!stack.isEmpty() || root != null){
        while (root != null){
            stack.push(root);
            root = root.left;
        }
        root = stack.pop();
        if(root.val <= inorder){
            return false;
        }
        inorder = root.val;
        root = root.right;
    }
    return true;
}

q101 symmetric binary tree

I use the traversal order of the left and right roots and the right and left roots, and then compare the values. This is a typical error. The same result may be asymmetric trees, such as 1, 2 and 3 with only left subtrees

The first method is recursion, going left and back

public boolean isSymmetric(TreeNode root) {
    if(root == null) {
        return true;
    }
    return helper(root.left, root.right);
}

public boolean helper(TreeNode p, TreeNode q) {
    if(p == null && q == null) {
        return true;
    }
    if(p == null || q == null) {
        return false;
    }
    //If one of them is false, it is false. If all of them are true, it is true
    return p.val == q.val && helper(p.left, q.right) && helper(p.right, q.left);
}

If all the values passed into the helper for the first time are root, the comparison times will be doubled

The second method is to iterate, using queue comparison. The left side enters the team and the right side enters the team, and the two are the same continuously

public boolean check(TreeNode u, TreeNode v) {
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(u);
        q.offer(v);
        while (!q.isEmpty()) {
            u = q.poll();
            v = q.poll();
            if (u == null && v == null) {
                continue;
            }
            if ((u == null || v == null) || (u.val != v.val)) {
                return false;
            }

            q.offer(u.left);
            q.offer(v.right);

            q.offer(u.right);
            q.offer(v.left);
        }
        return true;
}

If it's not recursion, then true and false are a hammer deal

Hierarchical traversal of q102 binary tree

The main purpose of using a queue is to find out which layer it belongs to. Otherwise, record each node and its level when transmitting values. In fact, you can also calculate the number of nodes in the current layer before you go out of the queue and join the children in the queue. After understanding this, you can write it without looking at the official code

A good way to write code: don't try to be perfect at the beginning. You can write it in sequence without adding a loop, and then add a loop according to the loop logic. The while loop here is added later

Two things have been changed through test cases
1. In the left and right stages, you can't join the team until you judge that it can't be empty
2. Judge whether the root node is empty before joining the queue
```
public List<List<Integer>> levelOrder(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> list = new ArrayList<>();

    if (root == null){
        return res;
    }
    queue.offer(root);
    while (!queue.isEmpty()) {
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode p = queue.poll();
            list.add(p.val);
            if (p.left != null) {
                queue.offer(p.left);
            }
            if (p.right != null) {
                queue.offer(p.right);
            }
        }
        res.add(new ArrayList<>(list));
        list.clear();
    }
    return res;
}
```
You can optimize it again. List = new ArrayList < > (); Change to the beginning of the while loop, so only res.add(list) is used; You don't need clear

Depth of binary tree

At the beginning, I wrote a preorder traversal, but I don't remember the deepest record, g

It records the deepest layer, but the basic type of java is value transfer, which will not affect the basic type value of the main function. A global Max must be defined. this.max, g when transferring the value

int max = 0;
    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int depth = 0;
        preOrder(root, depth, max);
        return max;
    }

    public void preOrder(TreeNode node, int depth, int max) {
        depth++;
        if (node != null){
            if(depth>max){
                this.max = depth;
            }
            preOrder(node.left, depth, this.max);
//            depth--; Don't add this! Basic type, recursion will not change itself!!!
            preOrder(node.right, depth, this.max);
//            depth--;
        }
    }

For this basic type of design problem, it is best to set the return value when defining the dfs function

public int maxDepth(TreeNode root) {
    return getDepth(root, 0);
}

public int getDepth(TreeNode node, int depth) {
    if(node == null){
        return depth;
    }
    return Math.max(getDepth(node.left, depth+1), getDepth(node.right, depth+1));
}

Official explanation

public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
   }

You can also use hierarchy traversal to return the last number of layers

q105 construct binary tree from preorder and inorder traversal sequences

I can only analyze, draw pictures by hand, and write code

Look at the problem solution. You can use recursion

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-w0tk8jsz-163771461965 9) (C: / users / chenzhijian / appdata / roaming / typora / typera user images / image-20211021200146164. PNG)]

When building a binary tree (you can think about similar problems in this way), think macroscopically. First get the root node, and then recursively get the left node and right node of the root node. The interval of the recursive function continues to narrow until it is as small as one, get the root node (leaf node) of the deepest stack, or even go too far. Return null and start to exit the recursive stack
```
public TreeNode buildTree(int[] preorder, int[] inorder) {
    int n = inorder.length;
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < n; i++) {
        map.put(inorder[i], i);
    }

    return myBuildTree(preorder, 0, n-1, map, 0, n-1);
}

private TreeNode myBuildTree(int[] preorder, int preLeft, int preRight,
                        Map<Integer, Integer> map, int inLeft, int inRight) {
    if(preLeft > preRight || inLeft > inRight){
        return null;
    }
    int rootVal = preorder[preLeft];
    TreeNode root = new TreeNode(rootVal);
    int pIndex = map.get(rootVal);

    root.left = myBuildTree(preorder, preLeft+1, pIndex-inLeft+preLeft,
                            map, inLeft, pIndex-1);
    root.right = myBuildTree(preorder, pIndex-inLeft+preLeft+1, preRight,
                            map, pIndex+1, inRight);
    return root;
}
```
Here, the root node value found in the preorder traversal sequence is used to find the index corresponding to the inorder traversal sequence. The hash table is used for space for time
q114 binary tree expanded into linked list
1. Learn the iterative writing method of preorder traversal first
  
  The preorder traversal of binary tree iterates to realize root left right
  
  Idea:
  1. Borrowing stack structure
  2. First push(root)
  3, node = pop()
  3.1,list.add( node.val )
  3.1,push( node.right )
  3.3,push( node.left )
  4. Loop step 3 until the stack is empty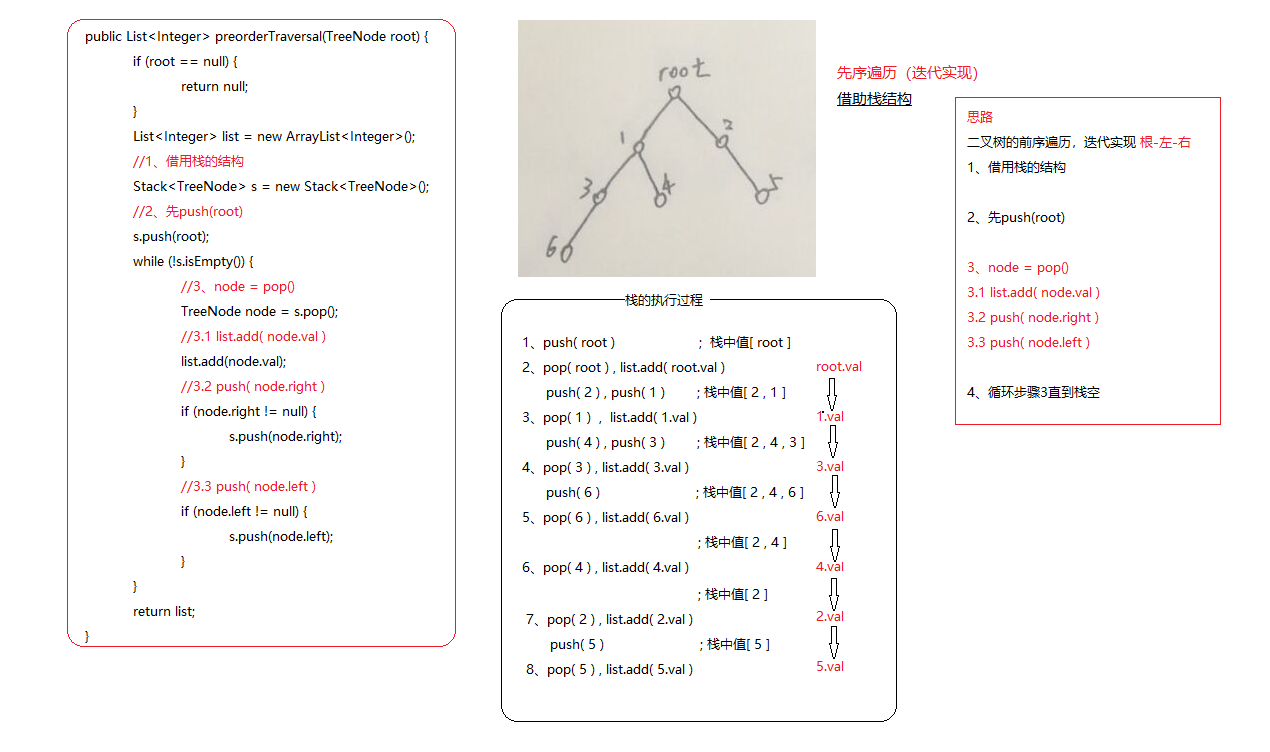
2. Use the first order traversal, store the nodes in the traversal order into the List, and then create a new linked List according to the original root directory address, because treenode newroot = root; The address pointed to by newroot is also the address pointed to by root, so it can also be regarded as in place. java print pointer is generally the address pointed to by the output pointer

q208 implements prefix tree

Code Trie[] children = new Trie[26]; It means to create 26 child nodes of the same type for the Trie node, and the next child node is node.children[i]

Now let's learn how to define a class

class Trie {

      private Trie[] children;
      private boolean isEnd;

    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }

    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            char c = word.charAt(i);
            int index = c - 'a';
            if (node.children[index] == null) {
                node.children[index] = new Trie();
            }
            node = node.children[index];
        }
        node.isEnd = true;
    }

    public boolean search(String word) {
        Trie node = searchPrefix(word);
        return node != null && node.isEnd;
    }

    public boolean startsWith(String prefix) {
        return searchPrefix(prefix) != null;
    }

    private Trie searchPrefix(String prefix) {
        Trie node = this;
        for (int i = 0; i < prefix.length(); i++) {
            char c = prefix.charAt(i);
            int index = c - 'a';
            if (node.children[index] == null) {
                return null;
            }
            node = node.children[index];
        }
        return node;
    }
}

236 nearest common ancestor of binary tree

Find the recursive exit, find the return node, and return null if not found
Left's left child found, return is also left
After this round of recursion, judge that if left does not exist, right will be returned to TreeNode right, and if right does not exist, left will be returned

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null) {
        return null;
    }
    if (root == p || root == q) {
        return root;
    }
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p ,q);
    if (left == null) {
        return right;
    }
    if (right == null) {
        return left;
    }
    return root;
}

q337 house raiding III

We can use f(o) to represent the maximum weight sum of the selected node on the subtree of O node when O node is selected; g(o) represents the maximum weight sum of the selected node on the subtree of the O node without selecting the O node; l and r represent the left and right children of O.

When o is selected, the left and right children of O cannot be selected, so the sum of the maximum weights of the selected points on the subtree when o is selected is the sum of the maximum weights of l and r that are not selected, that is, f(o) = g(l) + g ®
When o is not selected, the left and right children of O can be selected or not selected. For a specific child X of O, its contribution to o is the larger value of the sum of weights when x is selected and not selected. So g(o) =max{f(l),g(l)}+max{f ®, g ®}

Why use follow-up traversal, because you must first determine the son before you can determine whether the father chooses or not
1. Use a hash table to store the maximum value corresponding to the tree node
```
public int rob(TreeNode root) {
    Map<TreeNode, Integer> f = new HashMap<TreeNode, Integer>();
    Map<TreeNode, Integer> g = new HashMap<TreeNode, Integer>();

    dfs(root, f, g);
    return Math.max(f.getOrDefault(root, 0), g.getOrDefault(root, 0));
}

private void dfs(TreeNode node, Map<TreeNode, Integer> f, Map<TreeNode, Integer> g) {
    if (node != null) {
        dfs(node.left, f, g);
        dfs(node.right, f, g);
        f.put(node, node.val + g.getOrDefault(node.left, 0) + g.getOrDefault(node.right, 0));
        g.put(node, Math.max(f.getOrDefault(node.left, 0), g.getOrDefault(node.left, 0)) + Math.max(f.getOrDefault(node.right, 0), g.getOrDefault(node.right, 0)));
    }
}
```
2. Omit the hash array, and only use two arrays with length of 2 to represent the left and right respectively, 0 means to select and 1 means not to select
```
public int rob(TreeNode root) {
    int[] res = dfs(root);
    return Math.max(res[0], res[1]);
}

private int[] dfs(TreeNode node) {
    if (node != null) {
        int[] l = dfs(node.left);
        int[] r = dfs(node.right);
        int selected = node.val + l[1] + r[1];
        int notSelected = Math.max(l[0], l[1]) + Math.max(r[0], r[1]);
        return new int[]{selected, notSelected};
    } else {
        return new int[]{0, 0};
    }
}
```

q437 path sum III

Violence law, one dfs at each location, dfs set of dfs

Prefix, I don't understand. Keep reading

/**
 * ---Analysis of algorithm ideas
 *The number of paths that meet the requirements. Obviously, all paths need to be considered (traversing the tree)
 * Traverse the tree in depth, and find the sum cur of the path node values from the root to the current node for each node visited; (that is, the prefix sum of the node, and the node prefix sum includes itself)
 * At this time, HashMap has recorded the prefix sum of all nodes before the node (HashMap < prefix sum, quantity >)
 * By searching cur targetsum, you can know the number of solutions that end at the current node path; (in the process of traversing the tree, count the number of solutions that end at each access node, so as to obtain all solutions.)
 * HahsMap.put(cur ，HashMap.get(Current prefix and) + 1)
 * HashMap Pop up occurs when the current node recursively returns
 * ---Algorithm structure design
 *
 * For each node
 *      When traversing down, update the HashMap first
 *      Update (restore) HashMap on recursive return
 *      Solve the current node solution

 * */

public class SoPathSum {
    int res=0;
    Map<Integer,Integer> map = new HashMap<>();
    public int pathSum(TreeNode root,int targetSum){
        map.put(0,1);//Each node's own value = targetSum
       traverse(root,0,targetSum);

        return res;

    }
    private void traverse(TreeNode node,int cur,int targetSum){
        if(node == null){
            return ;
        }
        cur+=node.val;
        map.put(cur,map.getOrDefault(cur,0)+1);
        traverse(node.left,cur,targetSum);
        traverse(node.right,cur,targetSum);
        map.put(cur,map.get(cur)-1);

        //Process current node
        res+= map.getOrDefault(cur-targetSum,0);

    }
}

q538 transforms binary search tree into cumulative tree

It is reverse middle order traversal. The original return value can also be used as no return value

That's OK

class Solution {
	// In fact, it is more recommended not to define global traversal and define a recursive function to follow
    int sum = 0;

    public TreeNode convertBST(TreeNode root) {
        if (root != null) {
            convertBST(root.right);
        	sum += root.val;
        	root.val = sum;
        	convertBST(root.left);
        }
    }
}

Diameter of q543 binary tree

By recursively calculating the depth, the answer = max (left subtree depth, right subtree depth). The answer does not enter the recursion stack, but only uses the recursive process data

int ans = 0;

public int diameterOfBinaryTree(TreeNode root) {
    depth(root);
    return ans;
}

private int depth(TreeNode node) {
    if (node == null) {
        return 0;
    }
    int L = depth(node.left);
    int R = depth(node.right);
    ans = Math.max(ans, L + R);
    return Math.max(L, R) + 1;
}

q617 merge binary tree

Simple dfs with return value still can't write and can only be understood

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
    if (root1 == null) {
        return root2;
    }
    if (root2 == null) {
        return root1;
    }

    TreeNode root = new TreeNode(root1.val + root2.val);
    root.left = mergeTrees(root1.left, root2.left);
    root.right = mergeTrees(root1.right, root2.right);

    return root;
}

Substructure of sword finger t26 tree

For two dfs, first find the same bytes as the root node of the sub tree on the main tree, and then start the dfs comparison

If the left subtree of a and the left subtree of b are empty at the same node, it is proved that the left subtree is ok, otherwise it is reverse

public boolean isSubStructure(TreeNode A, TreeNode B) {
    // Traverse the node of A until it is the same as the root node of B
    // This result is very useful in many recursions whose return value is bool type. It is applicable to success with a successful result
    boolean result = false;
    if (A != null && B != null) {
        if (A.val == B.val) result = reCur(A, B);
        if (!result) result = isSubStructure(A.left, B); // Give me another chance
        if (!result) result = isSubStructure(A.right, B); // Keep giving it a chance. There's an achievement anyway
    }
    return result;
}

private boolean reCur(TreeNode a, TreeNode b) {
    if (b == null) return true;
    if (a == null) return false;
    if (a.val != b.val) return false;
    return reCur(a.left, b.left) && reCur(a.right, b.right);
}

Mirror image of sword finger t27 binary tree

public TreeNode mirrorTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        // My method is also OK
//        TreeNode node = root.left;
//        root.left = root.right;
//        root.right = node;
//        mirrorTree(root.left);
//        mirrorTree(root.right);
		// This can be used as a template for binary tree recursion with return value
        TreeNode left = mirrorTree(root.left);
        TreeNode right = mirrorTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }

Sword finger t28 symmetric binary tree

I wrote it myself, but it's not beautiful enough. The annotation is the standard answer

In the future, the topic of simultaneous comparison of binary trees is that two parameters are recursive at the same time

public boolean isSymmetric(TreeNode root) {
		// return root == null ? true : recur(root.left, root.right);
        return isSymmetric(root, root);
    }

    private boolean isSymmetric(TreeNode root1, TreeNode root2) {
        if (root1 == null && root2 != null) return false;
        if (root1 != null && root2 == null) return false;
        if (root1 == null && root2 == null) return true;
        if (root1.val != root2.val) return false;
//        if (root1 == null && root2 == null) return true;
//        if (root1 == null || root2 == null || root1.val != root2.val) return false;
        return isSymmetric(root1.left, root2.right) && isSymmetric(root1.right, root2.left);
    }

8. Operation diagram

q200 number of islands

Using dfs, it is set to '0' after each traversal

The height and width can not follow the recursive function, because they can be obtained every time. Whether the traversed position is in the graph can be determined after recursion, rather than before each recursion

public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }
        int h = grid.length;
        int l = grid[0].length;
        int num_islands = 0;

        for (int i = 0; i < h; i++) {
            for (int j = 0; j < l; j++) {
                if (grid[i][j] == '1') {
                    num_islands++;
                    dfs(grid, i, j);
                }
            }
        }

        return num_islands;
    }

    private void dfs(char[][] grid, int i, int j) {
        // Lower right and upper left to judge whether it is within the boundary
        int h = grid.length;
        int l = grid[0].length;

        if (i >= 0 && i < h && j >= 0 && j < l && grid[i][j] != '0') {
            grid[i][j] = '0';
            dfs(grid, i, j + 1);
            dfs(grid, i + 1, j);
            dfs(grid, i, j - 1);
            dfs(grid, i - 1, j);
        }
    }

Using bfs is the same as dfs except that the traversal method is different

Deque for stack and Quere for team are LinkedList

Since the traversal here is a two-dimensional array, the first node must be traversed once at the beginning of each position, so the double for loop first enters the queue. Then, if the queue is not empty, go out of the queue every time to judge whether there is a nearby node with '1'. If there is, enter the queue. The node added here is a one-dimensional value of the two-dimensional array, which can be restored to two-dimensional coordinates

for (int i = 0; i < h; i++) {
    for (int j = 0; j < l; j++) {
        if (grid[i][j] == '1') {
            num_islands++;
            grid[i][j] = '0';
            Queue<Integer> queue = new LinkedList<>();
            queue.add(i * l + j);
            while (!queue.isEmpty()) {
                int id = queue.remove();
                int row = id / l;
                int col = id % l;
                if (row - 1 >= 0 && grid[row-1][col] == '1') {
                    grid[row-1][col] = '0';
                    queue.add((row-1)*l+col);
                }
                if (row + 1 < h && grid[row+1][col] == '1') {
                    grid[row+1][col] = '0';
                    queue.add((row+1)*l+col);
                }
                if (col - 1 >= 0 && grid[row][col-1] == '1') {
                    grid[row][col-1] = '0';
                    queue.add(row * l + col - 1);
                }
                if (col + 1 < l && grid[row][col+1] == '1') {
                    grid[row][col+1] = '0';
                    queue.add(row * l + col + 1);
                }
            }
        }
    }
}

q207 Curriculum

The same can be done using two recursive methods

At the beginning, my thinking was limited. I thought it was too complicated to operate through two-dimensional array. In fact, I transformed it into a graph according to two-dimensional array, and then solved the problem further. The result is whether the directed graph has a ring (whether it is a topological graph or not)

Thinking:
1. The basic data type cannot change with the change of the function, so the bool value is directly regarded as a global traversal and cannot change with recursion
2. In fact, courses are incremented continuously by default, so edges.get(item[1]).add(item[0]) just uses numCourses space
3. There are three states: 0 has not been accessed, 1 is being accessed, and access completion = = 2 (as long as it is not 01)
```
boolean valid = true;

public boolean canFinish(int numCourses, int[][] prerequisites) {
    List<List<Integer>> edges = new ArrayList<>();
    int[] visited = new int[numCourses];
    for (int i = 0; i < numCourses; i++) {
        edges.add(new ArrayList<>());
    }
    for (int[] item : prerequisites) {
        edges.get(item[1]).add(item[0]);
    }
    for (int i = 0; i < numCourses && valid; i++) {
        if (visited[i] == 0) {
            dfs(edges, visited, i);
        }
    }
    return valid;
}

public void dfs(List<List<Integer>> edges, int[] visited, int i) {
    visited[i] = 1;
    List<Integer> list = edges.get(i);
    for (int u : list) {
        if (visited[u] == 0) {
            dfs(edges, visited, u);
            // The following three lines are not added. They are added faster
            if(!valid) {
                return;
            }
        }
        if (visited[u] == 1) {
            valid = false;
            return;
        }
    }
    visited[i] = 2;
}
```
bfs method, forward thinking, first find the node with access degree of 0, remove it, and then remove the node with access degree of 0 every time. Finally, if there is no node, it is proved to be a topology graph

In the code

Use a queue for breadth first search. Initially, all nodes with a degree of 0 are put into the queue. They are the top nodes that can be sorted as topology, and the relative order between them is irrelevant.

In each step of breadth first search, we take out the first node uu:

We put uu in the answer;

We remove all out edges of uu, that is, reduce the penetration of all adjacent nodes of uu by 1. If the penetration of an adjacent node v becomes 0, we put v in the queue.

At the end of the breadth first search process. If the answer contains these n nodes, then we find a topological sort. Otherwise, it means that there are rings in the graph, and there is no topological sort.

q79 word search

Since it is not required to find the path, as long as the result, dfs is best defined as a function with a return value of bool type
If no result is found, the points at all positions should be traversed as the starting point. In the process of traversing the previous starting point, if it gets false, it will not be processed. If one of them is true, there will be a solution
The problem solution defines a function for calculating the orientation. If you go in more directions, you'd better use the orientation function. My idea is to judge which side to go from

int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

for (int[] dir : directions) {
int newi = i + dir[0], newj = j + dir[1];
if (newi >= 0 && newi < board.length && newj >= 0 && newj < board[0].length)
Be sure to use [i][j] = false before leaving;

When the return value of a recursive function is bool type, this method is used when you want to return false and return true successfully

if(dfs(board, chars, used, ni, nj, k+1)) return true;

public boolean exist(char[][] board, String word) {
    int m = board.length;
    if(m == 0){
        return false;
    }
    int n = board[0].length;
    //Mark whether to walk
    boolean[][] used = new boolean[m][n];
    char[] chars = word.toCharArray();
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if(dfs(board, chars, used, i, j, 0)){
                return true;
            }
        }
    }
    return false;
}

public boolean dfs(char[][] board, char[] chars, boolean[][] used, int i, int j, int k){
        //Top right and left x
        if(k == chars.length-1){
            return board[i][j] == chars[k];
        }
        if (board[i][j] == chars[k]){
            int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
            used[i][j] = true;
            for (int[] direction : directions) {
                int ni = i + direction[0];
                int nj = j + direction[1];
                //Judge whether it is still in the matrix area and the next area has not been accessed
                if(ni >= 0 && ni < board.length && nj >= 0 && nj < board[0].length && used[ni][nj] == false){
                    if(dfs(board, chars, used, ni, nj, k+1)){
                        return true;
                    }
                }
            }
            used[i][j] = false;
        }
        return false;
}

Motion range of sword finger t13 robot

dfs without return value, I wrote it

int count = 0;

public int movingCount(int m, int n, int k) {
    // dfs, judge whether it is out of bounds and whether the digit sum exceeds k each time
    // If the location has been accessed, the result is + 1, and it will no longer be restored to not accessed

    // Do it with bfs
    boolean[][] vis = new boolean[m][n];
    bfs(m, n, 0, 0, k, vis);
    return count;
}

  private void bfs(int m, int n, int i, int j, int k, boolean[][] vis) {
  	// Do not remember to write vis[i][j] == false condition, resulting in timeout
    if (i < m && j < n && (singleSum(i) + singleSum(j)) <= k && vis[i][j] == false) {
        count++;
        vis[i][j] = true;
        bfs(m, n, i+1, j, k ,vis);
        bfs(m, n, i, j+1, k ,vis);
    }
  }

  private int singleSum(int i) {
    int sum = 0;
    while (i != 0) {
        sum += i % 10;
        i /= 10;
    }
    return sum;
  }

dfs with return value, written by Tsinghua boss

public int movingCount(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        return dfs(0, 0, m, n, k, visited);
    }
    public int dfs(int i, int j, int m, int n, int k, boolean[][] visited) {
        if(i >= m || j >= n || k < getSum(i) + getSum(j) || visited[i][j]) {
            return 0;
        }
        visited[i][j] = true;
        return 1 + dfs(i + 1, j, m, n, k, visited) + dfs(i, j + 1, m, n, k, visited);
    }

bfs, similar to the hierarchical traversal of a tree

public int movingCount(int m, int n, int k) {
    int count = 0;
    boolean[][] vis = new boolean[m][n];
    int[][] directions = new int[][]{{0, 1}, {1, 0}};
    Queue<int[]> queue = new LinkedList<>();
    queue.offer(new int[]{0, 0});
    vis[0][0] = true;
    count++;
    while (!queue.isEmpty()) {
        int[] poll = queue.poll();
        int i = poll[0];
        int j = poll[1];
        for (int[] direction : directions) {
            int ni = i + direction[0];
            int nj = j + direction[1];
            if (ni < m && nj < n && !vis[ni][nj] && (singleSum(ni) + singleSum(nj) <= k)) {
                queue.offer(new int[]{ni, nj});
                vis[ni][nj] = true;
                count++;
            }
        }
    }
    return count;
}

Sword finger t29 clockwise print matrix

Defines whether a two-dimensional array has been accessed, and changes the left side of the row and column every time

int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int directionIndex = 0;
for (int i = 0; i < total; i++) {
	order[i] = matrix[row][column];
	visited[row][column] = true;
	int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
	if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
	directionIndex = (directionIndex + 1) % 4;
	}
	row += directions[directionIndex][0];
	column += directions[directionIndex][1];
}

Search by layer

be careful:

Array equal to null is different from length equal to 0. Judge whether it is null first
During the 3rd and 4th searches on each layer, first check whether there is only one row or column, otherwise the search will be repeated

public int[] spiralOrder(int[][] matrix) {
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
        return new int[0];
    }
    int rows = matrix.length;
    int columns = matrix[0].length;
    int[] ans = new int[rows * columns];
    int index = 0;
    int left = 0, right = columns-1, top = 0, bottom = rows-1;
    while (left <= right && top <= bottom) {
        // Search in four directions
        for (int i = left; i <= right; i++) {
            ans[index++] = matrix[top][i];
        }
        for (int j = top+1; j <= bottom; j++) {
            ans[index++] = matrix[j][right];
        }
        // Prevent repeated searches when there is only one row or one column
        if (left < right && top < bottom) {
            for (int i = right-1; i >= left; i--) {
                ans[index++] = matrix[bottom][i];
            }
            for (int j = bottom-1; j > top; j--) {
                ans[index++] = matrix[j][left];
            }
        }
        left++;
        right--;
        top++;
        bottom--;
    }
    return ans;
}

9. Stack related

q20 valid parentheses

Why does the stack here use double ended queues?
```
Deque<Character> stack = new LinkedList<Character>();
```
Since Vector has been abandoned due to efficiency problems, the Stack inherited from Vector also has efficiency problems, so it is not recommended.

Another reason is that deque double ended queue can realize a variety of data structures, which can be simulated as a stack structure. Deque is very upmarket, with upper in and upper out, upper in and lower out, and even lower in and upper out. Only you can't think of it, and I can't do it.

Understand Java's collection framework and polymorphism (join the army for the father)

Here, the Map code is more concise
```
Map<Character, Character> pairs = new HashMap<Character, Character>() {{
    put(')', '(');
    put(']', '[');
    put('}', '{');
}};
```
Implementation of queue with stack in q232

It's not as complicated as I thought. When you exit the stack directly from the stack on the right, enter the stack to judge whether the stack on the left is full, and then enter the left.

It is similar to the implementation of stack with queue. It mainly deals with the operation of entering the stack and entering the queue
q155 minimum stack

At first, I thought it was simple to record the minimum value of the current stack or the position pointing to the minimum value every time, but I ignored that the minimum value may be restored after leaving the stack, so I must record the minimum value every time, and open up a unified stack space to retain the minimum value of the stack at each position

Or another stack space holds elements that are not strictly decremented

Note: in Math.min(Integer.MIN_VALUE, Integer.MAX_VALUE) operation, Integer.MAX_VALUE is the minimum value
Push in pop-up sequence of sword finger t31 stack

Two previous mistakes
1. Don't remember to while out of the stack
2. Before stack.peek in while, ensure that the stack is not empty, otherwise it is a null pointer exception
Where two compilers help me optimize
1. Finally, when you return, you don't need if(stack.isEmpty()) and else, just return
2. If the loop index value is not used inside the for loop, it is more concise to use enhanced for instead
```
public boolean validateStackSequences(int[] pushed, int[] popped) {
    // Simulate a stack and check whether it is empty according to push and pop operations
    Deque<Integer> stack = new LinkedList<>();
    int i = 0;
    for (int k : pushed) {
        stack.push(k);
        while (!stack.isEmpty() && stack.peek() == popped[i]) {
            stack.pop();
            i++;
        }
    }
    return stack.isEmpty();
}
```

10. Team related

q225 imitate stack with queue

Only the push operation is special. Two queues are established. For each element in the queue, all elements in the other queue must be added to the team. In fact, all elements added to the team are stacked. In the interaction of two queues, because of the novelty of the team, the "stack" can only be processed one by one

class MyStack {
Queue queue1;
Queue queue2;

class MyStack {
    Queue<Integer> queue1;
    Queue<Integer> queue2;

    /** Initialize your data structure here. */
    public MyStack() {
        queue1 = new LinkedList<Integer>();
        queue2 = new LinkedList<Integer>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        queue2.offer(x);
        while (!queue1.isEmpty()) {
            queue2.offer(queue1.poll());
        }
        Queue<Integer> temp = queue1;
        queue1 = queue2;
        queue2 = temp;
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue1.poll();
    }
    
    /** Get the top element. */
    public int top() {
        return queue1.peek();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue1.isEmpty();
    }
}

11. Dynamic planning

Characteristics that can be solved with dynamic specifications
1. optimizable
2. Decomposable into subproblems
3. The subproblem can be decomposed into smaller subproblems
4. Analyze problems from top to bottom and solve problems from bottom to top
5. Store small problems that have been solved
6. If we can mathematically prove that a case is the optimal solution, we can use greed
q5 longest palindrome string
1. Write the state transition equation and two boundary conditions to solve the problem
  1. P(i,j)=P(i+1,j−1)∧(Si==Sj)
  2. {P(i,i)=true；P(i,i+1)=(Si==Si+1)
2. thinking
  1. initialization
```
for (int i = 0; i < len; i++) {
    dp[i][i] = true;
}
```
  2. Loop method, boundary size from small to large loop
```
//The iteration starts with a substring length of 2
for(int L=2; L <= len; L++){
    // Left boundary
    for (int i = 0; i < len; i++) {
        // Right boundary
        int j = i+L-1;
```
  3. As a result, the dp value is true and the left and right boundaries are the largest
```
if (dp[i][j] && j - i + 1 > maxLen) {
    maxLen = j - i + 1;
    begin = i;
}
```
3. The center expansion algorithm can be used to expand from the middle (boundary conditions) to both sides each time
q55 jump game

Without looking at the parsing, it is a dynamic programming algorithm. It applies for a bool type array with a length of nums, two for loops, sets the reachable to true, and returns the bool value of the last position. In fact, it can be done greedily. Just maintain the farthest subscript max that can be reached. Note I < = max
```
public boolean canJump(int[] nums) {
    int len = nums.length;
    int max = 0;
    for (int i = 0; i < Math.min(len, max+1); i++) {
        max = Math.max(max, i+nums[i]);
        if(max>=len-1){
            return true;
        }
    }
    return false;
}
```
q72 edit distance difficulty dp
q96 different binary search trees

First understand the definition of binary search tree: it is either an empty tree or a binary tree with the following properties: if its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node; if its right subtree is not empty, the values of all nodes on the right subtree are greater than the values of its root node; its left and right subtrees are also binary sort trees respectively.

According to the dynamic programming solution, the state transition equation is found

G(n)=i=1∑n**F(i,n) (1)

F(i,n)=G(i−1)⋅G(n−i) (2)

G(n)=i=1∑n**G(i−1)⋅G(n−i) (3)

Apply for one more bit in the array

Q339 word splitting

A jump version of the dp problem, in fact, the solution is the same, but this one-dimensional array needs two for loops to determine

dp[i]=dp[j] && check(s[j...i−1])

for (int i = 1; i < s.length() + 1; i++) {
    for (int j = 0; j < i; j++) {
        if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
            dp[i] = true;
            break;
        }
    }
}

q152 product maximum subarray

A typical mistake is made: the optimal solution of the current position of this problem may not be obtained by the transfer of the optimal solution of the previous position, such as [- 2, 3, - 4]

Each traversal should record the maximum and minimum values ending with the current node

max(num[i], num[i]*mx, num[i]*mn)

public int maxProduct(int[] nums) {
    int[] maxf = new int[nums.length];
    int[] minf = new int[nums.length];
    maxf[0] = nums[0];
    minf[0] = nums[0];
    int max = nums[0];
    for (int i = 1; i < nums.length; i++) {
        maxf[i] = Math.max(Math.max((nums[i] * minf[i-1]), nums[i]), Math.max((nums[i] * maxf[i-1]), nums[i]));
        minf[i] = Math.min(Math.min((nums[i] * minf[i-1]), nums[i]), Math.min((nums[i] * maxf[i-1]), nums[i]));
        max = Math.max(max, maxf[i]);
    }
    return max;
    
    // The following method can reduce the space complexity to O(1). Since the ith state is only related to the ith − 1 state, according to the idea of "rolling array", we can only use two variables to maintain the state at the time of i − 1, one to maintain fmax and the other to maintain fmin. Other similar dynamic programming problems can also be optimized in this way
    
    int maxf = nums[0];
    int minf = nums[0];
    int max = nums[0];
    for (int i = 1; i < nums.length; i++) {
        int mx = maxf, mn = minf;
        maxf = Math.max(mx * nums[i], Math.max(nums[i], mn * nums[i]));
        minf = Math.min(mn * nums[i], Math.min(nums[i], mx * nums[i]));
        max = Math.max(maxf, max);
    }
    return max;
}

q198 house raiding

The original dp array is the largest, and does not necessarily include the current number

So the state transition formula is dp[i] = Math.max(dp[i-2] + nums[i], dp[i-1])

public int rob(int[] nums) {
    int len = nums.length;
    if(len == 0) {
        return 0;
    }
    if(len == 1) {
        return nums[0];
    }
    int[] dp = new int[len];
    dp[0] = nums[0];
    dp[1] = Math.max(nums[0], nums[1]);
    for (int i = 2; i < len; i++) {
        dp[i] = Math.max(dp[i-2] + nums[i], dp[i-1]);
    }
    return Math.max(dp[len - 1], dp[len-2]);
}

Dynamic programming can often optimize the spatial complexity. Rolling arrays can be used. At each time, only the maximum total amount of the first two houses needs to be stored

int left = nums[0];
int right = Math.max(nums[0], nums[1]);
for (int i = 2; i < len; i++) {
    int new_right = Math.max(left + nums[i], right);
    left = right;
    right = new_right;
}
return right;

q221 maximum square

I didn't think of his state transition equation: dp(i,j)=min(dp(i − 1,j),dp(i − 1,j − 1),dp(i,j − 1)) + 1

This state transition equation exists only when = = ='1 '

There is no need to consider the boundary condition here. If (I = = 0 | J = = 0) is the boundary condition

The result is not the last one of dp, but the square of its maximum

java initializes the int array to all zeros by default
```
for (int i = 0; i < r; i++) {
    for (int j = 0; j < c; j++) {
        if (matrix[i][j] == '1') {
            if (i == 0 || j == 0) {
                dp[i][j] = 1;
            } else {
                dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;
            }
            maxSide = Math.max(maxSide, dp[i][j]);
        }

    }
}
```

279 perfect square

I thought of the state transition equation, but it won't be transformed into code

i don't know how to find the complete square next to the sum of squares. A for loop keeps looking, as long as it is smaller than i

public int numSquares(int n) {
    int dp[] = new int[n + 1];
    for (int i = 0; i <= n; i++) {
        dp[i] = i;
        for (int j = 0; j * j <=  i; j++) {
            dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

q300 longest ascending subsequence
1. Ordinary dp
  
  dp[i]=max(dp[j])+1, where 0 ≤ J < I and num [J] < num [i]
  
  The minimum value of dp at each position is 1. It is not necessary to define it as negative infinity
```
dp[i] = Math.max(dp[i], dp[j] + 1);
```
2. Greedy + binary optimization can be used
  
  Maintain a monotonically increasing sequence with D [], scan backward, and the number newly added each time is as small as possible. If num [i] > d [len], update len = len + 1, otherwise use dichotomy to find the ordinal number in front of D [], find the subscript i satisfying D [I - 1] < num [J] < d [i], and update d [i] = num [J]
  
  [the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-cxnxdqar-1637714619661) (C: / users / chenzhijian / appdata / roaming / typora / typora user images / image-20211103111050368. PNG)]
  
  Binary search can be used not only to find certain numbers, but also here
```
public int lengthOfLIS(int[] nums) {
    int len = 1, n = nums.length;
    if (n == 0) {
        return 0;
    }
    // The same number will replace the same number
    int[] d = new int[n + 1];
    d[1] = nums[0];
    for (int i = 1; i < n; i++) {
        if (nums[i] > d[len]) {
            d[++len] = nums[i];
        } else {
            int l = 1, r = len, pos = 0;
            //Start dichotomy to find the nearest position less than it
            while (l <= r) {
                int mid = (l + r) / 2;
                if (nums[i] > d[mid]) {
                    pos = mid;
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
            d[pos + 1] = nums[i];
        }
    }
    return len;
}
```
The best time to buy and sell stocks includes the freezing period

Use f[i] to represent the "cumulative maximum return" after the end of day I. there are three states
1. We currently hold a stock, and the corresponding "cumulative maximum return" is recorded as f[i] [0];
2. At present, we do not hold any stocks and are in the freezing period. The corresponding "cumulative maximum return" is recorded as f[i] [1];
3. At present, we do not hold any shares and are not in the freezing period. The corresponding "cumulative maximum return" is recorded as f[i] [2].
f[i] [0] = max(f[i-1] [0], f[i-1] [2] - prices[i])

I held a stock yesterday and did not sell it or was not in the freezing period yesterday. I bought it today

f[i] [1] = f[i-1] [0]+prices[i]

It was sold yesterday, so it's in the freezing period

f[i] [2] = max(f[i-1] [1], f[i-1] [2])

It was sold just yesterday or before yesterday

The final answer is max(f[n-1] [1], f[n-1] [2]). Holding stocks on the last day is meaningless, and the freezing period represents that day, so it is the last one
```
public int maxProfit(int[] prices) {
        if (prices.length == 0) {
            return 0;
        }

        int n = prices.length;
        // f[i][0]: maximum return from holding stocks
        // f[i][1]: the cumulative maximum return of not holding stocks and in the freezing period
        // f[i][2]: the cumulative maximum return that does not hold stocks and is not in the freezing period
        int[][] f = new int[n][3];
        f[0][0] = -prices[0];
        for (int i = 1; i < n; ++i) {
            f[i][0] = Math.max(f[i - 1][0], f[i - 1][2] - prices[i]);
            f[i][1] = f[i - 1][0] + prices[i];
            f[i][2] = Math.max(f[i - 1][1], f[i - 1][2]);
        }
        return Math.max(f[n - 1][1], f[n - 1][2]);
    }
```
Spatial optimization

f[i] [?] is only related to f[i-1] [?] and has nothing to do with f[i-2] [?] and all previous states, so you only need to store f[i-1] [?] in three variables
```
int n = prices.length;
        int f0 = -prices[0];
        int f1 = 0;
        int f2 = 0;
        for (int i = 1; i < n; ++i) {
            int newf0 = Math.max(f0, f2 - prices[i]);
            int newf1 = f0 + prices[i];
            int newf2 = Math.max(f1, f2);
            f0 = newf0;
            f1 = newf1;
            f2 = newf2;
        }

        return Math.max(f1, f2);
```
- Dynamic programming and space can be optimized in one dimension

q322 change

The direct use of backtracking will timeout, and the memory search needs to be done with the help of array, which belongs to the top-down optimization

State transition equation F(S)=F(S − C)+1

public int coinChange(int[] coins, int amount) {
        return coinChange(coins, amount, new int[amount]);
    }

    // Recursion is to borrow money and let future generations repay it
    private int coinChange(int[] coins, int amount, int[] count) {
        if (amount < 0) {
            return -1;
        }
        if (amount == 0) {
            return 0;
        }
        if (count[amount-1] != 0) {
            return count[amount-1];
        }
        int min = Integer.MAX_VALUE;
        for (int coin : coins) {
            int res = coinChange(coins, amount - coin, count);
            if (res >= 0 && res < min) {
                min = res + 1;
            }
        }
        count[amount-1] = min == Integer.MAX_VALUE ? -1 : min;
        return count[amount-1];
        // This is the case without memory search
//        return min == Integer.MAX_VALUE ? -1 : min;
    }

Bottom up dynamic programming

F(i)=minF(i−cj)+1 j=0...n−1

My writing

public int coinChange(int[] coins, int amount) {
    int[] dp = new int[amount+1];
    dp[0] = 0;
    for (int i = 1; i <= amount; i++) {
        int min = Integer.MAX_VALUE;
        for (int coin : coins) {
            if (i-coin >= 0 && dp[i-coin] < min && dp[i-coin] >= 0) {
                dp[i] = dp[i-coin]+1;
                min = dp[i-coin];
            }
        }
        if (min == Integer.MAX_VALUE) {
            dp[i] = -1;
        }
    }
    return dp[amount];
}

The official solution is more ingenious. The array is initially assigned as amount + 1, which is convenient to find the minimum value

public int coinChange(int[] coins, int amount) {
        int max = amount + 1;
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, max);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            for (int j = 0; j < coins.length; j++) {
                if (coins[j] <= i) {
                    dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }

q416 split equal sum subset

In fact, it can be transformed into 01 knapsack problem. The number inside can be combined into exactly half of the total. In dp, the behavior selects or deselects this number and lists it as the total

When dp is initialized, when the capacity is given to n bits and n+1 bits, the rows here are given to N and the columns are given to n+1, because n+1 is convenient for operation

Return false

One number is more than half the total
There are only 1 or 0 numbers
The sum is odd

Judge whether the current number is greater than half of the total. You can judge less if (J > = num [i])

public boolean canPartition(int[] nums) {
        // Calculate sum
        int sum = 0, max = 0, n = nums.length;
        if (n < 2) {
            return false;
        }
        for (int i = 0; i < n; i++) {
            sum += nums[i];
            max = Math.max(max, nums[i]);
        }
        if (sum % 2 == 1) {
            return false;
        }
        int halfSum = sum / 2;
        if (max > halfSum) {
            return false;
        }
        boolean[][] dp = new boolean[n][halfSum + 1];

        // Initialization, the following step can be omitted
//        for (int i = 0; i < n; i++) {
//            dp[i][0] = true;
//        }
        dp[0][nums[0]] = true;

        for (int i = 1; i < n; i++) {
            for (int j = 1; j <= halfSum; j++) {
                if (j >= nums[i]) {
                    dp[i][j] = dp[i-1][j] | dp[i-1][j-nums[i]];
                } else {
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[n-1][halfSum];
    }

Sword fingers t46 translate numbers into strings, similar to climbing stairs

Conventional dp writing

String s = String.valueOf(num);
int[] dp = new int[s.length()+1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= s.length(); i++) {
    String tmp = s.substring(i-2, i);
    // This compares the string size
    if (tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0) {
        dp[i] = dp[i-2] + dp[i-1];
    } else dp[i] = dp[i-1];
}
return dp[s.length()];

dp optimized writing method

String s = String.valueOf(num);
//a is equivalent to dp[i-2] b is equivalent to dp[i-1] c is equivalent to dp[i]
int a = 1,b = 1,c;
for (int i = 2; i <= s.length(); i++) {
    String tmp = s.substring(i-2, i);
    c = (tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0) ? a + b : b;
    a = b;
    b = c;
}
return b;

dfs writing method

Writing method 1:
	public int translateNum(int num) {
        //Convert string to number
        String str = String.valueOf(num);
        //dfs traversal string solution
        return dfs(str, 0);
    }
    //Indicates that there are many translation methods starting from the index position
    public int dfs(String str, int index){
        //If the current subscript is greater than or equal to the length of the string - 1, it indicates that the current position jumped here from the last time, and 1 is returned directly
        if(index >= str.length() - 1)
            return 1;
        //First solve the number of methods that translate one character at a time
        int res = dfs(str, index + 1);
        //Start with the subscript of the current character, intercept two digits, and judge whether the composed number is between 10 and 25
        //If you can translate two characters directly at this time, then start the translation from the position after the two characters
        String temp = str.substring(index, index + 2);
        if(temp.compareTo("10") >= 0 && temp.compareTo("25") <= 0)
            res += dfs(str, index + 2);
        return res;
    }
Method 2:
    int translateNum(int num) {
        return f(num);
    }

    int f(int num) {
        if (num < 10) {
            return 1;
        }
        if (num % 100 < 26 && num % 100 > 9) {
            return f(num / 10) + f(num / 100);
        } else {
            return f(num / 10);
        }
    }

12. Bit operation

Number of 1 in binary
1. Move the number to the right and compare it with 1
2. Compare with 1, shift left and compare again (prevent negative numbers)
3. -1 and itself until it is 0
q128 is a number that appears only once

The nature of using XOR

(a1⊕a1)⊕(a2⊕a2)⊕⋯⊕(a**m⊕a**m)⊕a**m+1

0⊕0⊕⋯⊕0⊕a**m+1=a**m+1
q338 bit count
1. If i is an even number, then f(i) = f(i/2)
  If i is an odd number, then f(i) = f(i - 1) + 1
2. Brian Kernighan algorithm
  
  while (x > 0){x &= (x - 1);ones++;}
3. Highest bit
  
  For example, s(13) = s(8) + s(5), 8 is the highest bit of 13, and there is only one 1 in it. I didn't expect the method to quickly find the most significant bit. I thought it would need extra calculation every time. In fact, it can depend on the traversal process, using the algorithm of 2
```
public int[] countBits(int n) {
    int[] dp = new int[n+1];
    dp[0] = 0;
    int highBit = 0;
    for (int i = 1; i < n + 1; i++) {
        // Find the most significant bit of i
        if ((i & (i-1)) == 0) {
            highBit = i;
        }
        dp[i] = dp[i - highBit] + 1;
    }
    return dp;
}
```
4. Lowest bit
  
  If xx is an even number, bits[x] = bits[x/2]
  
  If xx is an odd number, bits[x] = bits[x/2]+1
  
  bits[i] = bits[i >> 1] + (i & 1);
5. The lowest setting bit is essentially the algorithm of method 2
  
  y = x & (x-1) => bits[x] = bits[y] + 1
  
  bits[x] = bits[x&(x-1)] + 1
q461 Hamming distance

The reason why I can't do it is because I don't know that there is a bitwise and operator. This is the basis of this problem. z = x ^ y, just find the number of digits of 1 of z. Whether it's wheel adjustment or Brian Kernighan algorithm

Integer power of sword finger t16 array

This question tests the consideration of various special values and the accelerated optimization of the algorithm

Recursive Method

public double myPow(double x, int n) {
        if (x == 0 && n < 0) {
            return 0;
        }
        long absEx = n;
        if (n < 0)  absEx = -absEx;  // Cannot use absEx = -n, different types
        double res = getPow(x, absEx);
        if (n < 0) {
            res = 1 / res;
        }
        return res;
}

private double getPow(double x, long absEx) {
        //Recursive exit
        if (absEx == 0) {
            return 1;
        }
        if (absEx == 1) {
            return x;
        }
        double ans = getPow(x, absEx>>1);
        ans *= ans;
        // absEx odd or even
        if ((absEx & 1) == 1) {
            ans *= x;
        }
        return ans;
}

Fast power analysis

double res = 1.0;
while (absEx > 0) {
    if ((absEx & 1) == 1) {
        res *= x;
    }
    x *= x;
    absEx >>= 1;
}
return res;

13. Backtracking

Backtracking, depth first, recursion, dynamic programming
1. Backtracking usually uses the simplest recursion. "Backtracking algorithm" emphasizes the use of the idea of "depth first traversal". It uses a changing variable to search the required results in the process of trying various possibilities. The rationality of fallback operation for search is emphasized.
2. Depth first search: when the edges of node v have been explored, the search will be traced back to the starting node of the edge where node v is found.
3. Dynamic programming only requires us to evaluate how much the optimal solution is, and what the specific solution corresponding to the optimal solution is not required. Therefore, it is suitable for evaluating the effect of a scheme
4. When to use the used array and when to use the begin variable
  
  For the arrangement problem, pay attention to the order (that is, when [2,2,3] and [2,3,2] are regarded as different lists), it is necessary to record which numbers have been used. In this case, use the used array;
  The combination problem does not pay attention to the order (that is, when [2,2,3] and [2,3,2] are regarded as the same list), it needs to search in a certain order. In this case, use the begin variable.
t22 bracket generation
1. The simplest is the violence law. Start with 2*n '(' and judge whether it is reasonable every time it is full
  - The reasonable judgment function is: add one in the left bracket and subtract one in the right bracket. If it is less than zero in the middle, it is unreasonable, and the final result is zero
2. Backtracking method
  
  If the number of left parentheses is not greater than n, we can put an left parenthesis. If the number of right parentheses is less than the number of left parentheses, we can put a right parenthesis. There is no need to judge
```
public void backtrack(List<String> res, StringBuilder cur, int open, int close, int max){
    // Get a result
    if(cur.length() == 2*max){
        res.add(cur.toString());
        return;
    }
    if(open < max){
        cur.append('(');
        backtrack(res, cur, open+1, close, max);
        cur.deleteCharAt(cur.length()-1);
    }
    if(close < open){
        cur.append(')');
        backtrack(res, cur, open, close+1, max);
        cur.deleteCharAt(cur.length()-1);
    }
}
```

q39 array sum

The key idea of this problem is how to draw this backtracking tree. Take target as the root node of the tree, subtract the value of a candidate as the child node, and the leaf node with zero result is a solution

code

public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if(len == 0){
            return res;
        }
        Deque<Integer> path = new ArrayDeque<>();
        dfs(candidates, 0, len, target, path, res);
        return res;
    }

	/**
     * @param candidates Candidate array
     * @param begin      Search starting point
     * @param len        Redundant variables are attributes in candidates and can not be passed
     * @param target     Every time you subtract an element, the target value becomes smaller
     * @param path       The path from the root node to the leaf node is a stack
     * @param res        Result set list
     */
    private void dfs(int[] candidates, int start, int len, int target, Deque<Integer> path, List<List<Integer>> res) {
        if(target<0){
            return;
        }
        if(target==0){
            res.add(new ArrayList<>(path));
            return;
        }
        // Focus on understanding the semantics of searching from begin here
        for (int i = start; i < len; i++) {
            path.addLast(candidates[i]);
            // Note: since each element can be reused, the starting point of the next round of search is still i, which is very easy to make mistakes here
            dfs(candidates, i, len, target-candidates[i], path, res);
            path.removeLast();
        }
      }
    }

prune:

Sort first and start detection in the for loop

if(target-candidates[i]<0){
    break;
}

Recursive exits with target less than 0 can be deleted

q46 full arrangement

Parameters passed recursively are

Candidate array, array length (also derived from candidate array), recursion depth, path in recursion, result set list

If there are duplicate elements, two methods are used to remove the duplicate. One is to judge the duplicate before adding the result set (Sword finger t38 timeout). The other is to sort first. If it is the same as the previous one, skip it

Following the recursive routine of the previous question, I have two main problems
1. After recursion, the path does not remember to remove the last one
2. res.add(path); if there is a problem with the writing method, it should be written as res.add (New ArrayList < > (path)); see the following for details:
java knowledge points:

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-xrfhceh2-1637714619663) (C: / users / chenzhijian / appdata / roaming / typora / typora user images / image-20211012200830758. PNG)]

The above ls is a new pointer to list1, similar to

ArrayList ls = new ArrayList();

ls = list1

After path enters the parameter, it means that different pointers point to the same address. Each time add goes in, it points to the same address. Therefore, once the value in that address changes, all the values in res will change together. Finally, after returning to the root node, it will become an empty array

There is another way of thinking. The official analysis of 38 questions of sword finger offer. The number after the Interactive start and the number after it must not be repeated. During recursion, the original char [] array changes
```
class Solution {
      List<String> rec;
      boolean[] used;

    public String[] permutation(String s) {
        char[] ch = s.toCharArray();
        StringBuilder str = new StringBuilder();
        rec = new ArrayList<>();
        used = new boolean[s.length()];
        Arrays.sort(ch);
        dfs(ch, 0, str);
        String[] ans = new String[rec.size()];
        for (int i = 0; i < rec.size(); i++) {
            ans[i] = rec.get(i);
        }
        return ans;
    }

      private void dfs(char[] ch, int deep, StringBuilder str) {
          int length = ch.length;
          if (deep == length) {
              String s = new String(ch);
              if (!rec.contains(s)) {
                  rec.add(s);
              }
          }
          for (int i = deep; i < length; i++) {
              swap(ch, deep, i);
              dfs(ch, deep+1, str);
              swap(ch, deep, i);
//              if (used[i] || (i > 0 && !used[i - 1] && ch[i - 1] == ch[i])) {
//                  continue;
//              }
//              used[i] = true;
//              str.append(ch[i]);
//              dfs(ch, deep+1, str);
//              used[i] = false;
//              str.deleteCharAt(str.length()-1);
          }
      }

      private void swap(char[] ch, int i, int j) {
        char temp = ch[i];
        ch[i] = ch[j];
        ch[j] = temp;
      }
  }
```
q53 maximum suborder sum

A simple dynamic programming problem, the key is how to find the state transition equation

There should be no aftereffect when selecting sub problems
- Sub question 1: what is the maximum sum of continuous sub arrays ending with - 2;
- Sub question 2: what is the maximum sum of continuous sub arrays ending with - 1;
- ...
There is a link between these sub problems

There was a problem that I didn't figure out before. I thought that the maximum sum of continuous sub arrays ending with a certain number is the previous maximum. In fact, if this number is less than zero, it must be less than the previous number

You can use divide and conquer to solve this problem. Try to write it later

q78 subset

The first thought is recursion, which can set q46 fully arranged templates. The official solution is a little different

List<List<Integer>> ans = new ArrayList<>();
List<Integer> t = new ArrayList<>();

public List<List<Integer>> subsets(int[] nums) {
    dfs(0, nums);
    return ans;
}

private void dfs(int cur, int[] nums){
    if (cur == nums.length) {
        ans.add(new ArrayList<Integer>(t));
        return;
    }
    t.add(nums[cur]);
    dfs(cur + 1, nums);
    t.remove(t.size() - 1);
    dfs(cur + 1, nums);
}

The path in the middle and the traversal of the result set are placed in the global, and len is recalculated in the recursion, so three variables are written less in the recursion

The difference is that you don't need a for loop, but it's more difficult to write a recursive function

Conventional recursive writing

public List<List<Integer>> subsets(int[] nums) {
    List<List<Integer>> ans = new ArrayList<>();
    dfs(0, nums, new ArrayList<Integer>(), ans);
    return ans;
}

private void dfs(int cur, int[] nums, ArrayList<Integer> t, List<List<Integer>> ans){
    ans.add(new ArrayList<Integer>(t));
    for (int i = cur; i < nums.length; i++) {
        t.add(nums[i]);
        dfs(i + 1, nums, t, ans);
        t.remove(t.size() - 1);
    }
}

Another way to solve this problem is to use binary

Take 123 as an example, 011 –'23'101 –'13 '

14. Recursion

Postorder traversal sequence of sword finger t33 binary search tree

The root is on the far right, and the dividing point of the left and right subtrees is the first number larger than the root

public boolean verifyPostorder(int[] postorder) {
    return verify(postorder, 0, postorder.length - 1);
}

  private boolean verify(int[] postorder, int i, int j) {
    if (i >= j) return true;
    int p = i;
    while (postorder[p] < postorder[j]) p++;
    int m = p;
    while (postorder[p] > postorder[j]) p++; // Let p a round of swimming to see if the left is smaller than root and the right is larger than root
    return p == j && verify(postorder, i, m - 1) && verify(postorder, m, j-1); // Such a return value is often used when the left and right subtrees need to meet the conditions at the same time
  }
}

Sword finger t36 binary search tree and bidirectional linked list

right key

Node head, pre;
public Node treeToDoublyList(Node root) {
    if (root == null) {
        return null;
    }
    treeToDoublyList1(root);
    pre.right = head;
    head.left =pre;//The order of these two sentences can also be reversed by pointing to each other between the head node and the tail node

    return head;

}

// Medium order traversal
private void dfs(Node cur) {
    if (cur == null) {
        return;
    }
    dfs(cur.left);
    // pre is the previous cur of the current node and is used to convert it into a two-way linked list
    if (pre == null) {
    	// Head
        head = cur;
    } else {
        pre.right = cur;
        cur.left = pre;
    }
    // Automatically updates to the tail
    pre = cur;
    dfs(cur.right);
}

My wrong answer

If root is returned, the output will ignore the right subtree of the left child and the left subtree of the right child

public Node treeToDoublyList1(Node root) {
    if (root == null) {
        return null;
    }
    Node left = treeToDoublyList1(root.left);
    if (pre == null) {
        head = root;
    }
    if (left != null) {
        left.right = root;
        root.left = left;
    }
    pre = root;
    Node right = treeToDoublyList1(root.right);
    if (right != null) {
        root.right = right;
        right.left = root;
    }
    return root;
}

Keywords: Java Algorithm leetcode Dynamic Programming dfs

Added by deejay1111 on Wed, 24 Nov 2021 18:54:55 +0200

Programming VIP