leetcode of algorithm interview in Dachang 22. Dictionary tree
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
Trie tree, namely dictionary tree, also known as prefix tree, is a tree structure. Its typical application is to count and sort a large number of strings (but not limited to strings), so it is often used by search engines for text word frequency statistics. Its priority is to minimize unnecessary string comparison and improve search efficiency.
The core idea of Trie is to exchange space for time, and use the public prefix of string to reduce the overhead of query time, so as to improve efficiency
Basic properties
- The root node does not contain characters, and each node contains only one character except the following node
- From the root node to a node, the characters passing through the path are connected to the corresponding string of the node
- All child nodes of each node contain different characters

Practical applications, such as search
208. Implement Trie (prefix tree)(medium)

- Idea: the length of this character set is 26, that is, 26 lowercase English letters. isEnd indicates whether the node is the end of the string.
- Insert string: start from the root node of the field tree. If the child node exists, continue to process the next character. If the child node does not exist, create a child node to the corresponding position of children, move backward along the pointer, and process the next character. Take inserting 'cad' as an example
- Find prefix: starting from the root node, if the child node exists, continue to search the next child node along the pointer until the last one. If all characters of the prefix are found, it indicates that the dictionary tree contains the prefix. If the child node does not exist, the prefix is not included in the dictionary tree, and false is returned.
- Lookup string: the same as the lookup prefix, except that the isEnd of the last returned node is true, that is, the string is just a branch of the dictionary tree
- Complexity analysis: time complexity, initialization as O(1), other operations as O(S), and s as the length of the string. The space complexity is O(T), and t is the size of the character set. This problem is 26
js:
var Trie = function() {
this.children = {};
};
Trie.prototype.insert = function(word) {
let nodes = this.children;
for (const ch of word) {//Circular word
if (!nodes[ch]) {//If the current character is not in the child node, a response position from the child node to the children is created
nodes[ch] = {};
}
nodes = nodes[ch];//Moves the pointer to the next character child node
}
nodes.isEnd = true;//End of character
};
Trie.prototype.searchPrefix = function(prefix) {
let nodes = this.children;
for (const ch of prefix) {//Cyclic prefix
if (!nodes[ch]) {//The current character is not in the child node and returns false directly
return false;
}
nodes = nodes[ch];//Moves the pointer to the next character child node
}
return nodes;//Returns the last node
}
Trie.prototype.search = function(word) {
const nodes = this.searchPrefix(word);
//Judge whether the node returned by searchPrefix is the character at the end of the string
return nodes !== undefined && nodes.isEnd !== undefined;
};
Trie.prototype.startsWith = function(prefix) {
return this.searchPrefix(prefix);
};
Java:
//java
class Trie {
private Trie[] children;
private boolean isEnd;
public Trie() {
children = new Trie[26];
isEnd = false;
}
public void insert(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true;
}
public boolean search(String word) {
Trie node = searchPrefix(word);
return node != null && node.isEnd;
}
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;
}
private Trie searchPrefix(String prefix) {
Trie node = this;
for (int i = 0; i < prefix.length(); i++) {
char ch = prefix.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
return null;
}
node = node.children[index];
}
return node;
}
}
212. Word search II (hard)
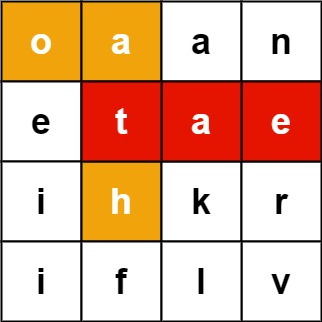
- Idea: add all strings in the words array to the Trie, then traverse the grid, judge whether the string formed by the grid path is in the Trie, and then keep backtracking in the up, down, left and right directions.
- Complexity analysis: time complexity O(MN ⋅ 3^L), space complexity O(max(MN, KL)), visited space O(MN), dictionary tree O(KL), l is the length of the longest string, and K is the length of the words array. The maximum depth of dfs recursive stack is O(min(L,MN)),
Method 1.Trie
Js:
var findWords = function (board, words) {
const trie = new Trie();
const dxys = [
[0, -1],
[-1, 0],
[0, 1],
[1, 0],
];
const xLen = board.length,
yLen = board[0].length;
const visited = {};
const ret = [];
// Build Trie
for (let word of words) {
trie.insert(word);
}
// DFS board
const dfs = (x, y, nodes, str) => {
if (nodes[board[x][y]].isEnd) {
ret.push(str + board[x][y]);
// Set to false to prevent repetition and add the string to ret
nodes[board[x][y]].isEnd = false;
}
// Process the status of this layer
nodes = nodes[board[x][y]];
str += board[x][y];
// Search in four directions
visited[x * 100 + y] = true;
for (let [dx, dy] of dxys) {
const newX = x + dx,
newY = y + dy;
if (
newX < 0 ||
newY < 0 ||
newX >= xLen ||
newY >= yLen ||
!nodes[board[newX][newY]] ||
visited[newX * 100 + newY]
)
continue;
dfs(newX, newY, nodes, str);
}
visited[x * 100 + y] = false;
};
for (let x = 0; x < xLen; x++) {
for (let y = 0; y < yLen; y++) {
if (trie.children[board[x][y]]) dfs(x, y, trie.children, "");
}
}
return ret;
};
var Trie = function () {
this.children = {};
};
Trie.prototype.insert = function (word) {
let nodes = this.children;
for (const ch of word) {//Circular word
if (!nodes[ch]) {//If the current character is not in the child node, a response position from the child node to the children is created
nodes[ch] = {};
}
nodes = nodes[ch];//Moves the pointer to the next character
}
nodes.isEnd = true;//End of character
};
Java:
class Solution {
int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
public List<String> findWords(char[][] board, String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
Set<String> ans = new HashSet<String>();
for (int i = 0; i < board.length; ++i) {
for (int j = 0; j < board[0].length; ++j) {
dfs(board, trie, i, j, ans);
}
}
return new ArrayList<String>(ans);
}
public void dfs(char[][] board, Trie now, int i1, int j1, Set<String> ans) {
if (!now.children.containsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
now = now.children.get(ch);
if (!"".equals(now.word)) {
ans.add(now.word);
}
board[i1][j1] = '#';
for (int[] dir : dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {
dfs(board, now, i2, j2, ans);
}
}
board[i1][j1] = ch;
}
}
class Trie {
String word;
Map<Character, Trie> children;
boolean isWord;
public Trie() {
this.word = "";
this.children = new HashMap<Character, Trie>();
}
public void insert(String word) {
Trie cur = this;
for (int i = 0; i < word.length(); ++i) {
char c = word.charAt(i);
if (!cur.children.containsKey(c)) {
cur.children.put(c, new Trie());
}
cur = cur.children.get(c);
}
cur.word = word;
}
}
720. The longest word in the dictionary (easy)
Method 1: sort+hash
- Idea: sort the array, and then traverse the string array to judge whether the substrings of each string in the array are in the array
- Complexity: time complexity O(mn), M is the length of string array, and n is the maximum length of string. Spatial complexity O(m)
js:
var longestWord = function (words) {
let set = new Set()
words.forEach(v => set.add(v))//set is easy to find
//Sort by length first, then by dictionary
words.sort((a, b) => a.length === b.length ? a.localeCompare(b) : b.length - a.length)
for (let i = 0; i < words.length; i++) {
let flag = true
for (let j = 1; j < words[i].length; j++) {
if (!set.has(words[i].substring(0, j))) {//Check whether there is each substring of the string in the set
flag = false
break
}
}
if (flag) {
return words[i]
}
}
return ''
};
java:
class Solution {
public String longestWord(String[] words) {
Set<String> wordset = new HashSet();
for (String word: words) wordset.add(word);
Arrays.sort(words, (a, b) -> a.length() == b.length()
? a.compareTo(b) : b.length() - a.length());
for (String word: words) {
boolean flag = true;
for (int k = 1; k < word.length(); ++k) {
if (!wordset.contains(word.substring(0, k))) {
flag = false;
break;
}
}
if (flag) return word;
}
return "";
}
}
Method 2: dictionary tree

- Idea: insert all strings into trie and recursively find the word with the largest length
- Complexity: time complexity O(mn), m is the length of string array, and n is the maximum length of string. Spatial complexity O(∑ w). The recursion depth will not exceed the maximum word length, and the spatial complexity of the field book is the sum of the lengths of all strings.
js:
var longestWord = function (words) {
const trie = new Trie()
words.forEach(word => {//Insert all strings into trie
trie.insert(word)
})
let res = ''
const _helper = (nodes, path) => {
if (path.length > res.length || (res.length === path.length && res > path)) {
res = path
}
//{a:{b1:{c1:{isEnd: true}},b2:{c2:{isEnd: true}}}}
for (const [key, value] of Object.entries(nodes)) {
if (value.isEnd) {//If the current character is the end of a string
path += key
_helper(value, path)//Recursive search
path = path.slice(0, -1)//to flash back
}
}
}
_helper(trie.children, '')//Recursively find the word with the largest length
return res
}
var Trie = function() {
this.children = {};
};
Trie.prototype.insert = function(word) {
let nodes = this.children;
for (const ch of word) {//Circular word
if (!nodes[ch]) {//If the current character is not in the child node, a response position from the child node to the children is created
nodes[ch] = {};
}
nodes = nodes[ch];//Moves the pointer to the next character
}
nodes.isEnd = true;//End of character
};