Leetcode one question per day (two questions) - 3.4 + 3.3
preface
I wrote the daily question of these two days, learned some new knowledge points, and made a comb and summary.
3.3 add up
Given a non negative integer num, the numbers on each bit are added repeatedly until the result is a single digit. Return this result.
Title Link 258. LeetCode (LeetCode CN. Com)
Advanced
Can you solve this problem within O(1) time complexity without using loops or recursion?
Analysis and thinking
First of all, it is easy to think of using two-level loop nesting. The outermost loop is used to judge whether the number is an integer from 0 to 9, and the inner loop is used to calculate the sum of each digit of the current number.
However, when I saw the advanced stage, I was really baffled.
Checked Official explanation After that, I learned some new knowledge points. First of all, the numbers of a number will eventually get a number from 0 to 9 after continuous addition. Of course, 0 is a special case. It can be obtained only when it is 0 at the beginning. This number is mathematically called the root of natural number.
Mathematical derivation
Here, let's assume that the number is num, and its digits are ai, (i = 1, 2, 3) i represents the number of bits from the first bit, that is, the result of each addition is temp
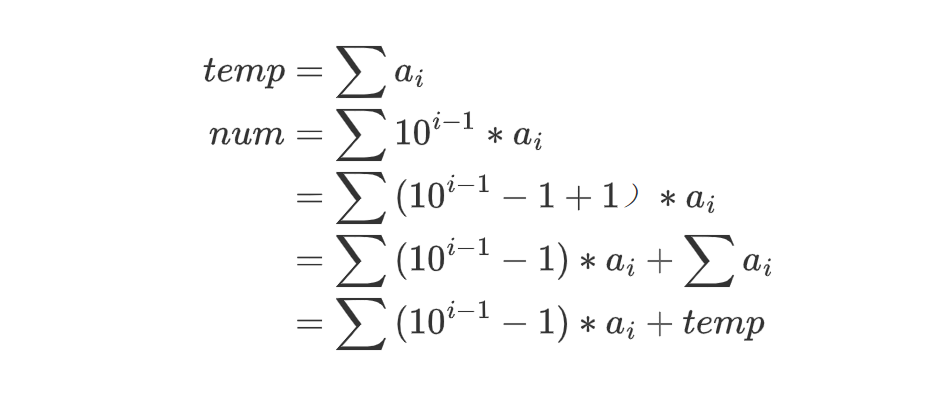
According to the formula, we can know that since the i-1 power - 1 of 10 must be a multiple of 9, the module 9 congruence of num and temp. If you repeat the calculation, you will get several roots, so you can know that the roots of a natural number are actually the result of module 9. Of course, there are some small details here.
Small details
We know that if it is a multiple of nine, the result of module 9 is 0, but the number root should be 9, so it needs special treatment.
code
The basic solution is included in the notes
#include<iostream>
using namespace std;
class Solution
{
public:
/// <summary>
///Simple simulation
///It is realized in two layers
///Judge whether the outer layer exceeds 1 bit
///Add the numbers in the inner layer
/// </summary>
/// <param name="num"></param>
/// <returns></returns>
/*int addDigits(int num)
{
while (num >= 10)
{
int temp = num;
num = 0;
while (temp)
{
num += temp % 10;
temp /= 10;
}
}
return num;
}*/
// I really didn't expect, tql, math
/// <summary>
///Mathematical solution
///The final result is the roots of natural numbers
///Principle, num and modulus 9 congruence
/// </summary>
/// <param name="num"></param>
/// <returns></returns>
int addDigits(int num)
{
return (num - 1) % 9 + 1;
}
};
int main(int argc, char** argv)
{
int num;
cin >> num;
Solution sol;
cout << sol.addDigits(num) << endl;
return 0;
}
3.4 subarray range and
Give you an integer array nums. In nums, the range of subarray is the difference between the largest element and the smallest element in the subarray.
Returns the sum of all subarray ranges in num.
A subarray is a sequence of consecutive non empty elements in an array.
Title Link: 2104. Subarray range and - LeetCode (LeetCode CN. Com)
Advanced
Can you design a solution with time complexity O(n)?
Analysis and thinking
It's OK not to look at the advanced level. You can directly simulate violence and continuously calculate the range of subsets. At first glance, I really didn't think of the solution of O (n).
After reading the solution, I realized that it was done with a monotonous stack. Subarray range and subarray range and LeetCode (LeetCode CN. Com)
First, we can know that the range sum is actually the sum of the difference between the maximum and minimum values of all subsets of the array. The mathematical derivation is as follows.
Mathematical derivation
a r r = ∑ ( M a x i − M i n i ) = ∑ M a x i − ∑ M i n i \begin{aligned} arr &= \sum ({Max_i - Min_i}) \\ &= \sum{Max_i} - \sum{Min_i} \end{aligned} arr=∑(Maxi−Mini)=∑Maxi−∑Mini
So how to enumerate the maximum and minimum values of all subarrays?
Assuming that the subscript of the currently enumerated number is I and the value is num [i], we can list the subscript of the first value larger than the value from the left and right, and then we can use the spacing between these subscripts and I to calculate the number of subarrays with num [i] as the maximum value, that is, the product of spacing.
The sum of all products is the sum of Maxi. Similarly, the sum of Mini can be obtained.
Then the problem comes. If you need to find the values on both sides during traversal, it obviously does not meet the time complexity of O (n), so you need to introduce monotone stack here
We use the monotonic stack to store the maximum value. Taking the minimum value as an example, when traversing the array, judge the current value and the top element of the stack and perform the operation of out of the stack until the stack is empty or the array element value corresponding to the top element is smaller than the current element value, and then put the current table into the stack. The same is true for the maximum value.
Small details
When the values are equal, it is necessary to introduce the logical size, that is, add the subscript as the judgment. Here, it is assumed that there are subscripts I and j. when the values are equal and I < j, Num [i] logic is less than num [j]
You need to traverse the array twice, that is, record the length of one-sided maximum subset with num [i] as the maximum or minimum in both directions. So we need two stacks and four arrays. In fact, the space of O (n) is still needed.
In fact, the idea of exchanging space for time is used to reduce the time complexity from n^2 to n.
code monotone stack
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
class Solution
{
public:
/// <summary>
///Monotone stack
///Use the stack to store the maximum and minimum values respectively
///The result is actually the sum of the maximum plus minus the minimum
///
/// </summary>
/// <param name="nums"></param>
/// <returns></returns>
long long subArrayRanges(vector<int>& nums)
{
int n = nums.size();
vector<int> minLeft(n), minRight(n), maxLeft(n), maxRight(n);
// Store the array subscripts corresponding to the maximum and minimum values
stack<int> minStack, maxStack;
for (int i = 0; i < n; ++i)
{
while (!minStack.empty() && nums[minStack.top()] > nums[i])
{
minStack.pop();
}
minLeft[i] = minStack.empty() ? -1 : minStack.top();
minStack.push(i);
// When < = here is actually equal, the subscript will be smaller than the current subscript, forming a logical small
while (!maxStack.empty() && nums[maxStack.top()] <= nums[i])
{
maxStack.pop();
}
maxLeft[i] = maxStack.empty() ? -1 : maxStack.top();
maxStack.push(i);
}
// Here, we should reconstruct the two monotone stacks and initialize them as empty stacks
minStack = stack<int>();
maxStack = stack<int>();
for (int i = n - 1; i >= 0; --i)
{
while (!minStack.empty() && nums[minStack.top()] >= nums[i])
{
minStack.pop();
}
minRight[i] = minStack.empty() ? n : minStack.top();
minStack.push(i);
while (!maxStack.empty() && nums[maxStack.top()] < nums[i])
{
maxStack.pop();
}
maxRight[i] = maxStack.empty() ? n : maxStack.top();
maxStack.push(i);
}
long long sumMax = 0, sumMin = 0;
for (int i = 0; i < n; i++)
{
// static_cast casts the type into the target type, which belongs to implicit type conversion
sumMax += static_cast<long long>(maxRight[i] - i) * (i - maxLeft[i]) * nums[i];
sumMin += static_cast<long long>(minRight[i] - i) * (i - minLeft[i]) * nums[i];
}
return sumMax - sumMin;
}
};
int main(int argc, char** argv)
{
int n;
cin >> n;
vector<int> nums(n);
for (int i = 0; i < n; ++i)
{
cin >> nums[i];
}
Solution sol;
cout << sol.subArrayRanges(nums) << endl;
return 0;
}
Later words
Brush it up, roll it up!