LeetCode problem solution - dynamic programming - subsequence problem
Reference: labuladong WeChat official account, hand handle brush, dynamic programming series, official account, excellent public address, recommended to everyone.
In this paper, we will pick up the routine of sub sequence problem. In fact, there are two kinds of templates. As long as we think about these two ideas, we can be sure.
Generally speaking, such questions ask you to find a longest subsequence, because the shortest subsequence is a character. There's nothing to ask. Once the subsequence and the maximum value are involved, it is almost certain that the dynamic programming technique is investigated, and the time complexity is generally O(n^2).
Since we want to use dynamic programming, we need to define dp array and find the state transition relationship. The two thought templates we talk about are the definition of dp array. Different problems may require different dp array definitions to solve.
1. The first idea template is a one-dimensional dp array:
int n = array.length;
int[] dp = new int[n];
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
dp[i] = Maximum value(dp[i], dp[j] + ...)
}
}
For example, in the longest increasing subsequence of the following example, in this idea, the definition of dp array is:
In the subarray array[0..i], the length of the target subsequence (longest increment subsequence) ending with array[i] is dp[i]
2. The second idea template is a two-dimensional dp array:
int n = arr.length;
int[][] dp = new dp[n][n];
for (int i = 0; i < n; i++) {
for (int j = 1; j < n; j++) {
if (arr[i] == arr[j])
dp[i][j] = dp[i][j] + ...
else
dp[i][j] = Maximum value(...)
}
}
This idea uses relatively more, especially involving the subsequence of two strings / arrays. In this idea, the meaning of dp array can be divided into two cases: "involving only one string" and "involving two strings".
2.1 When two strings / arrays are involved (such as the longest common subsequence), the meaning of dp array is as follows:
In the subarray arr1[0..i] and subarray arr2[0..j], we require the length of the subsequence (the longest common subsequence) to be dp[i][j].
2.2 when only one string / array is involved (such as the longest palindrome subsequence), the meaning of dp array is as follows:
In the subarray array[i..j], the length of the subsequence we require (the longest palindrome subsequence) is dp[i][j].
300. Longest increasing subsequence (medium)
Give you an integer array nums and find the length of the longest strictly increasing subsequence.
A subsequence is a sequence derived from an array. It deletes (or does not delete) the elements in the array without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].
Input: nums = [10,9,2,5,3,7,101,18] Output: 4 Explanation: the longest increasing subsequence is [2,3,7,101],Therefore, the length is 4.
Input: nums = [0,1,0,3,2,3] Output: 4
Method: dynamic programming (this is a classic problem solved by dynamic programming)
Specify the conditions in the title:
- Subsequence: no continuous subsequence is required, as long as the sequence of elements is consistent;
- Rise: the "rise" here is "strict rise". For example, subsequences such as [2, 3, 3, 6, 7] do not meet the requirements.
The question only asks the length of the longest ascending subsequence, not what the longest ascending subsequence is, so consider using dynamic programming.
-
Status definition: dp[i] indicates the length of the longest ascending subsequence ending in num [i]. That is, within the range of [0,..., I], select the length of the longest ascending subsequence that can be obtained at the end of the number num [i].
Note: ending with nums[i], it is the classic design state idea of subsequence dynamic programming problem. The idea is that there is no aftereffect of dynamic programming (the more specific the definition is, the better the derivation of state transition equation is).
-
Derivation of the state transition equation: when traversing to num [i], we should look at the dp value of the subscript interval [0,..., I - 1]. If the current number num [i] is greater than a previous number, then num [i] can be followed by this number to form a longer ascending subsequence. Look at the previous numbers, dp[i] is their maximum plus 1 1 1. That is, among those smaller than the current number, find the largest and add 1.
The state transition equation is: DP [i] = max (1 + DP [J] if J < I and num [J] < num [i]).
-
Initialization: a single number is a subsequence, and the initialization value is 1;
-
Output: This dp array should be scanned. The maximum value is the length of the longest ascending subsequence required by the topic.
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
// base case: dp arrays are all initialized to 1
Arrays.fill(dp, 1);
int res = dp[0];
for(int i = 0; i < nums.length; i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
646. Longest number pair chain (medium)
Give n number pairs. In every number pair, the first number is always smaller than the second number. Now, we define a following relationship. If and only if B < C, the number pair (c, d) can follow (a, b). We use this form to construct a number pair chain. Given a number pair set, find the length of the longest number pair chain that can be formed. You don't need to use all pairs. You can select some of them in any order.
Input:[[1,2], [2,3], [3,4]] Output: 2 Explanation: the longest number pair chain is [1,2] -> [3,4]
Solution idea: similar to the longest increasing subsequence method in the previous question, define the state dp[i] to represent the length of the longest number pair chain ending with pairs[i], and the state transition is also similar to the previous question. When I < J and pairs[i] [1] < pairs [J] [0], expand the number pair chain and update dp[j] = max(dp[j], dp[i] + 1)
Important note: this question requires that you can select a number pair in any order. In order to improve efficiency, first sort the array according to the first element from small to large;
class Solution {
public int findLongestChain(int[][] pairs) {
Arrays.sort(pairs, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0] - o2[0];
}
}); //Sort array pairs by abscissa from small to large
int m = pairs.length;
int[] dp = new int[m];
Arrays.fill(dp, 1); //base case. For each array pair, the minimum length is itself, i.e. 1
for(int i = 0; i < m; i++){
for(int j = 0; j < i; j++){
if(pairs[j][1] < pairs[i][0]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int res = 0;
for(int i = 0; i < m; i++){
res= Math.max(res, dp[i]);
}
return res;
}
}
376. Swing sequence (medium)
If the difference between consecutive numbers strictly alternates between positive and negative numbers, the number sequence is called * * swing sequence** The first difference (if any) may be positive or negative. A sequence of less than two elements is also a wobble sequence.
For example, [1,7,4,9,2,5] is a swing sequence, because the difference (6, - 3,5, - 7,3) appears alternately positive and negative. On the contrary, [1,4,7,2,5] and [1,7,4,5,5] are not swing sequences. The first sequence is because its first two differences are positive, and the second sequence is because its last difference is zero.
Given an integer sequence, returns the length of the longest subsequence of the swing sequence. The subsequence is obtained by deleting some (or no) elements from the original sequence, and the remaining elements maintain their original order.
input: [1,7,4,9,2,5] output: 6 explain: The whole sequence is a swing sequence.
input: [1,17,5,10,13,15,10,5,16,8] output: 7 explain: This sequence consists of several swing sequences with a length of 7, one of which can be[1,17,10,13,10,16,8].
Solution: whenever we choose an element as part of the swing sequence, the element is either rising or falling, depending on the size of the previous element. Then the listed status expression is:
-
up[i] indicates the length of the longest "rising swing sequence" ending with one of the previous I elements
-
down[i] indicates the length of the longest "down swing sequence" ending with one of the previous I elements.
The state transition equation is:
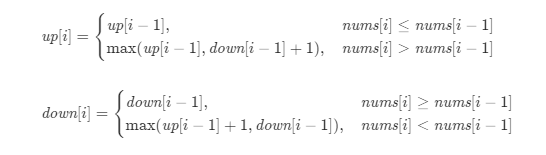
The final answer is the larger of up[n − 1] and down[n − 1], where n is the length of the sequence.
Note that in the above equation, we only need the previous state to transfer, so we can maintain two variables. In this way, we can write the following code:
up = max(up, down + 1) down = max(up + 1, down);
Note that for every downward trend from "peak" to "Valley", the down value will increase, and for every upward trend from "Valley" to "peak", the up value will increase. And the absolute value of the difference between down and up in the process is always not greater than 1, that is, up ≤ down+1 and down ≤ up+1, so max(up,down+1)=down+1 and max(up+1,down)=up+1. In this way, we can save unnecessary size comparison process.
Reference link
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
if(n <2){
return n;
}
int up = 1, down = 1;
for(int i = 1; i < n; i++){
if(nums[i] > nums[i - 1]){
up = down + 1;
}else if(nums[i] < nums[i - 1]){
down = up + 1;
}
}
return Math.max(up, down);
}
}
53. Maximum subsequence sum (simple)
Given an integer array nums, find a continuous sub array with the largest sum (the sub array contains at least one element) and return its maximum sum.
Input: nums = [-2,1,-3,4,-1,2,1,-5,4] Output: 6 Explanation: continuous subarray [4,-1,2,1] The sum of is 6.
Input: nums = [1] Output: 1
Method: dynamic programming (this is a classic problem solved by dynamic programming)
Specify the conditions in the title:
- Continuous subarray: it is required to be continuous;
-
Status definition. dp[i] indicates the "maximum sum of consecutive subarrays" ending with nums[i]. That is, within the range of [0,..., I], select the maximum sum that can be obtained by ending with the number num [i].
Under this definition, if you want to get the "maximum subarray sum" of the whole num array, you cannot directly return dp[n-1], but need to traverse the whole dp array.
-
Deduce the state transition equation: dp[i] there are two "choices", either connect with the previous adjacent subarray to form a and larger subarray; As a subarray, or not as a subarray of its own. How to choose? Since the "maximum subarray sum" is required, of course, choose the one with a larger result:
State transition equation: DP [i] = math max(nums[i], nums[i] + dp[i - 1]);.
-
initialization. A single number is a subarray, and the maximum sum value of initialization is num [0];
-
Output. This dp array should be scanned, and the maximum value is the maximum sum of successive sub arrays required by the topic.
class Solution {
public int maxSubArray(int[] nums) {
if(nums == null || nums.length == 0){
return 0;
}
int[] dp = new int[nums.length];
dp[0] = nums[0];
for(int i = 1; i < nums.length; i++){
dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
}
int res = Integer.MIN_VALUE;
for(int i = 0; i < nums.length; i++){
res = Math.max(res, dp[i]);
}
return res;
}
}
The time complexity of the above solution is O(N), and the space complexity is also O(N). It is excellent compared with the violent solution. However, note that dp[i] is only related to the state of dp[i-1], so we can carry out "state compression" to reduce the space complexity:
public int maxSubArray(int[] nums) {
if(nums == null || nums.length == 0){
return 0;
}
int pre = nums[0], res = nums[0];
for(int i = 1; i < nums.length; i++){
int cur = Math.max(nums[i], pre + nums[i]);
pre = cur;
res = Math.max(res, cur);
}
return res;
}
1143. Longest common subsequence (medium)
Given two strings text1 and text2, returns the length of the longest common subsequence of the two strings. If there is no common subsequence, 0 is returned.
The subsequence of a string refers to such a new string: it is a new string composed of the original string after deleting some characters (or not deleting any characters) without changing the relative order of characters.
- For example, "ace" is a subsequence of "abcde", but "aec" is not a subsequence of "abcde".
The common subsequence of two strings is the subsequence shared by the two strings.
Input: text1 = "abcde", text2 = "ace" Output: 3 Explanation: the longest common subsequence is "ace" ,Its length is 3.
Input: text1 = "abc", text2 = "abc" Output: 3 Explanation: the longest common subsequence is "abc" ,Its length is 3.
Solution: This is a classic topic called two-dimensional dynamic programming.
- Firstly, two concepts are distinguished: subsequences can be discontinuous; Subarray (substring) needs to be continuous;
- In addition, dynamic programming also has a routine: when dynamic programming is used for a single array or string, dynamic programming dp[i] can be defined as the result required in num [0: I]; When two arrays or strings need dynamic programming, dynamic programming can be defined as two-dimensional dp[i][j], which means the desired result obtained by matching between A[0:i] and B[0:j].
-
Status definition: for this question, you can = = define dp[i][j] to represent the longest common subsequence of text1[0:i-1] and text2[0:j-1]== For example, in the example below, dp[2][4] means that for "ac" and "babc", their LCS length is 2. The final answer we want is dp[3][6]. (Note: text1[0:i-1] refers to the 0th element to the I - 1st element of text1, which are included at both ends). The reason why dp[i][j] is not defined as text1[0:i] and text2[0:j] is to facilitate the matching between an empty string and another string when i = 0 or j = 0, so that dp[i][j] can be initialized to 0
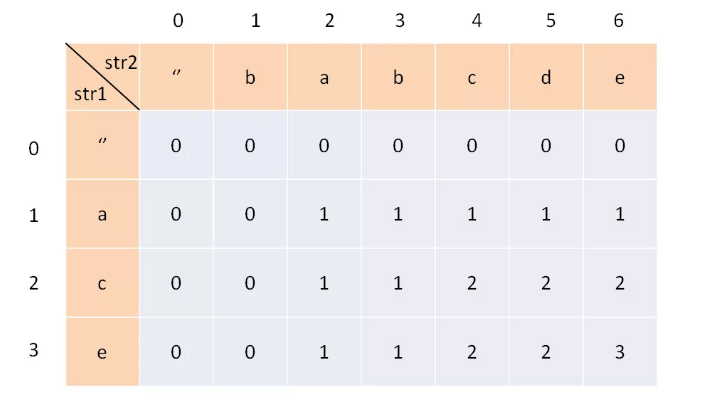
-
State transition equation:
- When text1[i - 1] == text2[j - 1], the last bit of the two substrings is equal, so the longest common subsequence is increased by 1, so dp[i][j] = dp[i - 1][j - 1] + 1;
- When text1 [I - 1]= Text2 [J - 1], indicating that the last bit of the two substrings is not equal, then the state dp[i][j] at this time should be the maximum value of dp[i - 1][j] and dp[i][j - 1].
- To sum up, the state transition equation is:
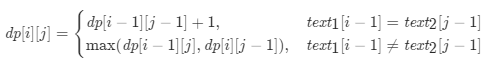
3. Initialization of status: initialization depends on the value of dp[i][j] when i = 0 and j = 0.
-
When i = 0, dp[0][j] represents the longest common subsequence of empty string and text2 in text1, and the result must be 0
-
When j = 0, dp[i][0] represents the longest common subsequence of empty string and text1 in text2, and the result must be 0
4. Traversal direction and range: because dp[i][j] depends on dp [I - 1] [J - 1], dp [I - 1] [J], dp[i][j - 1], the traversal order of I and j must be from small to large. In addition, when I and j are 0, dp[i][j] = 0, and the initialization of dp array itself is 0. Therefore, let I and j traverse directly from 1. The end of the traversal should be the length of the string len(text1) and len(text2).
5. Final returned result: because dp[i][j] means the longest common subsequence of text1[0:i-1] and text2[0:j-1]. We finally hope to find the longest common subsequence of text1 and text2. Therefore, the result to be returned is the longest common subsequence of text1 and text2 when i = len(text1) and j = len(text2). Therefore, the result to be returned is dp[len(text1)][len(text2)] when i = len(text1) and j = len(text2).
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
// Definition: the lcs length of text1[0..i-1] and text2[0..j-1] is dp[i][j]
// Target: lcs length of text1[0..m-1] and text2[0..n-1], i.e. dp[m][n]
// base case: dp[0][..] = dp[..][0] = 0
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
// Now i and j start from 1, so we need to subtract one
if(text1.charAt(i - 1) == text2.charAt(j - 1)){
// text1[i-1] and text2[j-1] must be in lcs
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[m][n];
}
}
Compared with the longest increasing subsequence, the longest common subsequence has the following differences:
- For two sequences, find their longest common subsequence.
- In the longest increasing subsequence, dp[i] represents the length of the longest increasing subsequence ending with Si, and the subsequence must contain Si; In the longest common subsequence, dp[i][j] represents the longest common subsequence length of the first I characters in S1 and the first j characters in S2, and does not necessarily include S1i and S2j.
- When seeking the final solution, dp[N][M] in the longest common subsequence is the final solution, while dp[N] in the longest increasing subsequence is not the final solution, because the longest increasing subsequence ending in SN is not necessarily the longest increasing subsequence of the whole sequence. You need to traverse the dp array to find the largest one.
583. Deletion of two strings (medium)
Given two words word1 and word2, find the minimum number of steps required to make word1 and word2 the same, and one character in any string can be deleted in each step.
input: "sea", "eat" output: 2 explain: The first step will be"sea"Become"ea",The second step will be"eat"Become"ea"
Let's calculate the minimum deletion times to make two strings the same. Then we can think about what these two strings will look like in the end?
The result of deletion is the longest common subsequence of them!
Then, to calculate the times of deletion, it can be deduced from the length of the longest common subsequence:
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int lenCommon = longestCommonSubsequence(word1, word2);
return m - lenCommon + n - lenCommon;
}
int longestCommonSubsequence(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
712. Minimum ASCII deletion and (medium) of two strings
Given the two strings S1 and S2, find the minimum sum of the ASCII values of the characters to be deleted to make the two strings equal.
input: s1 = "sea", s2 = "eat" output: 231 explain: stay "sea" Delete in "s" And will "s" Value of(115)Add the sum. stay "eat" Delete in "t" And add 116 to the sum. At the end, the two strings are equal, 115 + 116 = 231 Is the minimum sum that meets the conditions.
input: s1 = "delete", s2 = "leet" output: 403 explain: stay "delete" Delete in "dee" String becomes "let", Will be 100[d]+101[e]+101[e] Add the sum. stay "leet" Delete in "e" Will 101[e] Add the sum. At the end, both strings are equal to "let",The result is 100+101+101+101 = 403 . If you convert two strings to "lee" or "eet",We'll get 433 or 417, which is bigger than the answer.
Solution idea: the solution method of the above common subsequence is still adopted, but the value stored in the dp array in this problem is not the length of the common subsequence, but the maximum sum of their ASCII values. Finally, the minimum sum of the ASCII values of the characters to be deleted is equal to the sum of the ASCII values of the two strings minus the maximum sum of the common subsequence multiplied by 2.
class Solution {
public int minimumDeleteSum(String s1, String s2) {//Find the largest common subsequence of ascii code
int m = s1.length(), n = s2.length();
int total_sum = 0;
//Find the sum of ascii codes of two strings
for(int i = 0; i < m; i++){
total_sum += s1.charAt(i);
}
for(int j = 0; j < n; j++){
total_sum += s2.charAt(j);
}
int[][] dp = new int[m + 1][n + 1];//Adding an offset is equivalent to adding "" to the two string headers to construct a dp matrix
//Initialization matrix
for(int i = 0; i <= m; i++){
dp[i][0] = 0;
}
for(int i = 0; i <= n; i++){
dp[0][i] = 0;
}
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(s1.charAt(i - 1) == s2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1] + s1.charAt(i - 1); //Common character plus ascii
}else{
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return total_sum - 2*dp[m][n];//The minimum sum of the ASCII values of the characters to be deleted is equal to the sum of the ASCII values of the two strings minus the maximum sum of the common subsequence multiplied by 2.
}
}
72. Edit distance (difficult)
Here are two words word1 and word2. Please calculate the minimum operand used to convert word1 to word2.
You can perform the following three operations on a word:
- Insert a character
- Delete a character
- Replace one character
Input: word1 = "horse", word2 = "ros" Output: 3 Explanation: horse -> rorse (take 'h' Replace with 'r') rorse -> rose (delete 'r') rose -> ros (delete 'e')
Solution idea: to solve the dynamic programming problem of two strings, generally use two pointers I and j to point to the end of the two strings respectively, and then move forward step by step to reduce the scale of the problem.
1. Clear status: dp[i][j] represents the first I characters in word1 and the first j characters in word2. The minimum number of operations required
2. State transition: set two strings as "rad" and "apple" respectively. In order to change s1 into s2, the algorithm will do this:
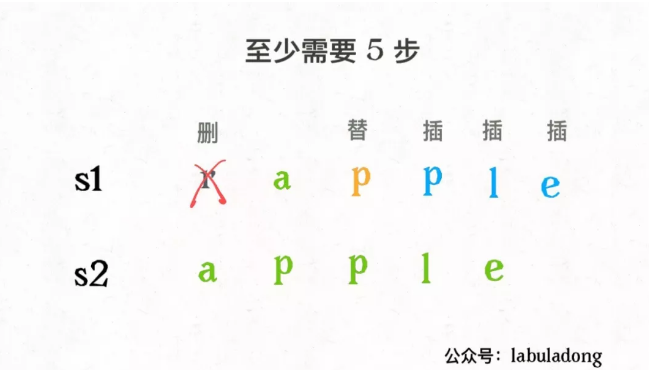
It is found that there are not only three operations, but also the fourth operation, that is, skip. For example:
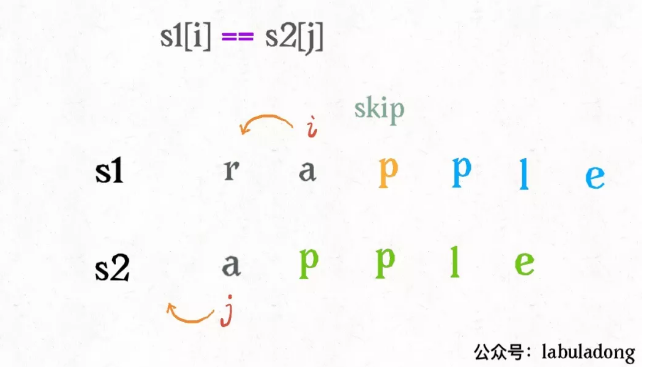
For each pair of child characters s1[i] and s2[j], there are four operations:
if s1[i] == s2[j]:
Don't do anything( skip)
i, j Move forward at the same time
else:
One out of three: # Don't forget to add one to the operand
Insert( insert) dp(i, j - 1) + 1 #1 directly insert a character like s2[j] in s1[i], then s2[j] is matched, move j forward and continue to compare with I
Delete( delete) dp(i - 1, j) + 1 #2 directly delete the character s[i], move forward I, and continue to compare with j
Replace( replace) dp(i - 1, j - 1) + 1 #3 directly replace s1[i] with s2[j], so that they match. At the same time, move forward I and j to continue the comparison
-
Base case: note that for the first row, the first column should be considered separately. We introduce '' as shown in the figure below: the first row is the minimum number of steps from word1 to word2, which is the insertion operation; The first column is that word2 is empty. The minimum number of steps required is the deletion operation. These two cases are the base case of the algorithm.
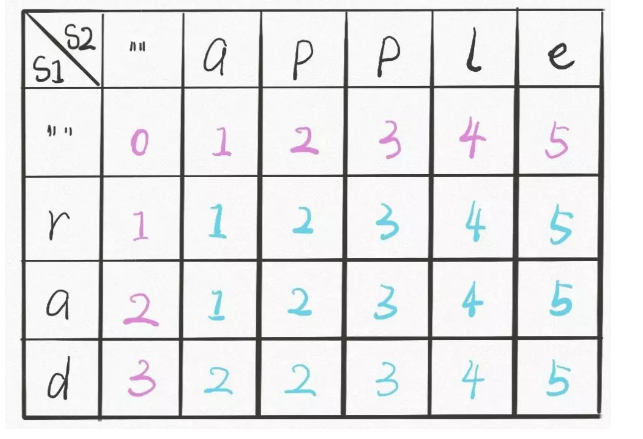
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m +1][n + 1];
//base case
for(int i = 1; i <= m; i++){
dp[i][0] = i;
}
for(int j = 1; j <= n; j++){
dp[0][j] = j;
}
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(word1.charAt(i-1) == word2.charAt(j - 1)){
dp[i][j] = dp[i -1][j - 1];
}else{
dp[i][j] = min(
dp[i - 1][j] + 1,
dp[i][j - 1] + 1,
dp[i - 1][j - 1] + 1
);
}
}
}
return dp[m][n];
}
int min(int a, int b, int c){
return Math.min(a, Math.min(b, c));
}
}
5. Longest palindrome substring (medium)
Give you a string s and find the longest palindrome substring in S.
Input: s = "babad" Output:"bab" Explanation:"aba" The same answer is in line with the meaning of the question.
Input: s = "cbbd" Output:"bb"
Solution idea: the core of solving this kind of problem is double pointer. The core idea of finding palindrome string is to judge the palindrome string by spreading from the middle to both sides. However, since the length of palindrome string may be odd or even, so
for 0 <= i < len(s):
# Find the palindrome string centered on s[i]
palindrome(s, i, i)
# Find the palindrome string centered on s[i] and s[i+1]
palindrome(s, i, i + 1)
Update answer
class Solution {
public String longestPalindrome(String s) {
//Record longest palindrome substring
String res = "";
// Enumerate palindrome strings centered on all points (one odd point and two even points)
for(int i = 0; i < s.length(); i++){
// When the palindrome string is odd, it spreads from one center point to both sides
String s1 = palindrome(s, i, i);
// When the palindrome string is even, it spreads from the two central points in the middle to both sides
String s2 = palindrome(s, i, i+1);
res = res.length() > s1.length() ? res : s1;
res = res.length() > s2.length() ? res : s2;
}
return res;
}
// Auxiliary function: find palindrome string
public String palindrome(String s, int left, int right){
// Search the palindrome string in the interval [0, s.length() - 1] to prevent the subscript from crossing the boundary
while(left >= 0 && right < s.length()){
if(s.charAt(left) == s.charAt(right)){
// When it is a palindrome string, continue to spread to both sides
left --;
right ++;
}else{
break;
}
}
// The condition at the end of the loop is s.charat (left)= s. Charat (right), so the correct interval is [left + 1, right), and the method substring(start, end) interval is [start, end], excluding end
return s.substring(left + 1, right);
}
}
So far, the problem of the longest palindrome substring has been solved, with time complexity O(N^2) and space complexity O(1).
It is worth mentioning that this problem can be solved by dynamic programming method. The time complexity is the same, but the spatial complexity must be at least O(N^2) to store DP table. This problem is a rare non optimal solution of dynamic programming.
516. Longest palindrome subsequence (medium)
Given a string s, find the longest palindrome subsequence and return the length of the sequence. It can be assumed that the maximum length of S is 1000.
Input: s = "bbbab" Output: 4 Explanation: one possible longest palindrome subsequence is "bbbb".
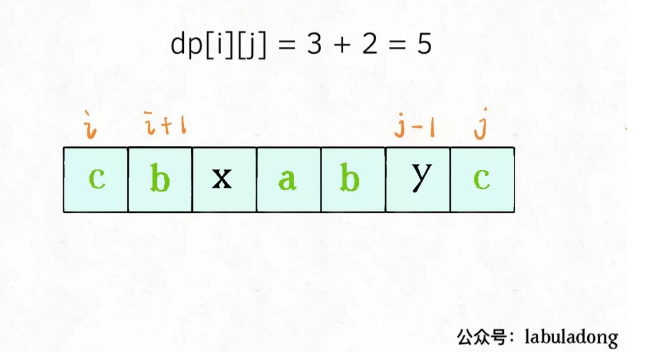
Solution: the definition of dp array in this problem is: in the substring s[i..j], the length of the longest palindrome subsequence is dp[i][j]. You must remember this definition to understand the algorithm.
Why does this problem define a two-dimensional dp array like this? Specifically, if we want to find dp[i][j], suppose you know the result of sub problem dp[i+1][j-1] (the length of the longest palindrome subsequence in s[i+1..j-1)), can you find a way to calculate the value of dp[i][j] (the length of the longest palindrome subsequence in s[i..j)?
This depends on the characters of s[i] and s[j]:
If they are equal, the longest palindrome subsequence of them plus s[i+1..j-1] is the longest palindrome subsequence of s[i..j]:
If they are not equal, it means that they cannot appear in the longest palindrome subsequence of s[i..j], then add them to s[i+1..j-1] respectively to see which substring produces a longer palindrome subsequence:
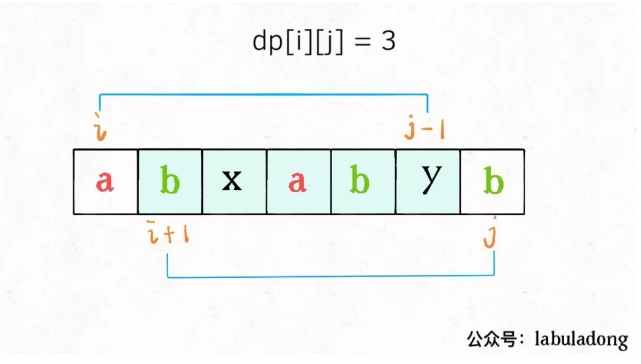
The above two cases are written in code as follows:
if (s[i] == s[j])
// They must be in the longest palindrome subsequence
dp[i][j] = dp[i + 1][j - 1] + 2;
else
// s[i+1..j] and s[i..j-1] whose palindrome subsequence is longer?
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
First, clarify the base case. If there is only one character, it is obvious that the length of the longest palindrome subsequence is 1, that is, dp[i][j] = 1,(i == j).
Because i must be less than or equal to j, there is no subsequence for those positions where i > J and should be initialized to 0.
In addition, look at the state transition equation just written. If you want to find dp[i][j], you need to know the three positions dp[i+1][j-1], dp[i+1][j], dp[i][j-1]; Take another look at the base case we determined. After filling in the dp array, it is as follows:
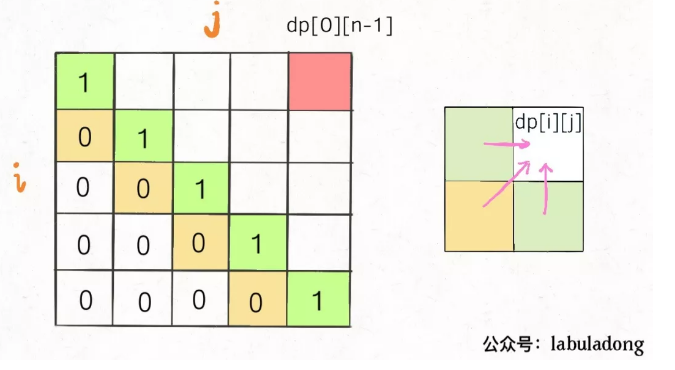
In order to ensure that the positions in the left, lower and lower left directions have been calculated for each calculation dp[i][j], you can only traverse obliquely or reversely:
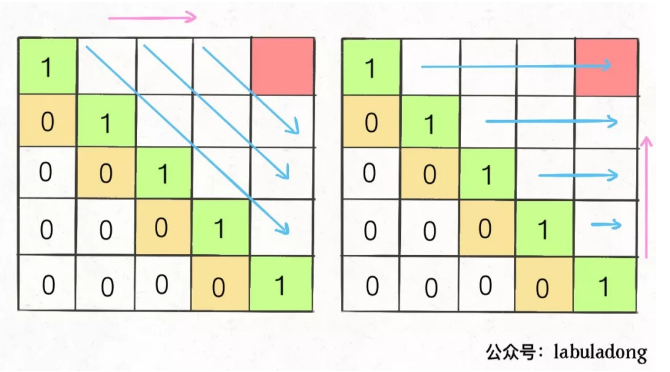
I choose reverse traversal. The code is as follows:
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for(int i = 0; i < n; i++){
dp[i][i] = 1;
}
for(int i = n - 1; i >= 0; i--){
for(int j = i + 1; j < n; j++){
// State transition equation
if(s.charAt(i) == s.charAt(j)){
dp[i][j] = dp[i + 1][j - 1] + 2;
}else{
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
return dp[0][n - 1]; //The length of the longest palindrome substring of the whole s
}
}