1. The longest chain that a number pair can form
646. Longest number pair chain (Medium)
Method 1: greedy algorithm
Sort all pairs according to the size of the second number. The first step is to select the pair with the smallest ending number. Then, each step selects the number that does not conflict with the last selected number pair and has the smallest ending number.
class Solution:
def findLongestChain(self, pairs: List[List[int]]) -> int:
pairs.sort(key=lambda x: (x[1], x[0]))
res = 1
tail = pairs[0][1]
for _, item in enumerate(pairs):
if item[0] > tail:
tail = item[1]
res += 1
return res
Method 2: dynamic programming
Sort all the first numbers according to their sizes. The subproblem is the longest chain with pairs[i] (i=1, 2, 3... N) as the end point. a[i] indicates the chain length with pairs[i] as the end point.
- Initial state: a[i] = 1
- A [i] = max {a [i], a [J] + 1} 0 < = J < I and pairs [i] [0] > pairs [J] [1]
Find the maximum value of [i].
class Solution:
def findLongestChain(self, pairs: List[List[int]]) -> int:
pairs.sort()
dp = [1] * len(pairs)
for i in range(len(pairs)):
for j in range(i):
if pairs[i][0] > pairs[j][1]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
2. Distribute biscuits
455. Distribution of biscuits (Easy)
Method: sorting + greed
In order not to waste biscuits, each child should be allocated the smallest biscuit that can satisfy the child.
class Solution:
def findContentChildren(self, g: List[int], s: List[int]) -> int:
g.sort()
s.sort()
i = j = res = 0
len_g, len_s = len(g), len(s)
while i < len_g and j < len_s:
if s[j] >= g[i]:
res += 1
i += 1
j += 1
return res
3. Number of non overlapping intervals
435. Non overlapping interval (Medium)
Greedy thinking, calculate the maximum number of non overlapping intervals, and then subtract the number of non overlapping intervals from the total number of intervals. Sort the interval according to the ending number. The smaller the ending is, the more space is left for the following interval. Each time, choose the interval with the smallest ending and no overlap with the front.
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
intervals.sort(key=lambda x:(x[1], x[0]))
tail = intervals[0][1]
res = 1
for _, item in enumerate(intervals):
if item[0] >= tail:
res += 1
tail = item[1]
return len(intervals)-res
4. How many darts do you need to pierce the balloon
452. Detonate the balloon (Medium) with the minimum number of arrows
Method: sorting + greed
Here is to calculate the total number of non overlapping intervals, sort according to the end coordinates of each interval, select the first interval, and then select the interval that does not overlap with the current interval and has the smallest end coordinates each time.
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
points.sort(key=lambda x:(x[1], x[0]))
tail = points[0][1]
res = 1
for _, item in enumerate(points):
if item[0] > tail:
tail = item[1]
res += 1
return res
5. Reorder by height serial number
406. Reconstruct the queue according to height (Medium)
Sort according to the descending order of height, and sort according to the ascending order of sequence number if the height is equal. Traverse all people and insert each person into the corresponding position.
When placing the i-th person:
- The 0,..., i − 1 person has been arranged in the queue. As long as they stand in front of the i person, they will have an impact on the i person, because they are higher than the i person;
- The i+1,..., n − 1 person has not been put into the queue, and no matter where they stand, they have no effect on the i-th person, because they are shorter than the i-th person.
Since the person behind will not affect the i-th person, we can use the method of inserting empty space. When we put the i-th person into the queue, we can insert it into the queue so that there is ki person in front of him
Examples: [5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
Sort:
[7, 0] [7, 1] [6, 1] [5, 0] [5, 2] [4, 4]
Insert:
[7, 0]
[7, 0] [7, 1]
[7, 0] [6, 1] [7, 1]
[5, 0] [7, 0] [6, 1] [7, 1]
[5, 0] [7, 0] 5, 2] [6, 1] [7, 1]
[5, 0] [7, 0] 5, 2] [6, 1] [4, 4] [7, 1]
class Solution:
def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
people.sort(key=lambda x: (-x[0], x[1]))
ans = list()
for item in people:
if len(ans) <= item[1]:
ans.append(item)
else:
ans.insert(item[1], item)
return ans
The following writing method can also achieve the insertion effect
class Solution:
def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
people.sort(key=lambda x: (-x[0], x[1]))
ans = list()
for item in people:
ans[item[1]:item[1]] = [item]
return ans
6. The biggest gain from buying and selling stocks
121. The best time to buy and sell stocks (Easy)
Record the previous minimum price. Take this price as the buying price and the current price as the selling price. The current profit is greater than the previous profit. Update the profit.
class Solution:
def maxProfit(self, prices: List[int]) -> int:
small_price = prices[0]
res = 0
for _, item in enumerate(prices):
small_price = min(small_price, item)
res = max(res, item-small_price)
return res
7. Maximum return on buying and selling stocks II
122. The best time to buy and sell stocks II(Medium)
As long as the price is increasing, there will be benefits.
For [a, b, c, d], if there is a < = B < = C < = D, the maximum return is d - a. And d - a = (d - c) + (c - b) + (b - a). Therefore, when a price [i] is accessed and price [i] - price [I-1] > 0, then prices[i] - prices[i-1] is added to the income.
class Solution:
def maxProfit(self, prices: List[int]) -> int:
res = 0
n = len(prices)
for i in range(1, n):
if prices[i] > prices[i-1]:
res += prices[i] - prices[i-1]
return res
8. Plant flowers
605. Flower planting (Easy)
First, change the array to [1,0] + flowerbed + [0,1], so there is no need to consider the ending problem
If the subscripts I and j have flowers and there is an open space between them, there can be (j-i-2)//2 flowers between them. Maintenance pre_flower indicates the subscript position of the last planted flower. Traverse the array flowerbed from left to right. When flowerbed[i]=1 is encountered, according to pre_ The values of flower and I calculate the maximum number of flowers that can be planted in the previous interval, and update pre_flower. Finally, judge whether the maximum number of flowers that can be planted in the whole flower bed is greater than or equal to n.
In the cycle, when the flowers that can be planted are greater than or equal to n, they can jump out of the cycle directly.
class Solution:
def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:
flowerbed.insert(0, 0)
flowerbed.insert(0, 1)
flowerbed.append(0)
flowerbed.append(1)
pre_flower, res = 0, 0
for i, item in enumerate(flowerbed):
if i > 0 and item:
res += (i-pre_flower-2)//2
if res >= n:
return True
pre_flower = i
return res >= n
9. Determine whether it is a string
392. Judgment subsequence (Easy)
Methods: Double finger acupuncture
Initialize the two subscripts i and j, pointing to the initial positions of s and t, respectively. If the matching is successful, it will move to the right at the same time. If the matching fails, J will move to the right and i will remain unchanged.
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
s_len = len(s)
t_len = len(t)
i, j = 0, 0
while i < s_len and j < t_len:
if s[i] == t[j]:
i += 1
j += 1
return i >= s_len
10. Modify a number to become a non decreasing group
665. Non decreasing column (Medium)
Traverse the array. If decrement is encountered:
It can also be modified:
Modify scheme 1: reduce num [i] to num [i + 1];
Modification scheme 2: enlarge num [i + 1] to num [i];
Cannot be modified: return false directly;
class Solution:
def checkPossibility(self, nums: List[int]) -> bool:
n = len(nums)
if n <=1: return True
flag = True if nums[0] <= nums[1] else False
for i in range(1, n-1):
if nums[i] > nums[i+1]:
if flag:
flag = False
if nums[i+1] >= nums[i-1]:
nums[i] = nums[i+1]
else:
nums[i+1] = nums[i]
else:
return flag
return True
11. Maximum sum of continuous subarrays
53. Maximum subarray sum (Easy)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
res, cur = nums[0], 0
n = len(nums)
for _, item in enumerate(nums):
cur += item
res = max(res, cur)6785
cur = cur if cur > 0 else 0
return res
12. Separating strings brings the same characters together
763. Divide the letter interval (Medium)
First, the position of the last occurrence of each character in the string is counted. Traverse each character of the string from front to back, and check the position of the last occurrence of these characters. When the current position is equal to the position of the last occurrence of the previous characters, it means that the previous characters will not appear in the following characters. You can separate the character string here.
class Solution:
def partitionLabels(self, s: str) -> List[int]:
last = [0] * 26
for i, c in enumerate(s):
last[ord(c) - ord('a')] = i
begin, end = 0, 0
res = []
for i, c in enumerate(s):
end = max(end, last[ord(c) - ord('a')])
if end == i:
res.append(i - begin + 1)
begin = i + 1
return res
13. Minimum difference II
910. Minimum difference II(Medium)
Let's put the original array in order first. However, the topic requires each element to move K up or down, and then requires the "maximum and minimum distance" of the new array to be as small as possible. Split the array into two halves, move the left half up and the right half down, as shown in the figure below. Black is the original array and red is the new array:
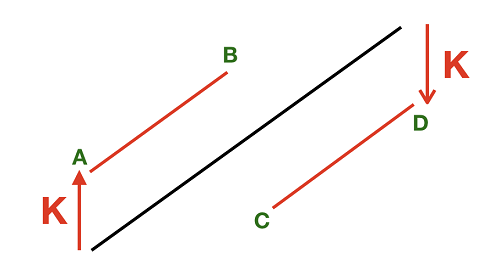
When dividing the array at I, the elements of A[0] ~ A[i] move up, and the elements of A[i + 1] ~ A[A.length - 1] move down.
At this time, the value of point B is A[i] + K, and the value of point D is A[A.length - 1] - K.
The maximum value of the new array is either point B or point D, that is, the maximum value of the new array is Max(A[i] + K, A[A.length - 1] - K).
Similarly, the value of point A is A[0] + K, and the value of point C is A[i + 1] - K.
The minimum value of the new array is either point A or point C, that is, the minimum value of the new array is Min(A[0] + K, A[i + 1] - K).
The "difference between the maximum and minimum values of the new array" required by the topic is Max(A[i] + K, A[A.length - 1] - K) - Min(A[0] + K, A[i + 1] - K). Let I traverse from 0 to A.length - 2 one by one, and take the minimum value of the above formula.
class Solution(object):
def smallestRangeII(self, A, K):
len_A = len(A)
A = sorted(A)
res = A[len_A-1] - A[0]
for i in range(0, len_A-1):
max_num = max(A[i]+K, A[len_A-1]-K)
min_num = min(A[0]+K, A[i+1]-K)
res = min(res, max_num-min_num)
return res
14. Swing sequence
When there is a continuous increase (or decrease) in the sequence, in order to form the pendulum sequence, we only need to retain the first element of the continuous increase (or decrease), which is more likely to make the latter element of the tail become the next element of the pendulum sequence.
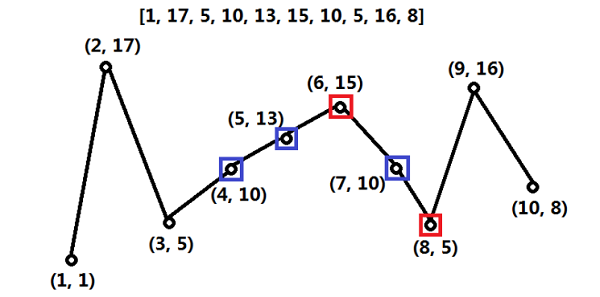
class Solution(object):
def wiggleMaxLength(self, nums):
len_num = len(nums)
if len_num <= 1:
return len_num
pre_diff = nums[1] - nums[0]
res = 1 if pre_diff == 0 else 2
for i in range(2, len_num):
diff = nums[i] - nums[i-1]
if (diff < 0 and pre_diff >= 0) or (diff > 0 and pre_diff <= 0):
res += 1
pre_diff = diff
return res
Time complexity: O(n)
Space complexity: O(1)