1. Title

Give you a head node of the linked list to judge whether there are links in the linked list.

If there is a node in the linked list that can be reached again by continuously tracking the next pointer, there is a ring in the linked list. In order to represent the rings in a given linked list, the evaluation system uses the integer pos to represent the position where the tail of the linked list is connected to the linked list (the index from 0 0 0). If pos is − 1 -1 − 1, there is no ring in the linked list. Note: pos is not passed as a parameter, but only to identify the actual situation of the linked list.

Returns true if there are links in the linked list. Otherwise, false is returned.

1.1 example

• Example 1 1 1 :

• Input: head = [3, 2, 0, -4], pos = 1;
• Output: true;
• Explanation: there is a ring in the linked list, and its tail is connected to the second node.

• Example 2 2 2 :

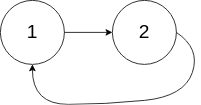
• Input: head = [1, 2], pos = 0;
• Output: true;
• Explanation: there is a ring in the linked list, and its tail is connected to the first node.

• Example 3 3 3 :

• Input: head = [1], pos = -1;
• Output: [0];
• Explanation: there are no links in the linked list.

1.2 description

• Source: LeetCode
• Link: https://leetcode-cn.com/problems/linked-list-cycle

1.3 restrictions

• − 1 0 5 ≤ Node.val ≤ 1 0 5 -10^5 \le \text{Node.val} \le 10^5 −105≤Node.val≤105 ；
• The number range of nodes in the linked list is [ 0 , 1 0 4 ] [0, 10^4] [0,104] ；
• pos is - 1 or a valid index in the linked list.

1.4 advanced

Can you solve this problem with O(1), which is constant memory?

2. Solution I

2.1 analysis

For this problem, the simplest and direct way is to traverse the given linked list, use a list to save the traversed nodes, and judge whether its next field points to a node saved in the list before saving the current node. If so, return True. If such a node is not found until all nodes are traversed, Returns False.

2.2 answers

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None


class Solution:
    def has_cycle(self, head: ListNode) -> bool:
        nodes = []
        cursor = head
        while cursor:
            if cursor in nodes:
                return True
            nodes.append(cursor)
            cursor = cursor.next
        return False


def main():
    node4 = ListNode(-4)
    node3 = ListNode(0)
    node2 = ListNode(2)
    node1 = ListNode(3)
    node1.next, node2.next, node3.next, node4.next = node2, node3, node4, node2
    head = node1
    sln = Solution()
    print(sln.has_cycle(head))  # True


if __name__ == '__main__':
    main()

In fact, changing the above auxiliary storage structure for storing traversal nodes from list to set can improve some time complexity.

2.3 complexity

• Time complexity: O ( n ) O(n) O(n) ；
• Space complexity: O ( n ) O(n) O(n) .

3. Solution II

3.1 analysis

In fact, although pos mentioned in the title has little to do with problem solving, it can be used to give a space complexity of O ( 1 ) O(1) Solution of O(1).

For the linked list given by the topic, there are only two cases:

• The linked list forms a ring. At this time, if you continue to traverse along the next field of the node, you will fall into an infinite loop;
• The linked list does not form a ring. At this time, if you continue to traverse along the next field of the node, the cycle will naturally terminate.

Therefore, as long as we do some special treatment for the link of the linked list.

Specifically, when the linked list forms a ring, as long as an instance attribute is set for each node during the first cycle of traversal, in fact, any instance attribute can be set. Here, for convenience, it is set as the index pos of this node. In this way, judge whether the node has this attribute during the second round of traversal. If so, it indicates that the node with the pos attribute set before is traversed because the linked list is in a ring, so it directly returns True.

It should be noted that in Python, the function setattr can be used to set a non-existent attribute on an object, and the function hasattr can be used to judge whether an object has an attribute.

3.2 answers

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None


class Solution:
    def efficient_has_cycle(self, head: ListNode) -> bool:
        cursor = head
        i = 0
        while cursor:
            if hasattr(cursor, 'pos'):
                return True
            setattr(cursor, 'pos', i)
            cursor = cursor.next
            i += 1
        return False


def main():
    node4 = ListNode(-4)
    node3 = ListNode(0)
    node2 = ListNode(2)
    node1 = ListNode(3)
    node1.next, node2.next, node3.next, node4.next = node2, node3, node4, node2
    head = node1
    sln = Solution()
    print(sln.efficient_has_cycle(head))  # True


if __name__ == '__main__':
    main()

3.3 complexity

• Time complexity: O ( n ) O(n) O(n) ；
• Space complexity: O ( 1 ) O(1) O(1) .

4. Solution III

4.1 analysis

Author: LeetCode-Solution

This method requires readers to understand the "Floyd circle judgment algorithm" (also known as the tortoise rabbit race algorithm). Suppose "Tortoise" and "rabbit" move on the linked list, "rabbit" runs fast and "Tortoise" runs slowly.

When tortoise and rabbit start moving from the same node on the linked list:

1. If there is no link in the list, the "rabbit" will always be in front of the "Tortoise";
2. If there is a ring in the list, the rabbit will enter the ring before the tortoise and move in the ring all the time. When the tortoise enters the ring, due to the fast speed of the rabbit, it will meet the tortoise at some time, that is, it sets several circles of the tortoise.

Therefore, we can solve this problem according to the above ideas. Specifically, two pointers are defined, one fast and one slow. The slow pointer moves only one step at a time, while the fast pointer moves two steps at a time.

Initially, the slow pointer is at position head and the fast pointer is at position head.next. In this way, if the fast pointer catches up with the slow pointer in the process of moving, it means that the linked list is a ring linked list. Otherwise, the fast pointer will reach the end of the linked list, which is not a ring linked list.

4.2 answers

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None


class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        if not head or not head.next:
            return False

        slow = head
        fast = head.next

        while slow != fast:
            if not fast or not fast.next:
                return False
            slow = slow.next
            fast = fast.next.next

        return True


def main():
    node4 = ListNode(-4)
    node3 = ListNode(0)
    node2 = ListNode(2)
    node1 = ListNode(3)
    node1.next, node2.next, node3.next, node4.next = node2, node3, node4, node2
    head = node1
    sln = Solution()
    print(sln.hasCycle(head))  # True


if __name__ == '__main__':
    main()

4.3 complexity

• Time complexity: O ( n ) O(n) O(n), where n n n is the number of nodes in the linked list.
  • When there is no ring in the linked list, the fast pointer will reach the tail of the linked list before the slow pointer, and each node in the linked list will be accessed twice at most;
  • When there are links in the linked list, the distance between the fast and slow pointers will be reduced by one after each round of movement. The initial distance is the length of the ring, so it can move at most n n n rounds (in doubt here).
• Space complexity: O ( 1 ) O(1) O(1) . Only the extra space of two pointers is used.