title from LeetCode, link: combination-sum . The specific description is: given an array of candidates without repeating elements and a target number target, find out all combinations in candidates that can make the number and target. The numbers in candidates can be selected repeatedly without limit.
Explain:

• All numbers, including target, are positive integers.
• A solution set cannot contain duplicate combinations.

Example 1:

Input: candidates = [2,3,6,7], target = 7,
The solution set is:
[
  [7],
  [2,2,3]
]

Example 2:

Input: candidates = [2,3,5], target = 8,
The solution set is:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

  the whole search process can be seen as the process of generating a search tree. The root node is the sum of 0. Suppose candidates have L candidates, then L nodes will be generated from the root node. The sum of each node is 0 + candidates. Because it can be repeated infinite times, L nodes can always be regenerated from each node down. At the same time, considering that the number of candidates is greater than zero, when a node gets a sum greater than or equal to 0, it can stop. If it is equal to 0, backtracking to the root node will get a qualified combination. This is the backtracking algorithm, which can also be regarded as a depth first traversal. At the same time, candidates can be sorted first to facilitate pruning in time. That is, when generating L sub nodes for a node, it is found that the sum of the current generated sub nodes is greater than or equal to 0, then the subsequent sub nodes (and must be greater than 0) can be directly discarded.

  JAVA version code is as follows:

class Solution {
    private void recursion(int[] candidates, int start, int target, List<Integer> oneSolution, List<List<Integer>> result) {
        for (int i = start; i < candidates.length; ++i) {
            if (candidates[i] == target) {
                List<Integer> temp = new LinkedList<>(oneSolution);
                temp.add(candidates[i]);
                result.add(temp);
            }
            else if (candidates[i] < target) {
                List<Integer> temp = new LinkedList<>(oneSolution);
                temp.add(candidates[i]);
                recursion(candidates, i, target - candidates[i], temp, result);
            }
            else {
                break;
            }
        }
    }

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int L = candidates.length;
        List<List<Integer>> result = new LinkedList<>();    
        Arrays.sort(candidates);
        recursion(candidates, 0, target, new LinkedList<Integer>(), result);
        return result;
    }
}

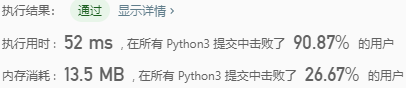
  the results submitted are as follows:

The Python code is as follows:

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        L = len(candidates)
        def recursion(candidates, start, target, oneSolution, result):
            for i in range(start, L):
                if candidates[i] == target:     #The current number is equal to target. A set of matching
                    temp = oneSolution.copy()
                    temp.append(candidates[i])
                    result.append(temp)
                elif candidates[i] < target:    #If the current number is less than target, you can add the combination to be selected to see if the number to be added can meet the conditions
                    temp = oneSolution.copy()
                    temp.append(candidates[i])
                    recursion(candidates, i, target - candidates[i], temp, result)
                else:                           #The current number is greater than target. There must be no qualified ones. Jump out directly
                    break

        candidates.sort()
        result = []
        recursion(candidates, 0, target, [], result)
        return result

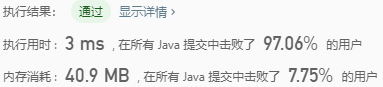
  the results submitted are as follows: