1. Title Description

Give you an integer array nums. In nums, the range of subarray is the difference between the largest element and the smallest element in the subarray.
Returns the sum of all subarray ranges in num.
A subarray is a sequence of consecutive non empty elements in an array.

Example 1:
Input: num = [1,2,3]
Output: 4
Explanation: the six subarrays of nums are as follows:
[1] , range = max min = 1 - 1 = 0
[2] , range = 2 - 2 = 0
[3] , range = 3 - 3 = 0
[1,2], range = 2 - 1 = 1
[2,3], range = 3 - 2 = 1
[1,2,3], range = 3 - 1 = 2
The sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4
Example 2:

Input: num = [1,3,3]
Output: 4
Explanation: the six subarrays of nums are as follows:
[1] , range = max min = 1 - 1 = 0
[3] , range = 3 - 3 = 0
[3] , range = 3 - 3 = 0
[1,3], range = 3 - 1 = 2
[3,3], range = 3 - 3 = 0
[1,3,3], range = 3 - 1 = 2
The sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4
Example 3:

Input: num = [4, - 2, - 3,4,1]
Output: 59
Explanation: the sum of all subarray ranges in num is 59
 
Tips:

• 1 <= nums.length <= 1000
• -10^9 <= nums[i] <= 10^9

Advanced: can you design a solution with time complexity of O(n)?

Source: LeetCode
Link: https://leetcode-cn.com/problems/sum-of-subarray-ranges
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

2. Problem solving analysis

2.1 solution 1

Scan all possible subarrays directly, calculate the maximum and minimum values of each subarray, and add them to the sum after calculating their difference.

Note that instead of scanning all subsets, the subarray must be continuous. Total number of subsets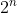, and how many subarrays are there? There are n subarrays of length 1, n-1 subarrays of length 2, and 1 subarray of length N, a total of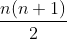And it's obvious that a subarray with a length of 1 can be ignored.

The scanning is divided into two layers. The outer layer is the length of the scanning sub array, from 2 to n; The starting position of the inner sublayer corresponding to the scanning length of the array.

See subArrayRanges1() for code

[complexity analysis]
Time complexity: O(n^3), where n is the size of the array. The two-level cycle requires O(n^2), and the time required for each sub array to find the maximum and minimum values also depends on N, so the total time complexity should be O(n^3) (not very confident, to be further confirmed)
Space complexity: O(1)

2.2 solution 2

Solution 1 submitted negative judgment, exceeding the time limit.

The maximum and minimum values of subarray in solution 1 are obtained independently by lattice, and there are many redundancies.

Consider all subarrays with length greater than 1 with num [0:2], Num [0:3],..., with num [0] as the left boundary,  nums[0:n]. Consider the maximum and minimum values of nums[0:k] and nums[0:k+1]. If the maximum and minimum values of nums[0:k] have been obtained, maxVal and minVal respectively, the maximum and minimum values of nums[0:k+1] do not need to be found from scratch, but only need to use nums[k] to compare maxVal and minVal respectively.

In this way, the maximum and minimum values of all subarrays with num [0] as the left boundary can be obtained in an iterative way

The cost of finding the maximum and minimum of each subarray is constant time complexity. Therefore, the total time complexity will be reduced to O(n^2)

See subArrayRanges2() for code

3. Code implementation

import time
import random
from typing import List

class Solution:
    def subArrayRanges1(self, nums: List[int]) -> int:
        # Time limit exceeded
        maxsum = 0
        for k in range(2,len(nums)+1):
            for m in range(len(nums)-k+1):
                # print(k,m)
                maxsum += max(nums[m:m+k]) - min(nums[m:m+k])
        return maxsum

    def subArrayRanges2(self, nums: List[int]) -> int:
        ans, n = 0, len(nums)
        for i in range(n):
            minVal, maxVal = float('inf'), -float('inf')
            for j in range(i, n):
                minVal = min(minVal, nums[j])
                maxVal = max(maxVal, nums[j])
                ans += maxVal - minVal
        return ans

if __name__ == '__main__':        
    
    sln = Solution()  

    # nums = [1,2,3]
    # tStart = time.time()        
    # ans = sln.subArrayRanges1(nums)
    # tElapsed = time.time() - tStart            
    # print('input={0}, ans={1}, tCost={2:3.2f}(sec)'.format(nums,ans,tElapsed))        

    # nums = [1,3,3]
    # tStart = time.time()        
    # ans = sln.subArrayRanges1(nums)
    # tElapsed = time.time() - tStart            
    # print('input={0}, ans={1}, tCost={2:3.2f}(sec)'.format(nums,ans,tElapsed))        
    
    # nums = [4,-2,-3,4,1]
    # tStart = time.time()        
    # ans = sln.subArrayRanges1(nums)
    # tElapsed = time.time() - tStart            
    # print('input={0}, ans={1}, tCost={2:3.2f}(sec)'.format(nums,ans,tElapsed))            
    
    nums = [random.randint(-10**9, 10**9) for k in range(1000)]
    tStart = time.time()        
    ans = sln.subArrayRanges1(nums)
    tElapsed = time.time() - tStart            
    print('input={0}, ans={1}, tCost={2:3.2f}(sec)'.format(nums,ans,tElapsed))                
    
    nums = [random.randint(-10**9, 10**9) for k in range(1000)]
    tStart = time.time()        
    ans = sln.subArrayRanges2(nums)
    tElapsed = time.time() - tStart            
    print('input={0}, ans={1}, tCost={2:3.2f}(sec)'.format(nums,ans,tElapsed))      

The above solution 2 is also the time complexity of O(n^2), but how to design a solution with time complexity of O(n)?

General catalogue of this series: Leetcode problem solving notes of slow ploughing of stupid cattle (dynamic update...)https://chenxiaoyuan.blog.csdn.net/article/details/123040889