catalogue

1. Title Description

2. Problem solving analysis

2.1 solution 1: two dimensional matrix simulation

2.2 solution 2: directly calculate the address

3. Code implementation

1. Title Description

A given string s is arranged in a Z-shape from top to bottom and from left to right according to the given number of lines numRows.
For example, when the input string is "paypalishing" and the number of lines is 3, the arrangement is as follows:

P   A   H   N
A P L S I I G
Y   I   R
After that, your output needs to be read line by line from left to right to produce a new string, such as "PAHNAPLSIIGYIR".
Please implement this function to transform the string to the specified number of lines:
string convert(string s, int numRows);
 

Example 1:
Enter: S = "paypalishing", NumRows = 3
Output: "PAHNAPLSIIGYIR"

Example 2:
Enter: S = "paypalishing", NumRows = 4
Output: "PINALSIGYAHRPI"
Explanation:
P     I    N
A   L S  I G
Y A   H R
P     I

Example 3:
Input: s = "A", numRows = 1
Output: "A"

Tips:
1 <= s.length <= 1000
s consists of English letters (lowercase and uppercase), ',' and '.' form
1 <= numRows <= 1000

Source: LeetCode
Link: https://leetcode-cn.com/problems/zigzag-conversion
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

2. Problem solving analysis

2.1 solution 1: two dimensional matrix simulation

Of course, the most intuitive way is to directly simulate with a two-dimensional matrix. Write the original string into the two-dimensional matrix according to the problem setting rules, and then read it out according to the row. Of course, because it is written in Z-shape, there are many places where elements are not written, so it needs to be skipped when reading.

2.2 solution 2: directly calculate the address

Due to the arrangement rules (including writing and writing), there is a fixed one-to-one mapping relationship between the output character sequence number and the input character sequence number under the condition that n is known. Based on this mapping relationship, the output string can be extracted from the input string according to the output order to form the output string.

Take n=4 as an example, the serial number of the input character written into the two-dimensional matrix is shown in the figure below (note that this example is written by row, that is, it is transposed with the problem design requirements, and then read by column to get the same result):

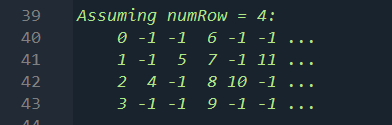
It can be seen that every six numbers constitute a writing cycle (6=2*n-2), so the data of the first line of output is to extract one character every six characters in sequence from the serial number 0 in the original string. The data in the last line is also extracted from the original string every 6 characters in order, just starting from the character of serial number 3.

However, the rules of the middle line are different from those of the first and last lines. These middle rows have only two characters in each cycle (every three columns or (n-1) columns form a cycle). As shown in the figure above, in the first cycle of line 2 (row_idx=1), the first is sequence number 1(row_idx), and the second is sequence number 5(row_idx+n+2-2*row_idx); In the first cycle of line 3 (row_idx=2), the first is sequence number 2(row_idx), and the second is sequence number 4(row_idx+n+2-2*row_idx)... Taking the number of cycles (col_idx//n) into account, we can get the law of the character sequence number read in each line with respect to n. See the following for details, which will not be repeated here.

3. Code implementation

class Solution:
    def convert(self, s: str, numRows: int) -> str:
        if numRows <= 1 or numRows >= len(s):
            return s

        rslt = []
        for r in range(numRows):        
            k = r        
            if r == 0:                  # The first line
                step = 2 * numRows - 2
                while k < len(s): 
                    rslt.append(s[k])
                    k = k + step
            elif r <= numRows-2:        # The middle lines
                step2 = 2 * r
                step1 = 2 * numRows - 2 - step2
    
                cnt = 0
                while k < len(s):
                    rslt.append(s[k])
                    if (cnt%2) == 0:
                        step = step1
                    else:
                        step = step2
                    k = k + step                
                    cnt = cnt + 1
            else:                       # The last line
                step = 2 * numRows - 2
                while k < len(s):
                    rslt.append(s[k])
                    k = k + step
        #print(s, ' --> ', rslt)
        #print(len(s), len(rslt))    
        assert(len(s) == len(rslt))
        return ''.join(rslt)

if __name__ == '__main__':

    sln   = Solution()

    # Testcase0
    print('Testcase0...')
    s = "PAYPALISHIRING"
    numRows = 3
    print(s, ' --> ', sln.convert(s, numRows))

    # Testcase1
    print('Testcase1...')
    s = "PAYPALISHIRING"
    numRows = 4
    print(s, ' --> ', sln.convert(s, numRows))
    
    # Testcase2
    print('Testcase2...')
    s = "HELLO"
    numRows = 1
    print(s, ' --> ', sln.convert(s, numRows))

    # Testcase4
    print('Testcase3...')
    s = "HELLO"
    numRows = 5
    print(s, ' --> ', sln.convert(s, numRows))

    # Testcase4
    print('Testcase4...')
    s = "HELLO"
    numRows = 0
    print(s, ' --> ', sln.convert(s, numRows))

General catalogue of this series: Leetcode problem solving notes of slow ploughing of stupid cattle (dynamic update...)https://chenxiaoyuan.blog.csdn.net/article/details/123040889