Title Description:

Given a tree with n nodes (node values 1~n), the graph after adding an edge to the tree. The two vertices of the added edge are contained between 1 and N ， and the additional edge does not belong to the existing edge in the tree. The information of the graph is recorded in the two-dimensional array edges with length n. edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.

Please find an edge that can be deleted. After deletion, the remaining part can be a tree with n nodes. If there are multiple answers, the last edge in the array "edges" is returned.

Original title reference link: https://leetcode-cn.com/problems/7LpjUW

analysis:

In short, the default given in this question is a graph containing a separate closed loop. You only need to locate the edge that appears on the closed loop for the first time in the reverse order of the input edges to restore the graph to a tree.

Example 1:

1 input: edges = [[1,2],[1,3],[2,3]]
2 output: [2,3]

Example 2:

 

 

 

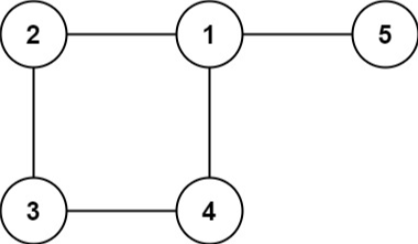
1 input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
2 output: [1,4]

Cpp solution 1 - recursive edge Division:

search_ one_ The pair function cooperates with vector < bool > edgevisited to find the unreachable path and its Node; Cut_ The pair function is based on unordered_ Map < int, int > M to count the Edge of each Node, and call search for nodes with M[Node]==1_ one_ Pair find paired nodes_ Target, this process updates M; Then use cut recursively for M[Node_target]_ Pair method; Non ring edges are removed:

 1 class Solution {
 2 private:
 3 vector<bool>edgeVisited;
 4 unordered_map<int,int>M;
 5 int search_one_pair(vector<vector<int>>& edges,int key){
 6     for(int i=0;i<edges.size();i++){
 7         if(edgeVisited[i]==true)continue;
 8         if(edges[i][0]==key){
 9             edgeVisited[i]=true;
10             return edges[i][1];
11         }
12         if(edges[i][1]==key){
13             edgeVisited[i]=true;
14             return edges[i][0];
15         }
16     }
17     return -1;
18 }
19 void Cut_pair(vector<vector<int>>& edges){
20     auto q=M.begin();
21         while(q!=M.end()){
22             if(q->second==1){
23                 q->second=0;
24                 int temp=search_one_pair(edges,q->first);
25                 M[temp]--;
26                 //cout<<q->first<<"*"<<q->second<<" ";
27                 if(M[temp])Cut_pair(edges);//Cut again or not
28             }
29             q++;
30         }
31      return;
32 }
33 public:
34     vector<int> findRedundantConnection(vector<vector<int>>& edges) {
35         edgeVisited.resize(edges.size(),false);
36         for(int i=0;i<edges.size();i++){
37             M[edges[i][0]]++;
38             M[edges[i][1]]++;
39         }
40         Cut_pair(edges);
41         for(int i=edges.size()-1;i>=0;i--){
42             if(M[edges[i][0]]>0 && M[edges[i][1]]>0){
43                 //cout<<"^"<<M[edges[i][0]]<<" "<<M[edges[i][1]]<<"^";
44                 return edges[i];
45             }
46         }
47         return {};
48     }
49 };

Time complexity: O(n^2)

Space complexity: O(n)

be careful:

unordered_ Compared with other storage structures, map helps to reduce the time complexity, otherwise it will reach the upper limit of time complexity.

 

 

Cpp solution 2 - joint search set:

analysis:

Any tree with n nodes can only have n-1 edges, and the edges on any closed loop belong to the subgraph where the two nodes are located at the same time. Using this condition, the subtrees can be merged quickly according to the egde order, and the last returned edge is the last closed loop edge in the edge;

Note: the initialization node is a single subtree, and the initial vector < int > fatherindex length is the number of nodes n = egdes size()-1.

For example 1:

 

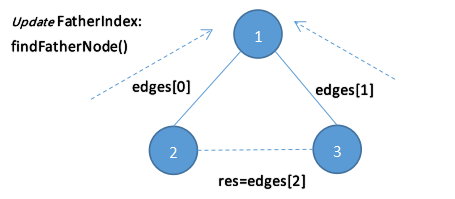
 1 class Solution {
 2 private:
 3 int findFatherNode(vector<int>& FatherIndex,int point){
 4     if(FatherIndex[point]==point)return point;
 5     FatherIndex[point]=findFatherNode(FatherIndex,FatherIndex[point]);
 6     return FatherIndex[point];
 7 }
 8 public:
 9     vector<int> findRedundantConnection(vector<vector<int>>& edges) {
10         vector<int>FatherIndex(edges.size()+1);
11         for(int i=1;i<edges.size();i++){
12             FatherIndex[i]=i;//initialize n subtrees
13         }
14         for(int i=0;i<edges.size();i++){
15             int Fres1=findFatherNode(FatherIndex,edges[i][0]);
16             int Fres2=findFatherNode(FatherIndex,edges[i][1]);
17             if(Fres1==Fres2){
18                 return edges[i];//last edge
19             }else{
20                 FatherIndex[Fres2]=Fres1;
21             }
22         }
23         return {};
24     }
25 };

Time complexity: O(n)

Space complexity: O(n)