Title Description

Given a matrix of m x n, if an element is 0, all elements of its row and column are set to 0. Please use In place Algorithms.

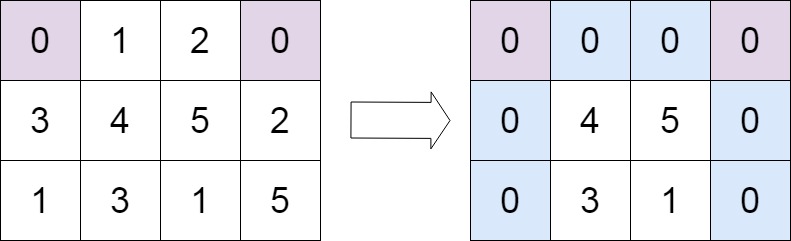
Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
Output: [[0,0,0,0], [0,4,5,0], [0,3,1,0]]

Source: LeetCode
Links:   https://leetcode-cn.com/problems/set-matrix-zeroes

Method 1: O(m + n) spatial complexity

Create two arrays row[m] and col[n] to record the row and column numbers that should be zeroed, respectively, with spatial complexity O(m + n)

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<int>row(m,0);
        vector<int>col(n,0);

        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(!matrix[i][j]){
                    row[i] = 1;
                    col[j] = 1;
                }
            }
        }

         for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(row[i]||col[j]) matrix[i][j] = 0;   
            }
        }

    }
};

Method 2: O(1) Spatial Complexity

Use the first row and the first column of the matrix to save the two arrays in method one, so there is no need to open up additional array space. However, two variables, row0 and col0, are needed to record whether the first row has zero occurrence and the second row has zero occurrence, respectively.

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int row0 = 0, col0 = 0;

        for(int i = 0; i < n; i++){
            if(!matrix[0][i]) row0 = 1;
        }
        for(int i = 0; i < m; i++){
            if(!matrix[i][0]) col0 = 1;
        }

        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                if(!matrix[i][j]){
                    matrix[0][j] = 0;
                    matrix[i][0] = 0;
                }
            }
        }

         for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                if(!matrix[0][j]||!matrix[i][0]) matrix[i][j] = 0;   
            }
        }

        if(row0){
            for(int i = 0; i < n; i++){
                matrix[0][i] = 0;
            }
        }
        if(col0){
            for(int i = 0;i < m;i++){
                matrix[i][0] = 0;
            }
        }

    }
};

Note: The treatment of zero elements in the first row and zero elements in the first column is a detail. Take the example in the figure, the fourth column in the first row is zero, and the fourth column in the output matrix should be all zero. However, in the case of a matrix, if the first row, the first column, has zero elements and is recorded in a variable, it is not possible to directly ignore the first row, the first column, and start observing and recording zero elements from the second row, the second column, because the zero element in the first row, the fourth column, as shown in the example, is ignored. Processing is also very simple, as long as the tag value of the zero element is set to 0, then the zero element as shown in the figure will naturally be treated as zero in this column.

Method 3: O(1) Spatial Complexity

This method is also the spatial complexity of O(1), but unlike method 2, method 3 only uses one extra variable.

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int col0 = 0;

        for(int i = 0; i < m; i++){
            if(!matrix[i][0]) col0 = 1;
            for(int j = 1; j < n; j++){
                if(!matrix[i][j]){
                    matrix[0][j] = 0;
                    matrix[i][0] = 0;
                }
            }
        }

        for(int i = m - 1; i >= 0; i--){
            for(int j = 1; j < n; j++){
                if(!matrix[0][j]||!matrix[i][0]) matrix[i][j] = 0;   
            }
        }

        if(col0){
            for(int i = 0;i < m;i++){
                matrix[i][0] = 0;
            }
        }

    }
};

Note that when writing code, merge loops that can be merged to optimize run time.