Leetcode94. Binary Tree Inorder Traversal

Given a binary tree, return the inorder traversal of its nodes' values.

Example:

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,3,2]

Follow up: Recursive solution is trivial, could you do it iteratively?

Three ergodic summaries

Solution a classic recursion

Middle order traversal: left subtree root node right subtree.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    getAns(root, ans);
    return ans;
}

private void getAns(TreeNode node, List<Integer> ans) {
    if (node == null) {
        return;
    }
    getAns(node.left, ans); 
    ans.add(node.val);
    getAns(node.right, ans);
}

Solution 2: stack based traversal

Thought: Thought: every node A, because the root access is in the middle, A is pushed into the stack. Then we traverse the left subtree, then visit A, and finally traverse the right subtree. After visiting A, A can go out of the stack. Because both A and its left subtree have been accessed.

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    while (cur != null || !stack.isEmpty()) {
        //The node is not empty and keeps pressing
        while (cur != null) {
            stack.push(cur);
            cur = cur.left; //Consider left subtree
        }
        //If the node is empty, the stack will be released
        cur = stack.pop();
        //Current value added
        ans.add(cur.val);
        //Consider right subtree
        cur = cur.right;
    }
    return ans;
}

		  ...
        1 (1) stack is [..., 1,2,4], at this time, cur is empty, stop stack pressing and start to stack, cur = node4, cur = node4.right = null
      /(2) Stack [..., 1,2], cur is empty, continue to stack, cur = node2, cur = node2.right = node5 
     2 (3) stack is [... 1], cur = node5 is not empty, so node5 presses the stack first and then exits the stack, cur = node5.right = null
    /\ (4) if the stack is [... 1] and cur is empty, the stack will be out of node1, and then analyze the right subtree of node1.
   4   5 

        1
      /   \
     2     3
    / \   /
   4   5 6

 push   push   push   pop     pop    push     pop     pop 
|   |  |   |  |_4_|  |   |   |   |  |   |    |   |   |   |  
|   |  |_2_|  |_2_|  |_2_|   |   |  |_5_|    |   |   |   |
|_1_|  |_1_|  |_1_|  |_1_|   |_1_|  |_1_|    |_1_|   |   |
ans                  add 4   add 2           add 5   add 1
[]                   [4]     [4 2]           [4 2 5] [4 2 5 1]
 push   push   pop          pop 
|   |  |   |  |   |        |   |  
|   |  |_6_|  |   |        |   |  
|_3_|  |_3_|  |_3_|        |   |
              add 6        add 3
              [4 2 5 1 6]  [4 2 5 1 6 3]

Solution 3: Morris Traversal

Solution one and solution two are essentially the same, both need O(h) space to save the information of the previous layer. Since the middle order traversal is the left subtree - root node - right subtree, we can save the current root node, and then traverse the left subtree. After the left subtree traversal, we can return to the current root node, so we do not need to store the information of the previous layer.

① The current root node has a left subtree: the last node traversed by the left subtree must be a leaf node, and its left and right children are null. We store the right child pointing to the current root node, so we don't need extra space. In this way, after traversing the current left subtree, you can return to the root node.
② The left subtree of the current root node is empty, so we only need to save the value of the root node, and then consider the right subtree.

thinking
Note that the current traversal node is cur.

1. cur.left is null, save the value of cur, update cur = cur.right

2. Cur.left is not null. Find the rightmost node of cur.left subtree and record it as last

   1. If last.right is null, update cur = cur.left with last.right = cur

   2. last.right is not null, indicating that it has been accessed before. The second time it comes here, it indicates that the current subtree traversal is complete, saves the cur value, and updates cur = cur.right

public List<Integer> inorderTraversal3(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    TreeNode cur = root;
    while (cur != null) {
        //Situation 1
        if (cur.left == null) {
            ans.add(cur.val);
            cur = cur.right;
        } else {
            //Find the rightmost node of the left subtree
            TreeNode pre = cur.left;
            while (pre.right != null && pre.right != cur) {
                pre = pre.right;
            }
            //Situation 2.1
            if (pre.right == null) {
                pre.right = cur;
                cur = cur.left;
            }
            //Situation 2.2
            if (pre.right == cur) {
                pre.right = null; //It can be restored to null here
                ans.add(cur.val);
                cur = cur.right;
            }
        }
    }
    return ans;
}

• Time complexity: O(n)O(n)O(n)
• Space complexity: O(1)O(1)O(1)

Graphical Morris method

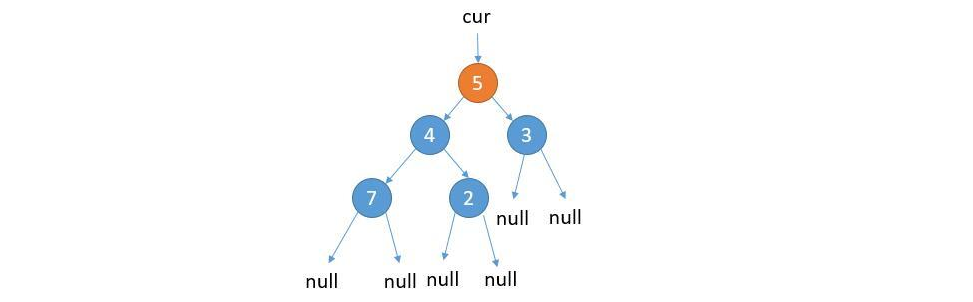
① Cur - > left is not null. Point the right child of the rightmost node in the left subtree of cur to cur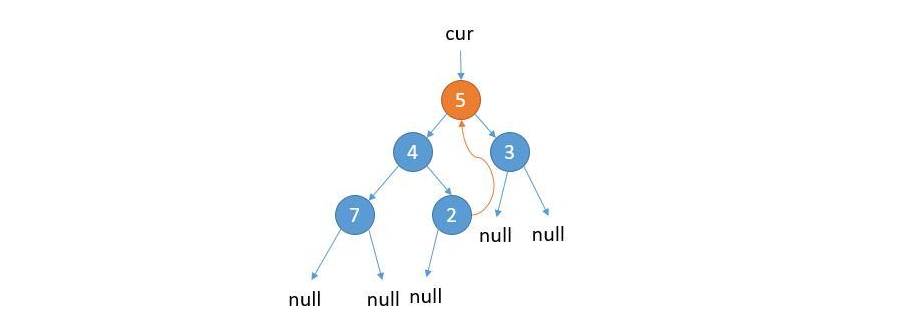

② Update cur = cur.left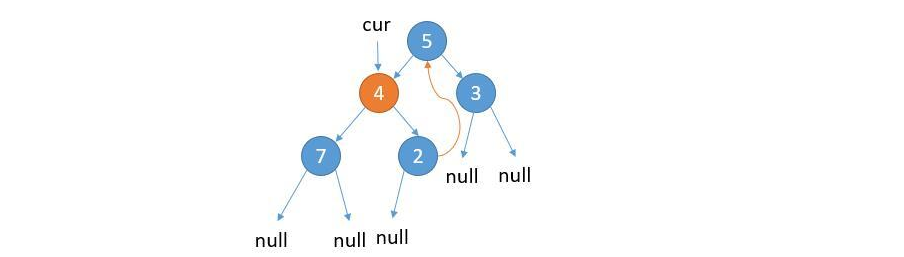

③ As shown in the above figure, the current cur.left is not null. Point the right child of the rightmost node of the left subtree of cur to cur

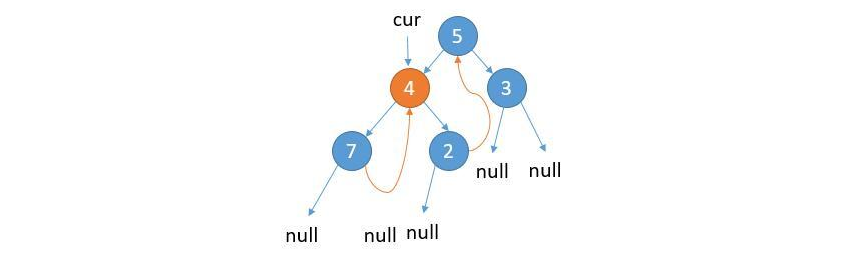
④ Update cur = cur.left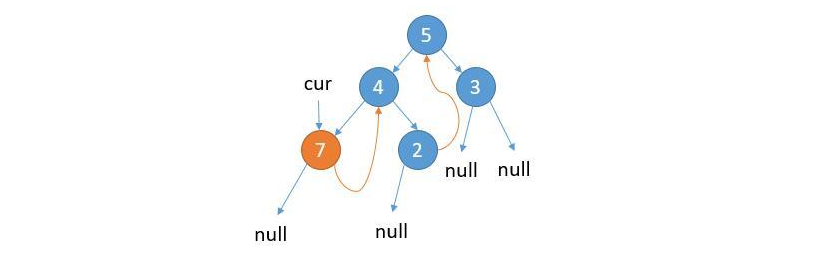

⑤ cur.left is null, save the value of cur, and update cur = cur.right.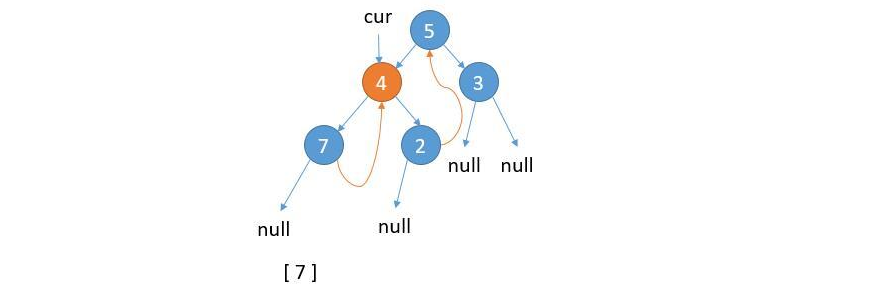

⑥ cur.left is not null. The right child of the rightmost node in the left subtree of cur has pointed to cur. Save the value of cur and update cur = cur.right.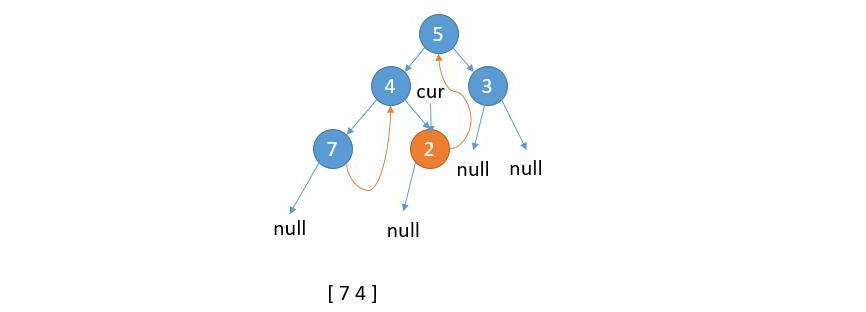

⑦ cur.left is null, save the value of cur, update cur = cur.right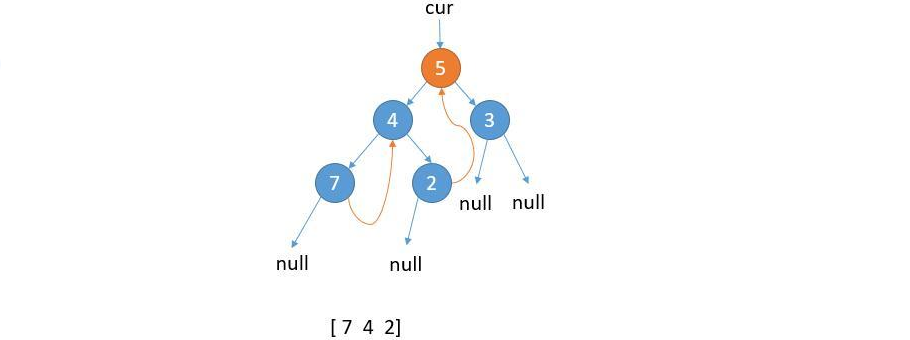

⑧ cur.left is not null. The right child of the rightmost node in the left subtree of cur has pointed to cur. Save the value of cur and update cur = cur.right.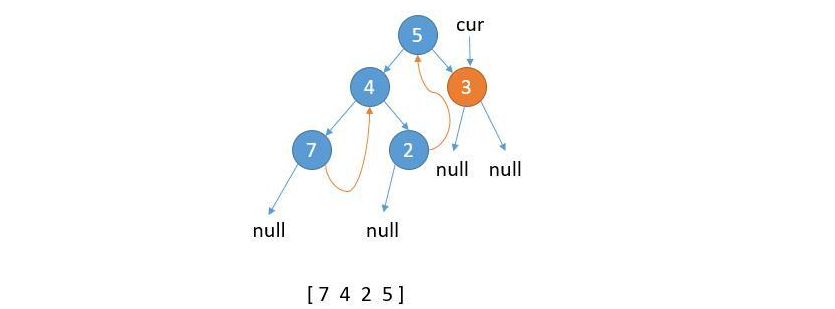

⑨ cur.left is null, save the value of cur, and update cur = cur.right.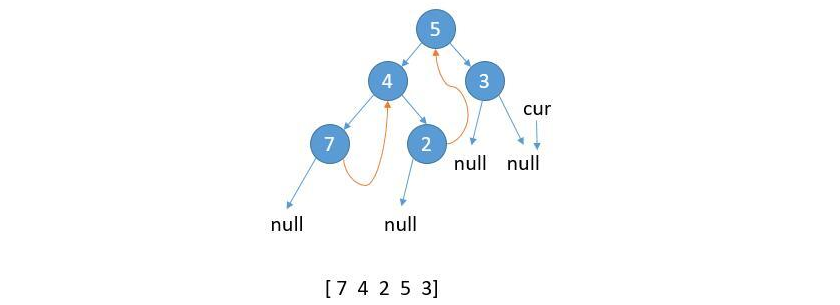

⑩ cur points to null, ending traversal.

C++ solution

Iterative solution using stack

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> nodes;
        stack<TreeNode*> todo;
        while (root || !todo.empty()) {
            while (root) {
                todo.push(root);
                root = root -> left;
            }
            root = todo.top();
            todo.pop();
            nodes.push_back(root -> val);
            root = root -> right;
        }
        return nodes;
    }
};

Recursive solution

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> nodes;
        inorder(root, nodes);
        return nodes;
    }
private:
    void inorder(TreeNode* root, vector<int>& nodes) {
        if (!root) {
            return;
        }
        inorder(root -> left, nodes);
        nodes.push_back(root -> val);
        inorder(root -> right, nodes);
    }
};

Morris traversal

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> nodes;
        while (root) {
            if (root -> left) {
                TreeNode* pre = root -> left;
                while (pre -> right && pre -> right != root) {
                    pre = pre -> right;
                }
                if (!pre -> right) {
                    pre -> right = root;
                    root = root -> left;
                } else {
                    pre -> right = NULL;
                    nodes.push_back(root -> val);
                    root = root -> right;
                }
            } else {
                nodes.push_back(root -> val);
                root = root -> right;
            }
        }
        return nodes;
    }
};