catalogue
2.1 establishment of large root pile
2.7 finding and minimum K-pair numbers
1, Related concepts of heap
1.1 reactor
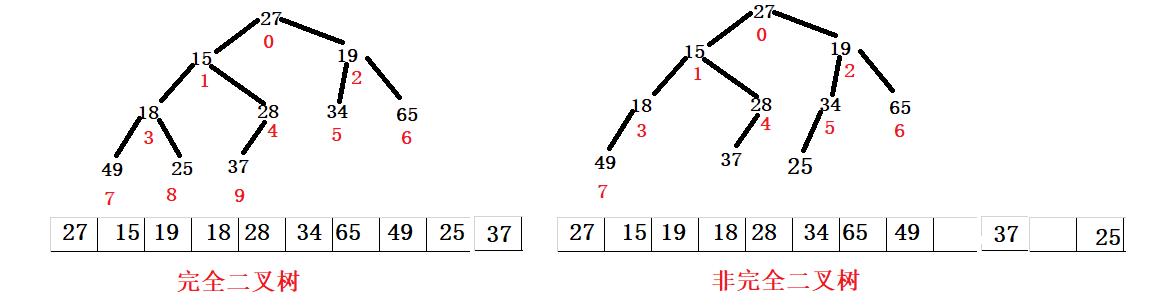
Heap: logically, it is a complete binary tree, which is physically stored in an array.
Heap is a complete binary tree logically, and the values are stored in an array in a sequential manner.
Sequential storage: store the binary tree in the array by "sequence traversal". Sequential storage is generally suitable for representing complete binary trees, and incomplete binary trees will waste space.
1.2 subscript relationship
This subscript relation is for a complete binary tree
Known: parent node subscript = parent, left child subscript = 2 * parent + 1, right child subscript = 2 * parent + 2
Known: child node = child, parent node subscript = (child - 1) / 2
1.3 classification
Small root heap: the parent node < left and right child nodes, and the size of the left and right children does not matter.
Large root heap: parent node > left and right child nodes. The size of left and right children does not matter.
Only when each sub tree of the whole binary tree is a large root pile / small root pile, the whole tree is a large root pile / small root pile.
2, Manually implement heap
2.1 establishment of large root pile
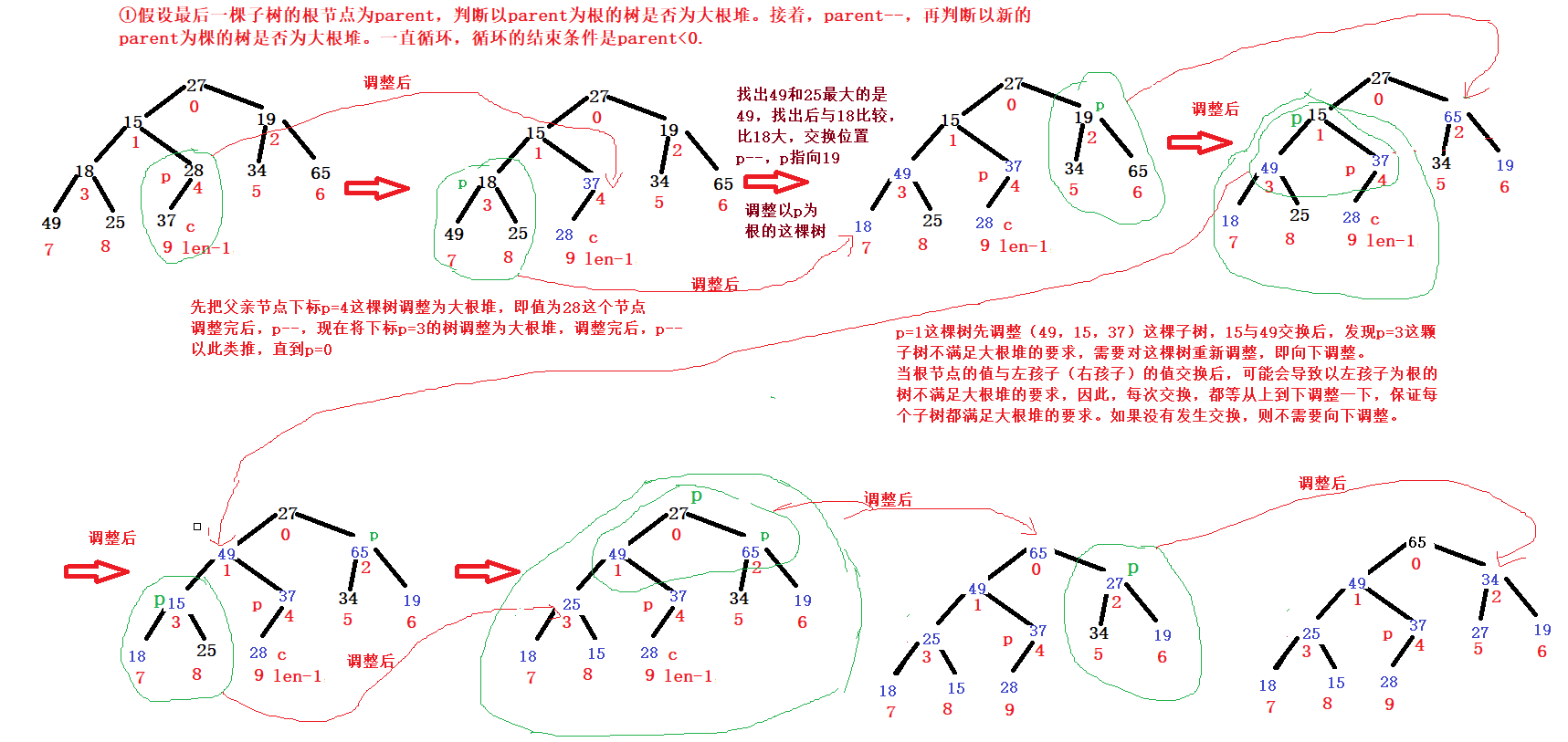
There are two main steps to build a large root heap.
Step 1: locate the last subtree.
Assuming that the length of the array is len and the subscript of the last element is len-1, that is, the subscript of the child node of the last tree is len-1, then the subscript of the parent node of the last tree is (len-1-1)/2.

Step 2: start from the last subtree, judge whether it is a large root heap, and adjust it to a large root heap. The strategy adopted is "downward adjustment".
① Assuming that the root node subscript of the last subtree is parent, judge whether the tree with parent as the root node subscript is a large root heap. If it is not a large root heap, it needs to be adjusted to a large root heap. Next, subtract 1 from the parent, and then judge whether the subscript of the new parent is the root node is a large root heap. Subtract 1 from the parent, and the cycle will continue. The end condition of the cycle is parent < 0.
② Every time you adjust the large root heap, the subtree may no longer meet the requirements of the large root heap. Therefore, you need to adjust downward from the parent to ensure that each subtree is a large root heap. The end condition of adjustment is child > = len.

public class TestDemo {
public int[] elem;
public int usesize; // Represents the number of elements in the array
public int capacity = 10; // Initial capacity of the array
public TestDemo(){
this.elem = new int[10];
}
public void createBigHeap(int[] array){
if(array == null){
return;
}
if(array.length >= this.capacity){ // If the length of elem is greater than capacity, it needs to be expanded
this.elem = Arrays.copyOf(this.elem,this.capacity*2);
}
for(int i=0;i<array.length;i++){
this.elem[i] = array[i];
usesize++;
}
for(int parent = (this.usesize-1-1)/2 ; parent>=0 ; parent--) {
shiftDown(parent,this.usesize);
}
}
// Adjust non recursive down
public void shiftDown(int parent,int usesize){
int child = 2*parent+1;
while(child < this.usesize){
if(child+1<this.usesize && this.elem[child] < this.elem[child+1]){
child++; // Let the child subscript store the subscript of the child node with the largest value
}
if(this.elem[child]>this.elem[parent]){
int tmp = this.elem[child];
this.elem[child] = this.elem[parent];
this.elem[parent] = tmp;
// After the exchange, you need to adjust / ensure that each subtree below meets the condition of large root heap
parent = child;
child = 2*parent+1;
}else{
break;
}
}
}
// Adjust recursion down
public void shiftDown2(int parent){
int child = 2*parent+1;
if(child >= this.usesize){
return;
}
if(child+1 < this.usesize && this.elem[child]<this.elem[child+1]){
child++; // Let the child store the subscript with the largest value of the left and right children
}
if(this.elem[child] > this.elem[parent]){
int tmp = this.elem[child];
this.elem[child] = this.elem[parent];
this.elem[parent] = tmp;
parent = child;
shiftDown2(parent);
}
}
}2.2 adding data
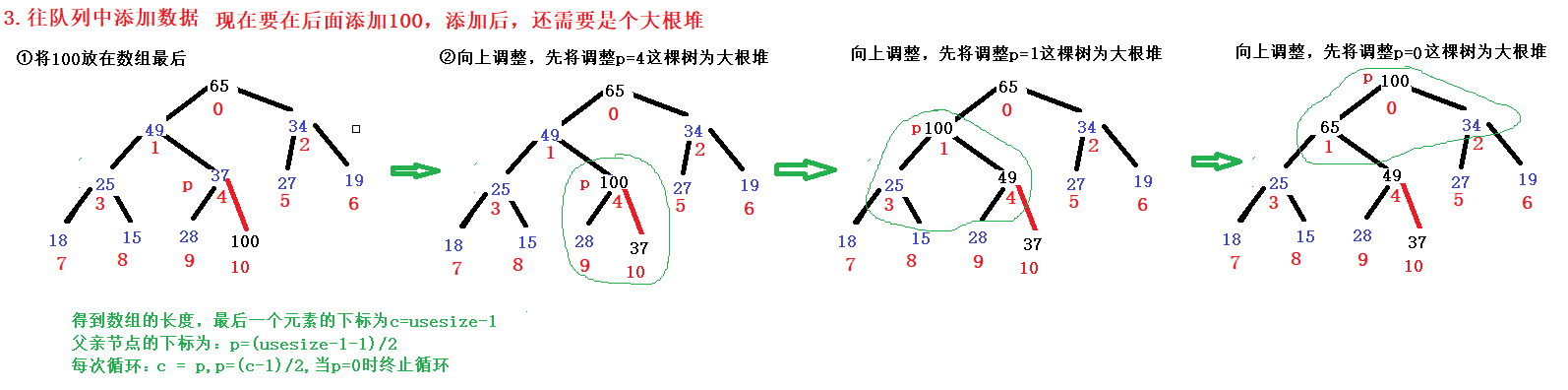
After adding data to the large root heap, you need to ensure that the heap is still a large root heap after adding. Adopt the strategy of "upward adjustment".
Method: put the added data at the end of the queue and adjust it upward
public void push(int val){
// Putting val in the end, changing the last element and heap element.
if(this.elem.length > this.usesize){ // If the length of elem is greater than capacity, it needs to be expanded
this.elem = Arrays.copyOf(this.elem,this.capacity*2);
}
this.elem[usesize] = val;
usesize++;
int parent = (this.usesize-1-1)/2;
int child = this.usesize-1;
while(parent >= 0){
if(this.elem[parent] < this.elem[child]){
int tmp = this.elem[parent];
this.elem[parent] = this.elem[child];
this.elem[child] = tmp;
child = parent;
parent = (child-1)/2;
}else{
break;
}
}
}2.3 pop up the top data
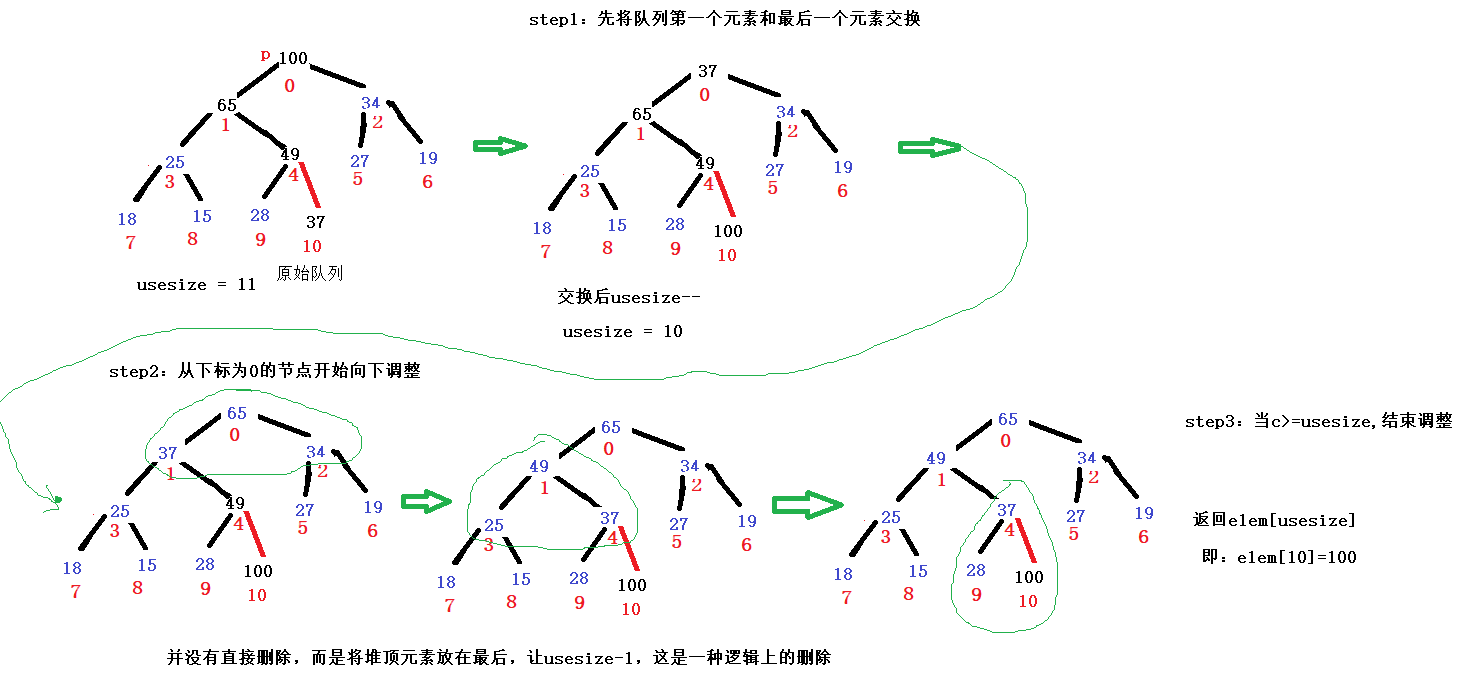
Pop up the heap top data does not really delete the elements from the heap, but puts the heap top elements at the end of the heap, usesize-1 of the heap. Logically, the heap does not contain this element, and the length of the heap is subtracted by 1
Steps:
Step 1: swap the top element and the last element.
Step 2: start from the top of the stack and adjust downward. Make sure that each tree is a large top pile.
public int pop(){
// Swap the first element and the last element first
int tmp = this.elem[0];
this.elem[0] = this.elem[this.usesize-1];
this.elem[this.usesize-1] = tmp;
this.usesize--;
// Adjust the tree with parent = 0 downward
shiftDown2(0);
return this.elem[this.usesize];
}2.4 viewing top data
public int peek(){
if(this.usesize == 0){
throw new RuntimeException("null!");
}
return this.elem[0];
}2.5 topK problem
Problem Description: find the first K largest / smallest elements from an array.
Problem deformation: find the K-th largest / smallest element from an array.
Take finding the first K smallest elements in the array as an example.
Traditional thinking: call the sort function to sort the array in descending order and select the first K.
When you encounter this problem, you should think of the priority queue, that is, the heap.
Idea 1: establish a small root pile and take the first K.
Evaluation: the method is wrong. The small root heap can only ensure that the top elements of the heap are the smallest, not the first K elements.
Idea 2: create a small root heap and pop up the top elements one by one
Evaluation: the method is correct. Every time the heap top element is ejected, the new heap will be adjusted to a small root heap to ensure that the heap top element is the smallest.
However, the time complexity is high, which is N*logN.
Idea 3: build the first k elements into a large root heap. Starting from the K+1 element, compare it with the top element. If it is smaller than the top element, the top element will go out of the heap and this element will go into the heap.
Evaluation: this method does not sort the whole, and also controls the size of heap building. The time complexity is N*logK.

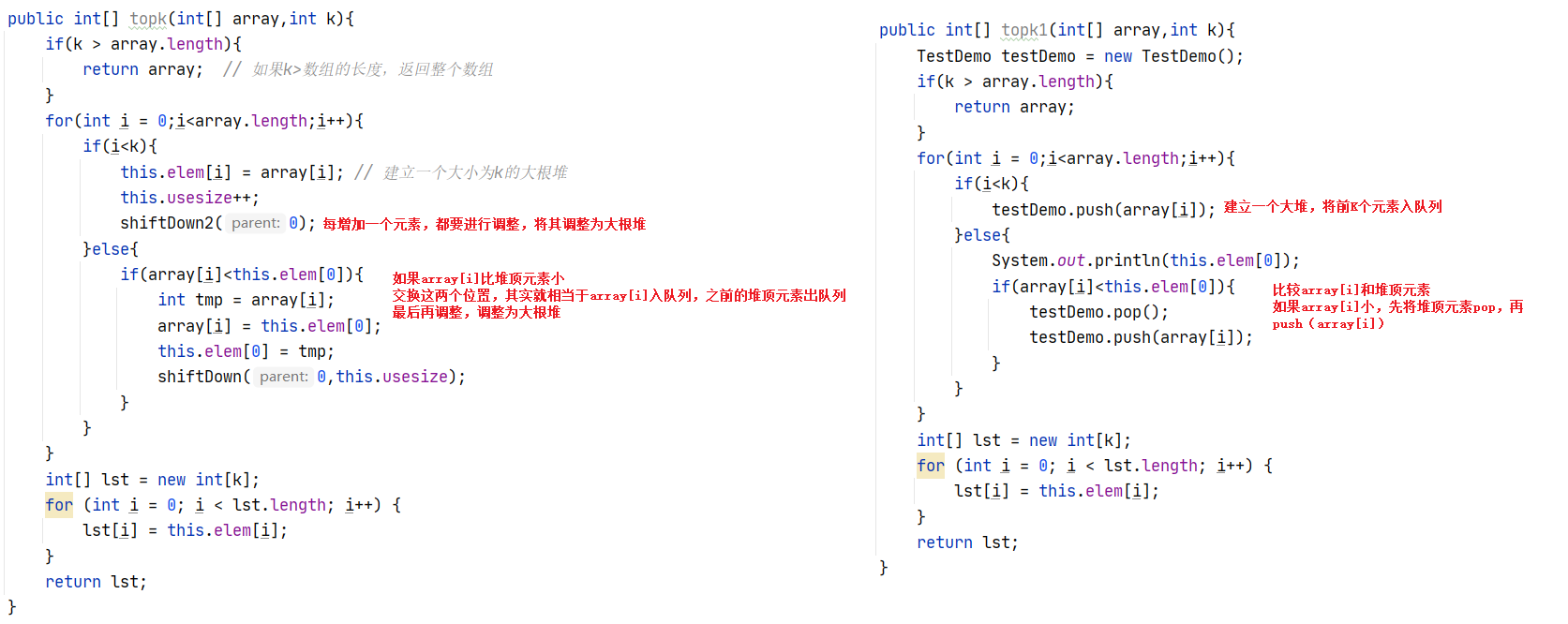
// Call the written code such as heap building, pop and push
public int[] topk1(int[] array,int k){
TestDemo testDemo = new TestDemo();
if(k > array.length){
return array;
}
for(int i = 0;i<array.length;i++){
if(i<k){
testDemo.push(array[i]);
}else{
System.out.println(this.elem[0]);
if(array[i]<this.elem[0]){
testDemo.pop();
testDemo.push(array[i]);
}
}
}
int[] lst = new int[k];
for (int i = 0; i < lst.length; i++) {
lst[i] = this.elem[i];
}
return lst;
}
// The second method
public int[] topk(int[] array,int k){
if(k > array.length){
return array; // If k > the length of the array, the entire array is returned
}
for(int i = 0;i<array.length;i++){
if(i<k){
this.elem[i] = array[i]; // Create a large root heap of size k
this.usesize++;
shiftDown(0);
}else{
if(array[i]<this.elem[0]){
int tmp = array[i];
array[i] = this.elem[0];
this.elem[0] = tmp;
shiftDown(0,this.usesize);
}
}
}
int[] lst = new int[k];
for (int i = 0; i < lst.length; i++) {
lst[i] = this.elem[i];
}
return lst;
}Summary of best practices:

2.6 heap sorting
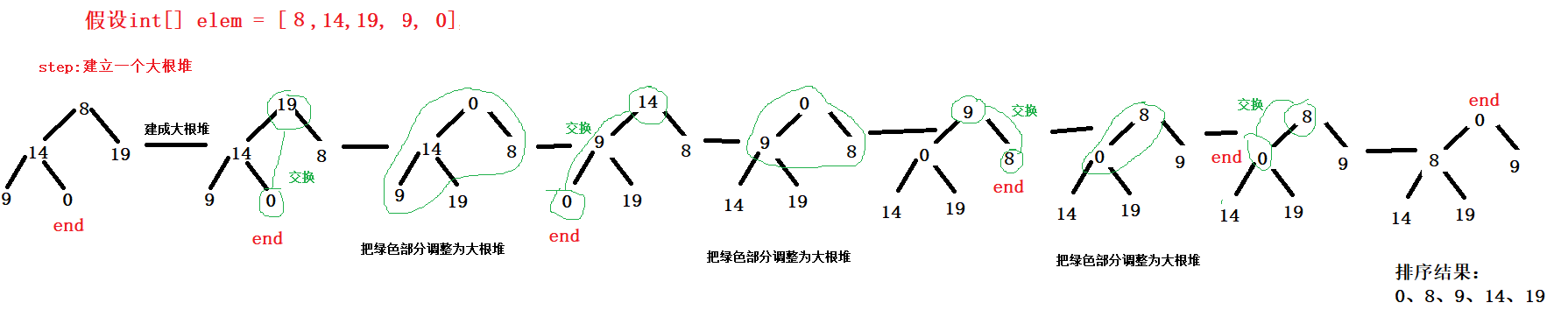
Suppose you sort an array from small to large.
Idea:
Use end as the boundary between the sorted and unordered parts of the array.
At the beginning, it is a large root heap. The whole array does not meet the requirements from small to large, so end = the length of the array - 1
After exchanging the heap top element and the end subscript element, put the largest element at the end position and the largest element at the end, which proves that the element has been ordered. Therefore, end-1 points to the next unordered element.
Create a large root heap – "exchange the top elements with the end subscript elements –" end subscript minus 1 – "adjust down – > then exchange the top elements with the end subscript elements –" end subscript minus 1 – "adjust down" ---- and cycle until end < 0
public int[] sorted(int[] array){
if(array == null){
return null;
}
int end = this.usesize;
createBigHeap(array);
while(end >= 1){
int tmp = this.elem[0];
this.elem[0] = this.elem[usesize-1];
this.elem[usesize-1] = tmp;
end--;
shiftDown(0,end);
}
int[] lst = new int[this.elem.length];
for(int i = 0;i<this.elem.length;i++){
lst[i] = this.elem[i];
}
return lst;
}2.7 finding and minimum K-pair numbers
1. Problem description and summary
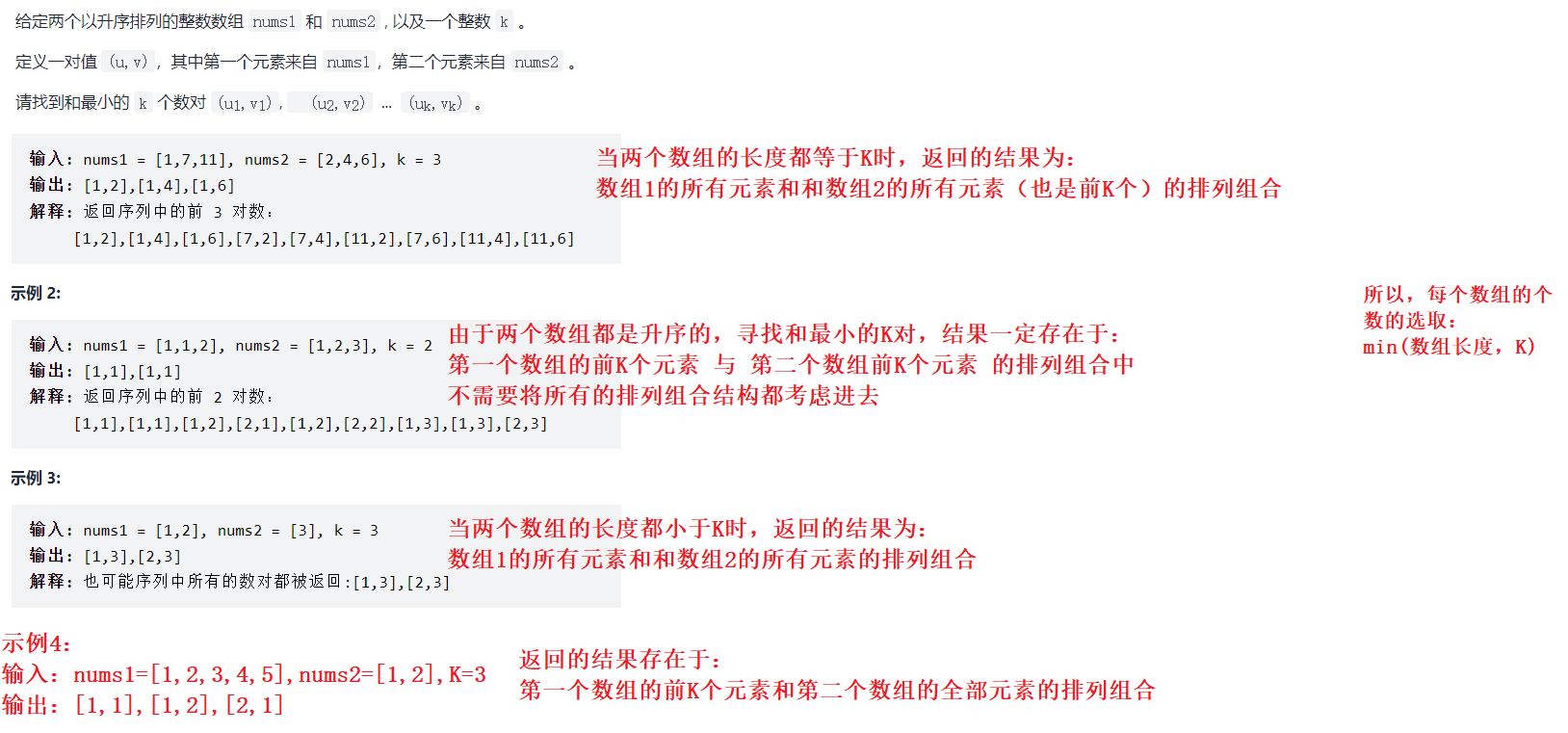

public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
List<List<Integer>> listList = new ArrayList<>();
PriorityQueue<List<Integer>> priorityQueue = new PriorityQueue<>(new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
return (o2.get(0)+o2.get(1))-(o1.get(0)+o1.get(1));
}
});
for(int i = 0; i<Math.min(k,nums1.length) ;i++){
for(int j =0; j<Math.min(k,nums2.length); j++){
List<Integer> list =new ArrayList<>();
list.add(0,nums1[i]);
list.add(1,nums2[j]);
listList.add(list);
if(listList.size() <= k){
priorityQueue.add(list);
}else{
List<Integer> ret = priorityQueue.peek();
int peeksum = ret.get(0)+ret.get(1);
if(nums1[i]+nums2[j] < peeksum){
List<Integer> list1 = new ArrayList<>();
list1.add(0,nums1[i]);
list1.add(1,nums2[j]);
priorityQueue.poll();
priorityQueue.offer(list1);
}
}
}
}
List<List<Integer>> list2 =new ArrayList<>();
while(! priorityQueue.isEmpty()){
List<Integer> lst = priorityQueue.poll();
list2.add(lst);
}
return list2;
}3, Priority queue in Java
The priority queue in Java is PriorityQueue
Common functions:
| Throw exception | Return special value | |
| Queue | add | offer |
| Out of queue | remove | poll |
| Team leader element | element | peek |
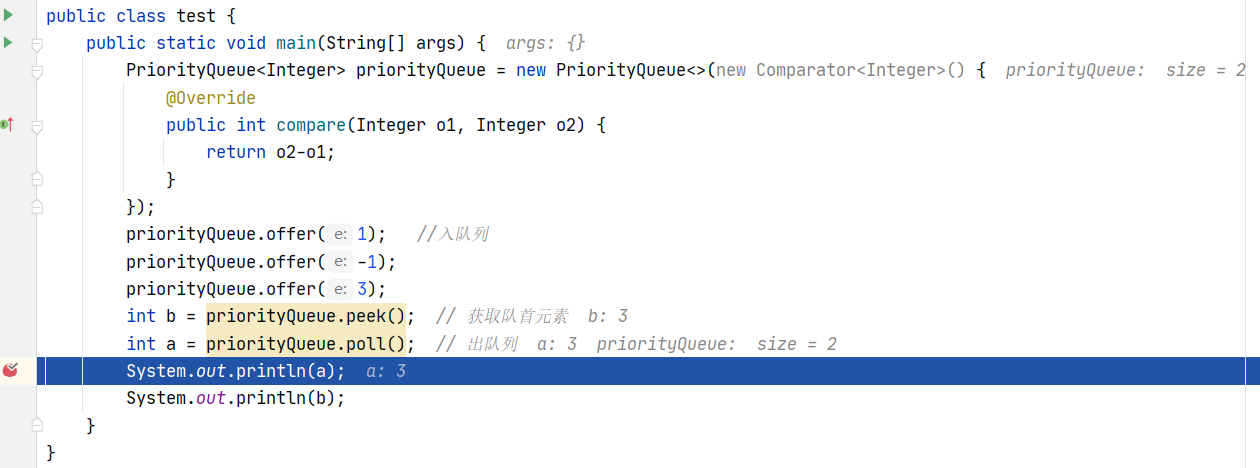
public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(1); //Queue
priorityQueue.offer(-1);
priorityQueue.offer(3);
int b = priorityQueue.peek(); // Get team leader element
int a = priorityQueue.poll(); // Out of queue
System.out.println(a);
System.out.println(b);
}Next, learn more about PriorityQueue through a few small questions
Question 1: is the bottom layer of PriorityQueue a large root heap or a small root heap?
Answer: small root pile

Question 2: the bottom layer of PriorityQueue is a small root heap by default. How to use PriorityQueue to create a large root heap?
Answer: pass in a comparator
PriorityQueue has more than one constructor

public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
priorityQueue.offer(1); //Queue
priorityQueue.offer(-1);
priorityQueue.offer(3);
int b = priorityQueue.peek(); // Get team leader element
int a = priorityQueue.poll(); // Out of queue
System.out.println(a);
System.out.println(b);
} Question 3: PriorityQueue < integer > PriorityQueue = new PriorityQueue < > (); What is the default size of an object after new?
Question 3: PriorityQueue < integer > PriorityQueue = new PriorityQueue < > (); What is the default size of an object after new?
Answer: 11

Question 4: how to expand the capacity when the number of elements in the queue exceeds the length of the queue?
Answer: the grow th function is called
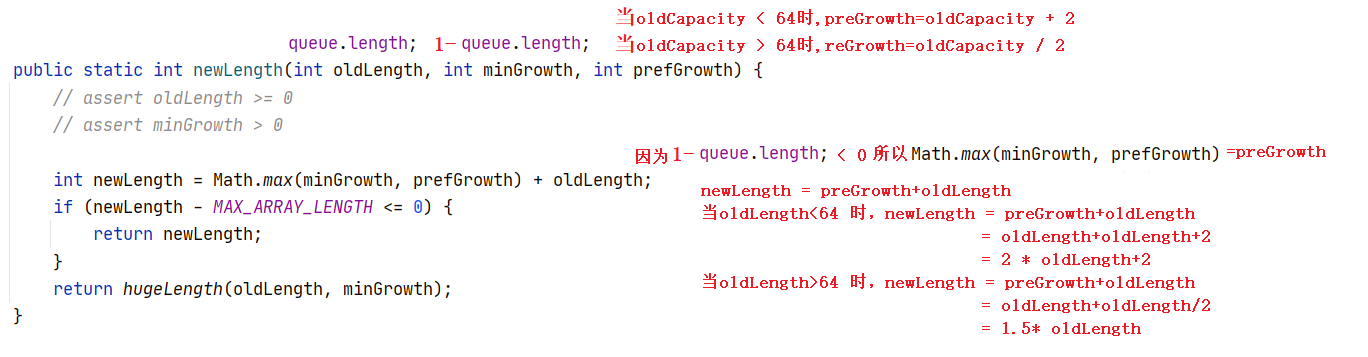
When the array length < 64, the new array length = 2 * the original array length + 2
When the array length > 64, the new array length = 1 5 * original array length
Source code:
① Use the offer function to add elements to the queue. When the array length exceeds the default length, the function called is grow()
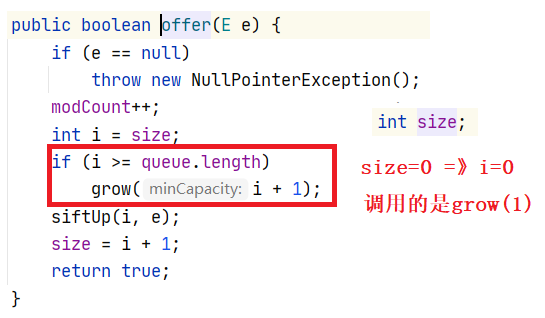
② Next, look at the growth () function. The parameter passed in is 1

③ to find the newCapacity in the growth() function, you need to call arrayssupport Newlength function
4, Summary
Firstly, we share how to realize the algorithms of creating large root heap, adding elements, deleting top elements, heap sorting, topK problem, and minimum K-pair number The core of creating large root heap, deleting heap top elements and heap sorting is downward adjustment, and the core of adding elements is upward adjustment The core of the topK problem and the smallest K-pair number is to put the first K elements into the heap and compare the other elements with the top of the heap
Then, the PriorityQueue in java is shared. By default, the PriorityQueue establishes a small heap, and the capacity expansion method is that when the array length is < 64, the new array length = 2 * the original array length + 2, and when the array length is > 64, the new array length = 1 5 * original array length If you need to create a large number of new PriorityQueue objects, you can pass in a comparator