brief introduction

Level DB accesses data with the structure of MemTable, whose core is level::MemTable::Table, that is, typedef SkipList < const char*, Key Comparator > level::MemTable::Table. SkipList knows by name. Skip list It is a data structure that allows quick queries of a linked list of ordered and continuous elements. This is a "space for time" approach, it is worth noting that these lists are orderly.

For this jump table, I looked up the analysis given by William Pugh.

Skip lists are a data structure that can be used in place of balanced trees. Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

That is to say, the core is stochastic algorithm. A spectral stochastic algorithm is very important for jump tables.

Now let's analyze the charm of springsheet with code and illustration.

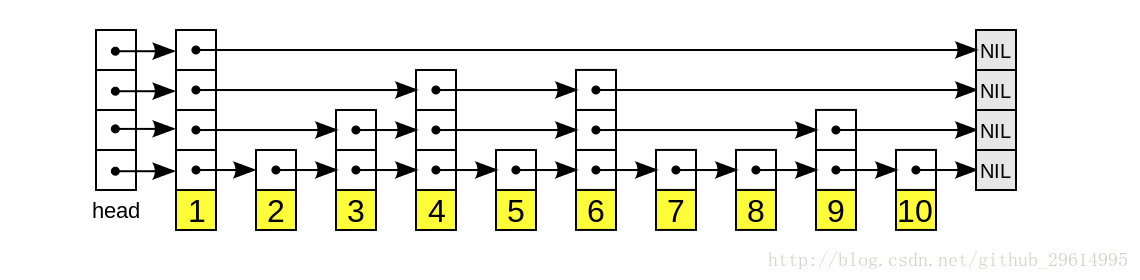
Jump table data storage model

The data structure of the jump table is as follows:

template <typename Key, typename Value>
class SkipList {
private:
    struct Node; // Declare node structure
    
public:
  explicit SkipList(); 

private:
  int level_;  // Jump table level
  Node* head_; // Header Node List of Jump Table
  unit32_t rnd_; // Random Number Factor
  
  // Generating Node Method
  Node* NewNode(int level, const Key& key,  const Value& value);
 
  Node* FindGreaterOrEqual(const Key& key, Node** prev) const;
  
};

Node data structure:

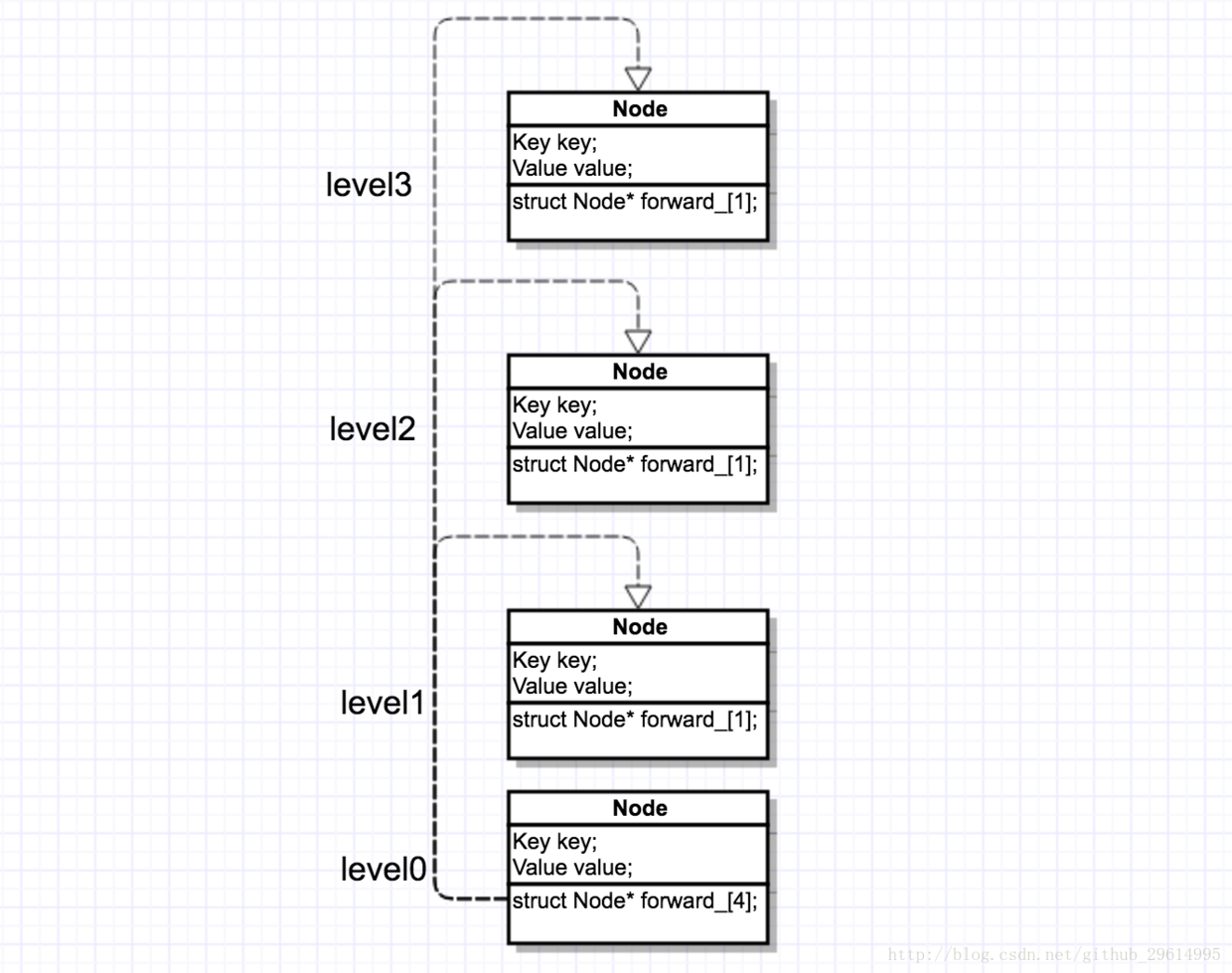
template <typename Key, typename Value>
struct SkipList<Key, Value>::Node {

  explicit Node(const Key& k, const Value& v) : key(k), value(v) {}

  Key key;  
  Value value;
  
  void SetNext(int i, Node* x);  
  Node* Next(int i)；
  
private:
  struct Node* forward_[1]; // The list of node arrays, which is more important, will be described in detail later. If you do not understand this variable, it will be difficult to understand the jump table.
}

Look at the overall structure through the diagram

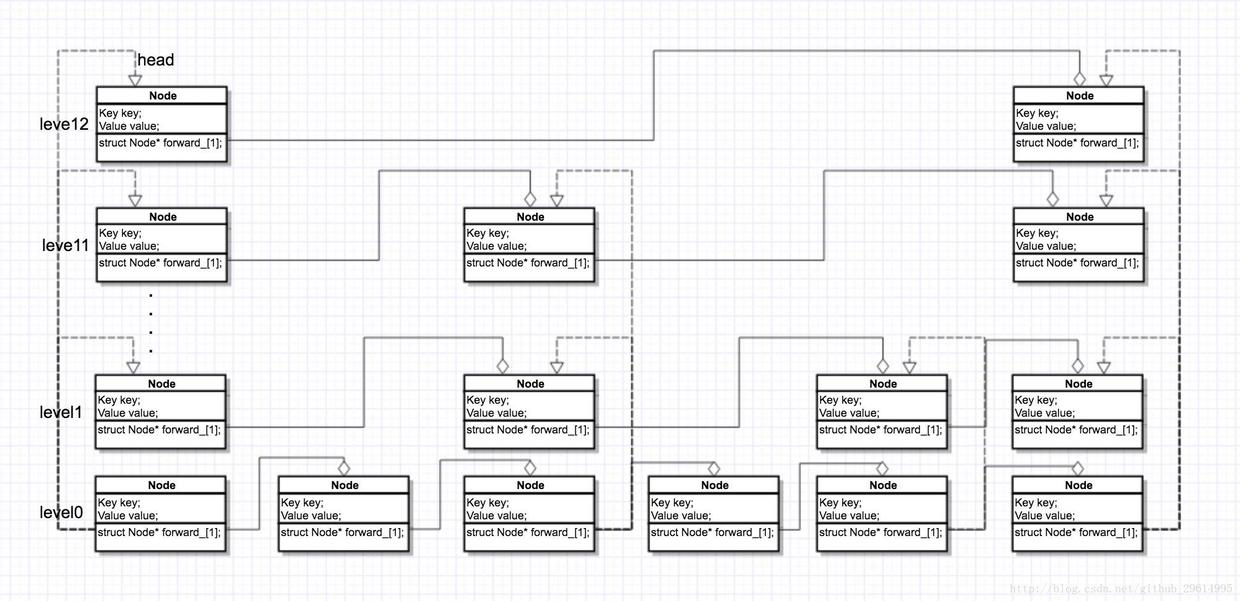
ps: dotted line links in graphs express array relations and realize the link list relationship of identification pointer

Let's assume that level is a 4-level jump chart. The forward_variable is an array of pointers, pointing to the list of the next node (black filling arrows), and at the same time, an array of these lists (transparent filling arrows) is a data structure that forms the list we need.

Later we will call the vertical (dowm) nodes in the graph an array of nodes and the horizontal (left) nodes a list of nodes.

Initialization jump table

First, to implement this structure, let's initialize the jump table.

enum {kMaxLevel = 12}; // Here, the default jump table is initialized to have a maximum height of 12 layers.

template <typename Key, typename Value>
SkipList<Key, Value>::SkipList() : head_(NewNode( kMaxLevel, 0, 0)), rnd_(0xdeadbeef)
{
  // Initialize all head node arrays
  for (int i = 0; i < kMaxLevel; ++i) {
    head_->SetNext(i, nullptr); // Setting Layer i Nodes
  }
}

Now our structure is as follows

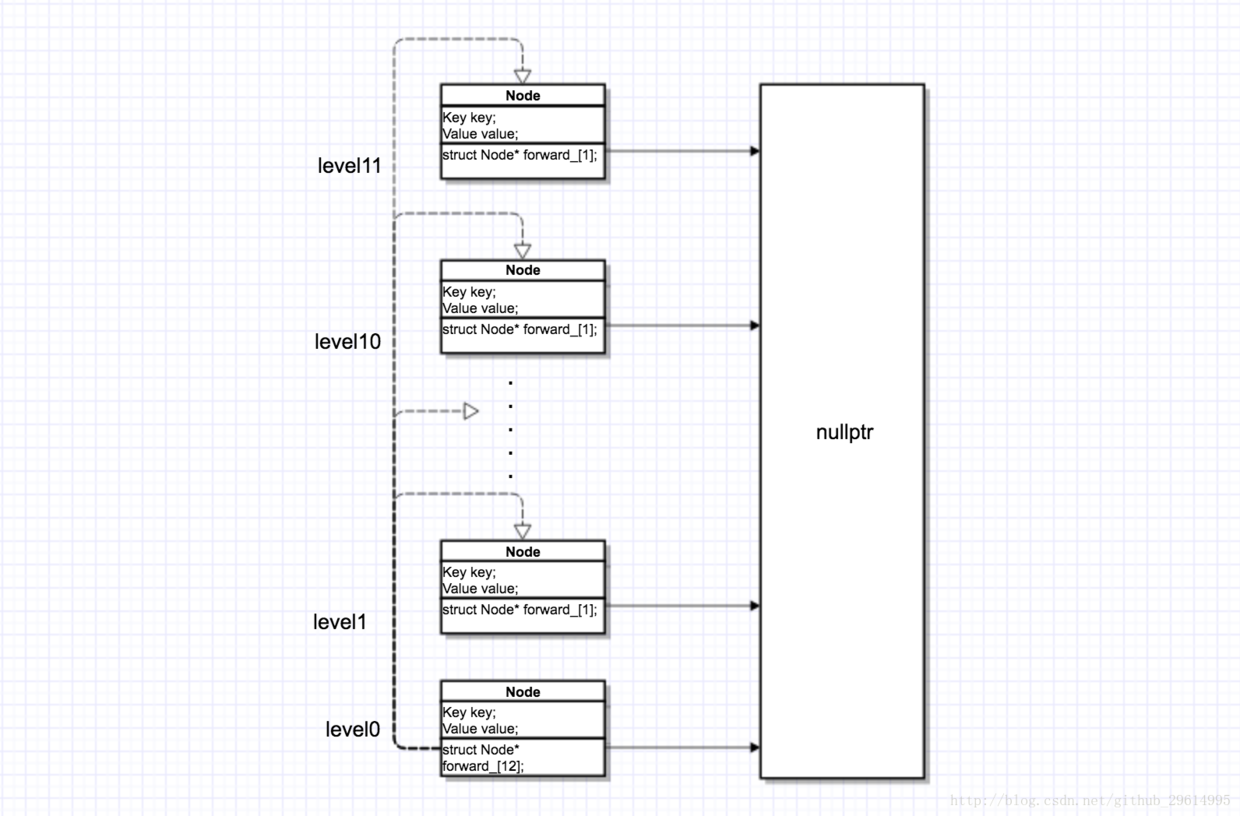
Of course, these nodes are empty. NewNode method view

Insert operation

The insertion operation is divided into two steps:

1. Find the list at each level and know where to insert it (because you want to keep the order)
2. Update node pointer and jump table height

Step one:

template <typename Key, typename Value>
typename SkipList<Key, Value>::Node*
SkipList<Key, Value>::FindGreaterOrEqual(const Key& key, Node** prev) const
{
  Node* x = head_, *next = nullptr;

  int level = level_ - 1;
  
  // Find the location to insert from the top down
  // Fill in prev, which is used to record the position of jump points at each level
  for (int i = level; i >= 0 ; --i) {
    while ( (next = x->Next(i)) && next->key < key) {
      x = next;
    }
    if (NULL != prev) {prev[i] = x;}
  }
  return next;  // Return to the location of the node most suitable for insertion at level 0
};

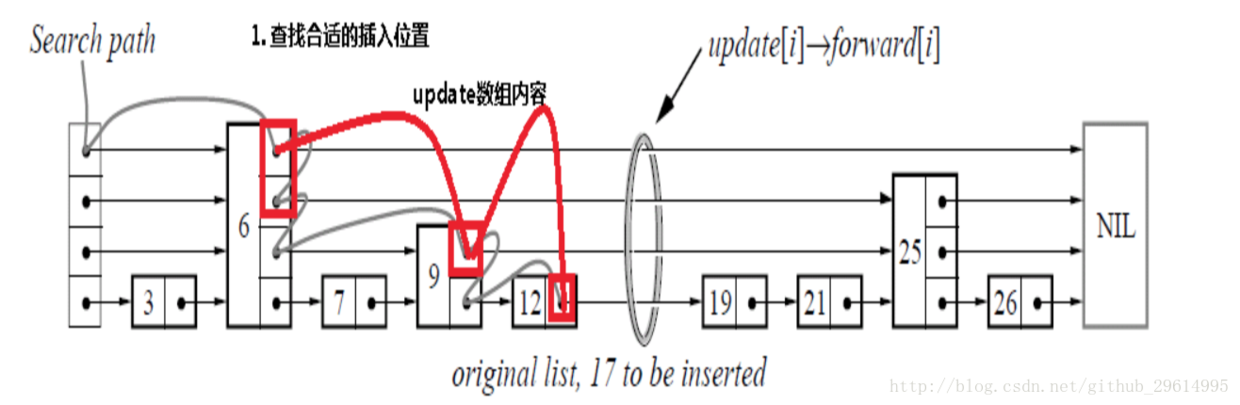
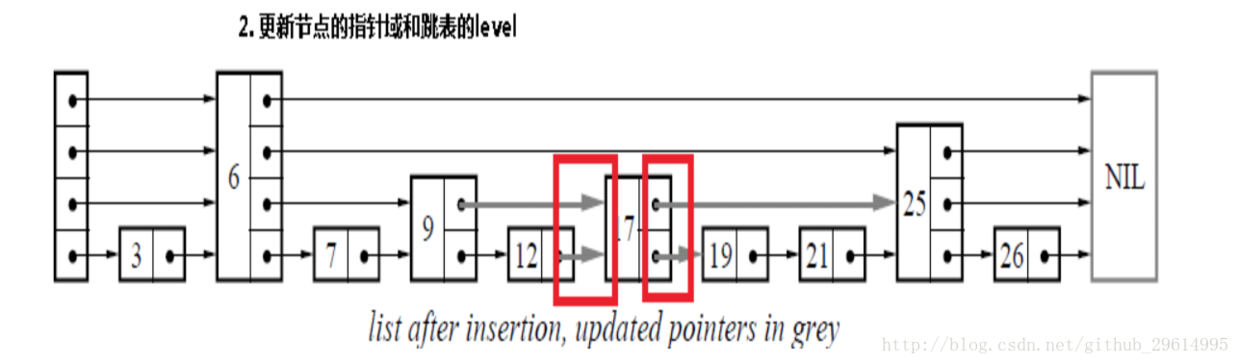
The first step is to insert key=17 into the jump table as shown in Figure 3.1. It can be seen that the jump table keeps looking for jump points, recording jump points (red box points, we hereinafter referred to as jump points), looking for the location of the insertion. For example, after running the above code in Figure 3.1, the next node with key=12 is returned, because key=17 is greater than 12, less than 19.

Figure 3.1

The second step:

template <typename Key, typename Value>
bool SkipList<Key, Value>::Insert(const Key& key, const Value& value) {
  
  /** Step 1*/  
  // prev is used to record the location of hops at each level
  Node* prev[kMaxLevel];

  // Find the list at each level and know where to insert it (because you want to keep the order)
  Node* next = FindGreaterOrEqual(key, prev);
    
  int level;    
  
  // Can't insert the same key
  if ( next && next->key == key ) {
    return false;
  }
  
  /** The second part of the implementation, the second step of the implementation of the code as shown in Figure 3.2*/
  // Generate a random layer k
  level = randomLevel();
  if (level > level_) {
    for (int i = level_; i < level; ++i) {
      prev[i] = head_; // New Layer Initialization
    }
    level_ = level;
  }
  
  // Create a new node to insert next.
  next = NewNode(level, key, value);
  // Update the pointer of the node layer by layer and insert it layer by layer
  for (int j = 0; j < level; ++j) {
    next->SetNext(j, prev[j]->Next(j)); // The node in the levelJ layer of the node points to the node in the levelJ layer linked list of prev (hop position)
    prev[j]->SetNext(j, next); // Pointing the level J layer list of the pre jump point to the level J layer list node of Next
  }
  
    return true;
}

The number of layers generated by random Level () in the above code is the total number of layers of the jump table. It also represents the number of layers of the new node. For example, in Figure 3.2, the node key=3, the height is 1, the key=6, and the height is 4.

Random Level Random Layer Generation
setNext Sets the Link List of Nodes

Lookup operation

The first step in the insertion operation is our lookup operation. Instead of parsing, we encapsulate a layer of code directly.

template <typename Key, typename Value>
Value
SkipList<Key, Value>::Find(const Key &key) {
  Node* node = FindGreaterOrEqual(key, NULL);
  if (node) {
    return node->value;
  }
  return NULL;
}

Delete operation

In Level deb, SkipList is not deleted. Level db's jump table is only used to increase the number of query nodes. If you want to delete a node, you just mark a node as deletion, because the deletion operation has to recalculate the level levels and update the list of nodes in each layer, which is too performance-consuming.

But here we still implement the deletion of the jump table. Similarly, the deletion and insertion of the jump table are the same.

1. Find the node that needs to be deleted first
2. If the node is found, the pointer field is updated, and the level needs to be updated, each linked list is updated layer by layer.

template <typename Key, typename Value>
bool
SkipList<Key, Value>::Delete(const Key&key)
{
  Node* prev[kMaxLevel];
  Node* next = FindGreaterOrEqual(key, prev);

  int level = level_;
  if (next && next->key == key) {
    // Set the hop list for each layer to the list for each layer that the next node points to
    for (int i = 0; i < level; ++i) {
      if (prev[i]->Next(i) && prev[i]->Next(i)->key == next->key) {
        prev[i]->SetNext(i, next->Next(i));
      }
    }

    // Release all memory in the node array
    free(next);

    //If the largest node is deleted, the jump table needs to be re-maintained
    for (int j = level_-1; j >= 0 ; --j) {
      if (head_->Next(j) == NULL) {
        level_--;
      }
    }
    return true;
  }

  return false;
};

Figure 4.1

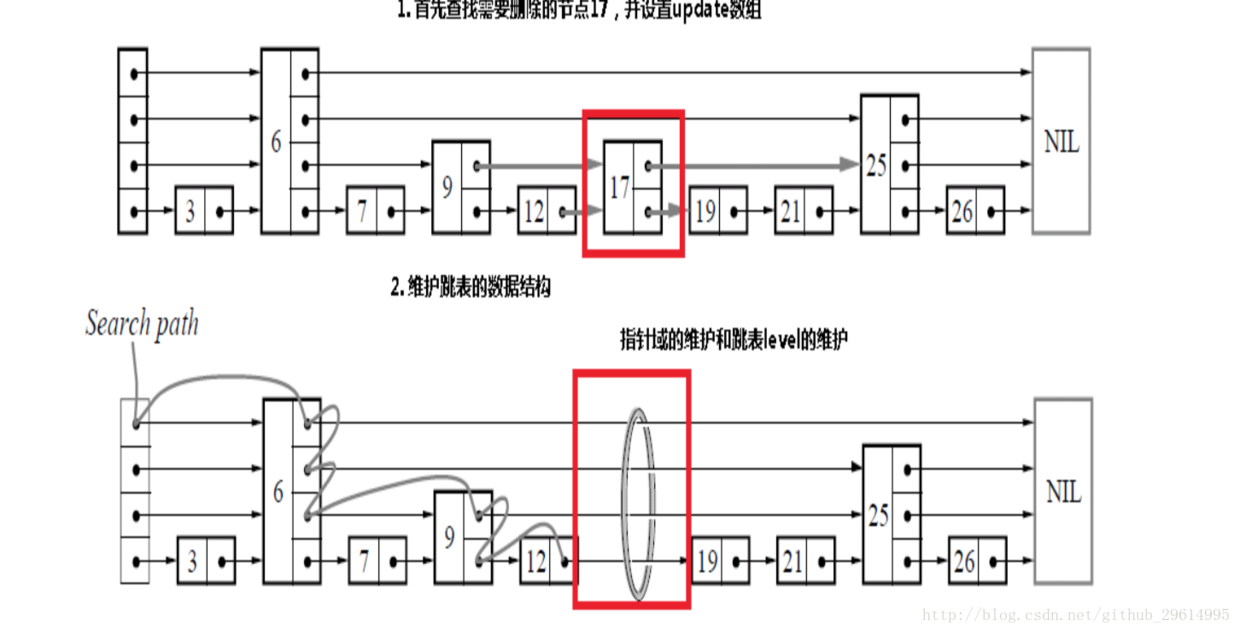
As shown in Figure 4.1, delete the operation when the node key=17, first find and return to the next node, check whether the next node is key=17, and if so, update all the hops layer by layer, and update the number of layers.

Affiliated Implementation Code

Generating Node Method

template <typename Key, typename Value>
typename SkipList<Key, Value>::Node*
SkipList<Key, Value>::NewNode(int level, const Key& key,  const Value& value)
{
  size_t men = sizeof(Node) + level * sizeof(Node*);
  Node* node = (Node*)malloc(men);
  node->key = key;
  node->value = value;
  return node;
}

In the code, sizeof(Node) allocates memory for its own structure, and level * sizeof(Node *) allocates memory for forward_array, because it allocates level node lists. In leveldb, byte alignment is used to allocate this memory. I haven't written it out here. If you are interested, you can browse the source code.

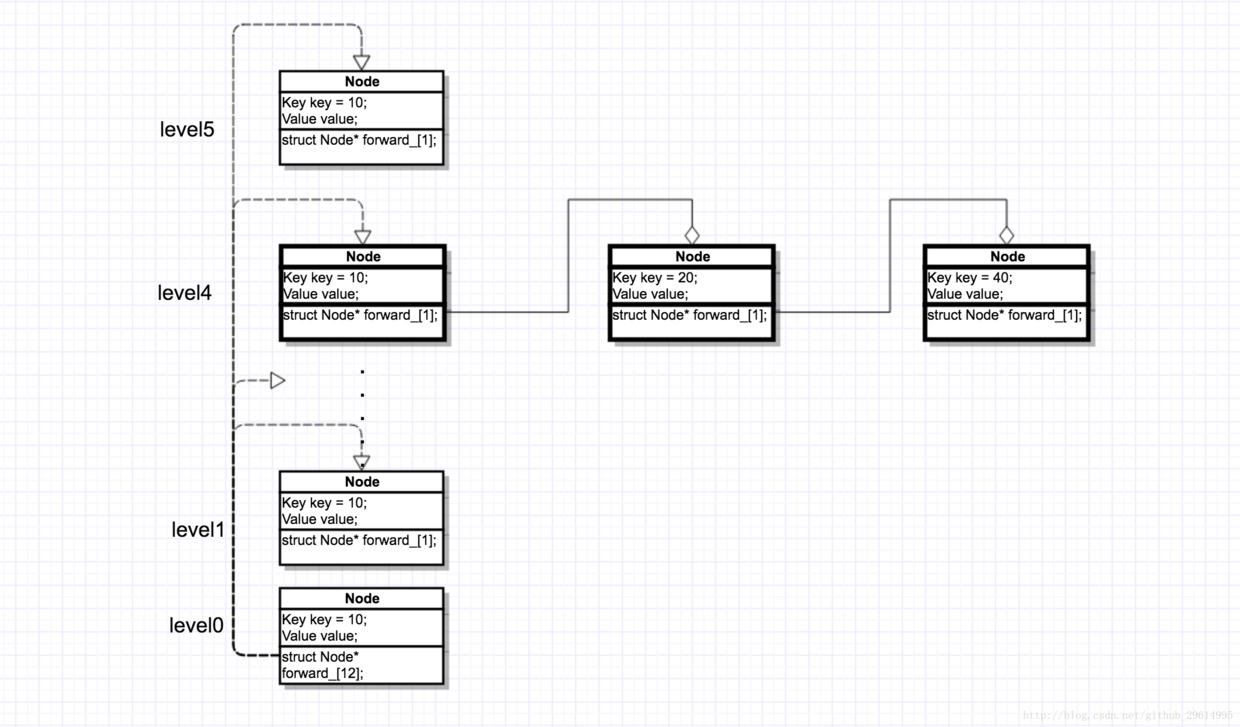
Let's assume level = 4

Figure 6.1

The code generates the structure of Figure 6.1. The forward_array size of level0 node is 4. Both leve1 and level3 are empty nodes, but 8 bytes of pointer memory (64-bit operating system) are allocated. The dotted lines in the graph are represented by array references, not pointers.

Implementation of Random Layer Generating Number Method

Implementation of Level dB from google Open Source Project

template <typename Key, typename Value>
int SkipList<Key, Value>::randomLevel() {

  static const unsigned int kBranching = 4;
  int height = 1;
  while (height < kMaxLevel && ((::Next(rnd_) % kBranching) == 0)) {
    height++;
  }
  assert(height > 0);
  assert(height <= kMaxLevel);
  return height;
}

uint32_t Next( uint32_t& seed) {
  seed = seed & 0x7fffffffu; // Avoid negative numbers

  if (seed == 0 || seed == 2147483647L) { 
    seed = 1;
  }

  static const uint32_t M = 2147483647L;   // 2^31-1
  static const uint64_t A = 16807;  // bits 14, 8, 7, 5, 2, 1, 0
  // We are computing
  //       seed_ = (seed_ * A) % M,    where M = 2^31-1
  //
  // seed_ must not be zero or M, or else all subsequent computed values
  // will be zero or M respectively.  For all other values, seed_ will end
  // up cycling through every number in [1,M-1]
  uint64_t product = seed * A;

  // Compute (product % M) using the fact that ((x << 31) % M) == x.
  seed = static_cast<uint32_t>((product >> 31) + (product & M));
  // The first reduction may overflow by 1 bit, so we may need to
  // repeat.  mod == M is not possible; using > allows the faster
  // sign-bit-based test.
  if (seed > M) {
    seed -= M;
  }
  return seed;
}

Generally speaking, the method of generating level layers is not random. The number of layers is determined by the number of times seed is constantly modified. In other words, the number of level 0 nodes determines the number of layers.

Method Implementation of Node Structures

template <typename Key, typename Value>
void 
SkipList<Key, Value>::SetNext(int i, Node* x) {
    assert(i >= 0);
    forward_[i] = x; // Setting Array Nodes
}

template <typename Key, typename Value>
void 
SkipList<Key, Value>::Node* Next(int i) {
    assert(i >= 0);
    return forward_[i];
}

The SetNext(int i, Node* x) method is to set a list reference at level I of the forward_node array.
For example, in Figure 6.1, key=10 calls the expressions of SetNext (4, Node where key=20 and level = 4) and key=20 calls SetNext(4, Node where key = 40 and level = 4).

Figure 6.2

Next(int i) is a method of extracting a link list of nodes at a certain level. This should not be resolved.

Output Jump Table Structure

template <typename Key, typename Value>
void
SkipList<Key, Value>::Print()
{
  Node* next, *x = head_;

  printf("--------\n");
  for (int i = level_ - 1; i >= 0; --i) {
    x = head_;
    while ((next = x->Next(i))) {
      x = next;
      std::cout << "key: " << next->key << " -> ";
    }
    printf("\n");
  }
  printf("--------\n");
}

Print method output to see which node structure the current jump table has

Source code download

<br />
<br />
<br />

Reference material:

SkipList
Detailed Explanation and Implementation of Skip List Principle