Light out problem (poj 1222) - difficult
http://poj.org/problem?id=1222
Problem Description:
There is a matrix composed of buttons, in which there are 6 buttons in each row, a total of 5 rows. There is a light on the position of each button. When a button is pressed, the button and the lights in the surrounding positions (upper, lower, left and right) will change once. That is, if the lamp is turned on, it will be turned off; If the lamp was turned off, it will be turned on. The button at the corner of the matrix changes the state of three lights; The button on the edge of the matrix changes the state of 4 lights; Other buttons change the state of the five lights.
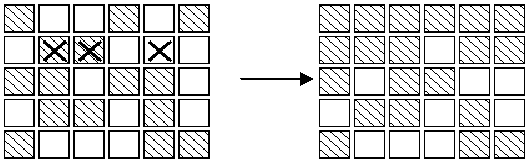
In the above figure, the button marked with X in the matrix on the left represents being pressed, and the matrix on the right represents the change of lamp state. Set an initial state for each lamp in the matrix. Please press the button until each lamp goes out. When multiple buttons adjacent to a lamp are pressed, one operation will offset the result of another operation. In the figure below, the buttons in Row 2, column 3 and column 5 are pressed, so the state of the lights in Row 2 and column 4 will not change.
Please write a program to determine which buttons need to be pressed to just turn off all the lights. According to the above rules, we know that 1) pressing the same button for the second time will cancel the result of the first press. Therefore, each button only needs to be pressed once at most; 2) The order in which each button is pressed has no effect on the final result; 3) For each light in the first row, press the corresponding button in the second row to turn off all the lights in the first row. If this is repeated, all the lights in rows 1, 2, 3 and 4 can be turned off. Similarly, press the buttons in columns 1, 2, 3, 4 and 5 to turn off the lights in the first five columns.
Input: composed of 5 lines, each line includes 6 numbers (0 or 1). Two adjacent numbers are separated by a single space. 0 indicates that the initial state of the lamp is off, and 1 indicates that the initial state of the lamp is on.
Output: composed of 5 lines, each line includes 6 numbers (0 or 1). Two adjacent numbers are separated by a single space. Where 1 indicates that the corresponding button needs to be pressed, and 0 indicates that the corresponding button does not need to be pressed.
Input sample:
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
Output example:
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
Idea: first of all, each lamp actually has only two states, either on or off. And the light returns to its original state without pressing it twice. The first idea is to enumerate the corresponding states for each lamp, and finally judge whether it meets the conditions. However, if there are 30 lamps in total, it is necessary to enumerate the number to the 30th power of 2. It is too large, so now we must find a way to reduce the number of enumerations.
So how do we reduce complexity? The answer is to use local. If the part is determined, then all the remaining cases are also determined, or there are only n kinds that are not a few. Therefore, in the process of enumeration, it is good to enumerate the part. In this topic, the part is the first line. As long as the first line is determined, if the second line must be turned off, it can only be "inserted", because if it is not inserted empty, the lights originally turned off in the first line will be turned on again. In short, when enumerating the first row, some of the lights in the first row are on and some are dark. In order to turn off the lights in the first row, we can only use the lights in the second row. The following lines are followed by analogy. At the last line, judge whether all have been extinguished.
Then there is the problem of storage. Generally speaking, it is stored in a two-dimensional array. One method learned in this problem is to store in binary, because the matrix has only two arrays of 0 and 1. If I use a two-dimensional array, I need to use 30 int s. If I use binary storage, I just need to use a one-dimensional array of char, Because eight bits in one space is enough. But if it is stored in this way, it is necessary to be very familiar with bit operation.
Another point is the traversal of the newly learned bit operation. It needs to traverse a total of 6 bits. As long as you subtract one from the 6th power of 1 to 2, you can traverse all the possibilities. If this is not the case, we need to design six cycles, each of which is 0 and 1
code:
1 #include <memory>
2 #include <string>
3 #include <cstring>
4 #include <iostream>
5 using namespace std;
6 char orilights[5];
7 char lights[5];
8 char result[5];
9 int GetBit(char c,int i ){
10 //This function is to get c The first i Digit number
11 return (c >> i ) & 1 ;//c Shift right i And then with 1
12 //1 In fact, it is 00000 1, and everything else is 0, so the sum operation will not change the bits except the first bit
13
14 }
15 void SetBit(char &c, int i , int v){
16 //This function is used to set whether the value of a bit is 0 or 1
17 if(v){
18 c |= ( 1 << i );
19 }else{
20 c &= ~( i << i );
21 //As long as you are familiar with these two bit operations
22 }
23 }
24
25 void FlipBit (char c,int i){
26 //This function is used to invert bits
27 // XOR operation
28 //XOR with 1 remains unchanged and XOR with 0 reverses
29 c ^= (1 << i );
30 }
31
32
33 void OutPutResult(int t,char result[]){
34 cout<<"Puzzle #"<<t<<endl;
35 //Switch matrix
36 for(int i = 0;i<5;i++){
37 for(int j = 0;j<6;j++){P
38 cout<<GetBit(result[i],j);
39 if(j<5){
40 cout<<" ";
41 }
42 }
43 cout<<endl;
44 }
45 }
46 int main(){
47 int T;
48 cin>>T;
49 for(int t = 1;t<T;t++){
50 for(int i = 0;i<5;i++){
51 for(int j = 0;j<6;j++){
52 int s;
53 cin>>s;
54 SetBit(orilights[i],j,s);
55 }
56 }
//In fact, the above is to read each bit into the array. Is each design 1 or 0
57 for(int n = 0;n<64;n++){
//Here is the enumeration of bit operations mentioned above. The value should be 63
58 int switchs = n;
59 memcpy(lights,orilights,sizeof(orilights));//This function is used to assign the binary of orilights to lights, which is copied directly in memory
60 //This function is direct cpy Binary value
61 for(int i = 0;i<5;++i){
62 result[i] = switchs;
//Every time a line is processed, the switches of the previous line should be saved in the result
63 for(int j = 0;j<6;j++){
64 if(GetBit(switchs,j)){//Get the number at the j-th position of this number
65 if(j>0){//Not the leftmost number
66 FlipBit(lights[i],j-1);
67 }
68 FlipBit(lights[i],j);
69 if(j<5){//Not the rightmost number
70 FlipBit(lights[i],j+1);
71 }
72 }
73 if(i<4){
//All the current lines have been processed before. Now it's time to process the next line
//This is still very clever. Just use an XOR. As long as the first line is 1, turn off the light in the first line. If it is 0, i keep it as it is
74 lights[i+1] ^= switchs;
75 }
76 switchs = lights[i];
77 }
78 if(lights[4]==0){
79 //All gone
80 OutPutResult(t,result);
81 break;
82 }
83 }
84 }
85 }
86 return 0;
87 }
88
Conclusion: first of all, if you want to finish this problem with bit operation, you must be very familiar with bit operation. Also be able to traverse bit operations and be very familiar with the optimization of enumeration. I have to look at the latter question myself.