Linear algebra and code implementation (I) vector

background

The Linear Algebra I studied in university is a little forgotten now, and I am not proficient in the code implementation; This column mainly reviews the basis of linear algebra and implements the code part;

1. Some basic concepts

Essence: the basic expression of a group of numbers and the basic elements of linear algebra;

The starting point of introducing vector: give the value the attribute of direction;

An important role: represent N-dimensional data (in real life, data is often multi-dimensional)

2. Code implementation simple vector class

class Vector:
    def __init__(self, array):
        self._value = list(array)		# list is used here to assign values to objects and prevent objects from being modified outside the class
    
    # Index one of the elements
    def __getitem__(self, index):
        return self._value[index]
    
    # Return vector length
    def __len__(self):
        return len(self._value)
    
    def __repr__(self):
        return "Vector({})".format(self._value)		# Called when the system prints a vector
    
    def __str__(self):
        return "({})".format(", ".join(str(a) for a in self._value))	# Called when using print

Because the array can well represent the vector, the implementation of the vector is some operations on the data;

3. Implementation of vector addition operation

def __add__(self, other):
	assert len(self) == len(other), \
		"Error in adding. len of vecters is not same"
	return Vector([a + b for a, b in zip(self, other)])		# Here zip in the iterator object

# Turns a vector into an iteratable object
def __iter__(self):
    return self._value.__iter__()

The subtraction operation of vector is similar to addition, which only needs to modify the symbol;

4. Zero vector

Definition: for any vector V, there is a vector O, which satisfies: v + O = v

Code implementation:

# Define a class method
@classmethod
def zero(cls, n):
	return cls([0] * n)

5. Length of vector

It seems to be university knowledge, called the module of vector, which is actually the calculation method of Euler distance;

Unit vector: the module length is 1, the direction is consistent with the original vector, indicating the direction, which is called the normalization and normalization process;

The following is the code implementation:

import math

# Find the module of vector
def norm(self):
	return math.sqrt(sum(e**2 for e in self))

# Find the unit vector of the current vector
def normal_one(self):
	return 1 / self.norm() * Vector(self._value)

6. Dot multiplication of vectors

Implementation formula:

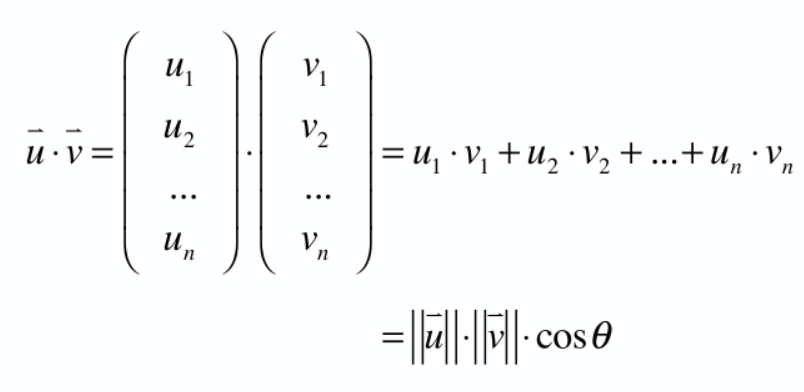
In fact, it is easy to understand. It can be understood as mapping one vector to another, or decomposing two vectors into x-axis and y-axis and multiplying them;

According to the geometric meaning, the following conclusions can be well drawn:

The multiplication of two vector points is equal to 0, and the included angle is 90 °;

The multiplication of two vector points is greater than 0, and the included angle is less than 90 °;

The multiplication of two vector points is less than 0, and the included angle is greater than 90 °;

The point multiplication of vectors can actually judge the similarity of two vectors, that is, in the application of recommendation system;

Code implementation:

def dot(self, other):
	assert len(self) == len(other), \
		"Error in adding. len of vecters is not same"
	return Vector([a * b for a, b in zip(self, other)])		# Here zip in the iterator object

7. Use of vectors in Numpy

# Define a vector
vec = np.array([1, 2, 3])		
print(np.zeros(5))
print(np.ones(5))
print(np.full(5, 666))

# numpy basic operation
vec2 = np.array([4, 5, 6])
print("{} + {} = {}".format(vec, vec2, vec + vec2))
print("{} - {} = {}".format(vec, vec2, vec - vec2))
print("{} * {} = {}".format(2, vec, 2 * vec))
print("{} * {} = {}".format(vec, vec2, vec * vec2))
print("{}.dot({}) = {}".format(vec, vec2, vec.dot(vec2)))

print(np.linalg.norm(vec))
print(vec / np.linalg.norm(vec))
print(np.linalg.norm(vec / np.linalg.norm(vec)))

As the most commonly used library, Numpy contains all methods for vector processing. Its internal implementation is just like our own implementation, which is only encapsulated, and we can call it directly in practical engineering; Vector is only the simplest application. In fact, when processing some data (especially images), it is often in the form of matrix, which is more complex than vector. The next part will explain the knowledge of matrix and code implementation;