🎆 Understand sequential stack and chain stack
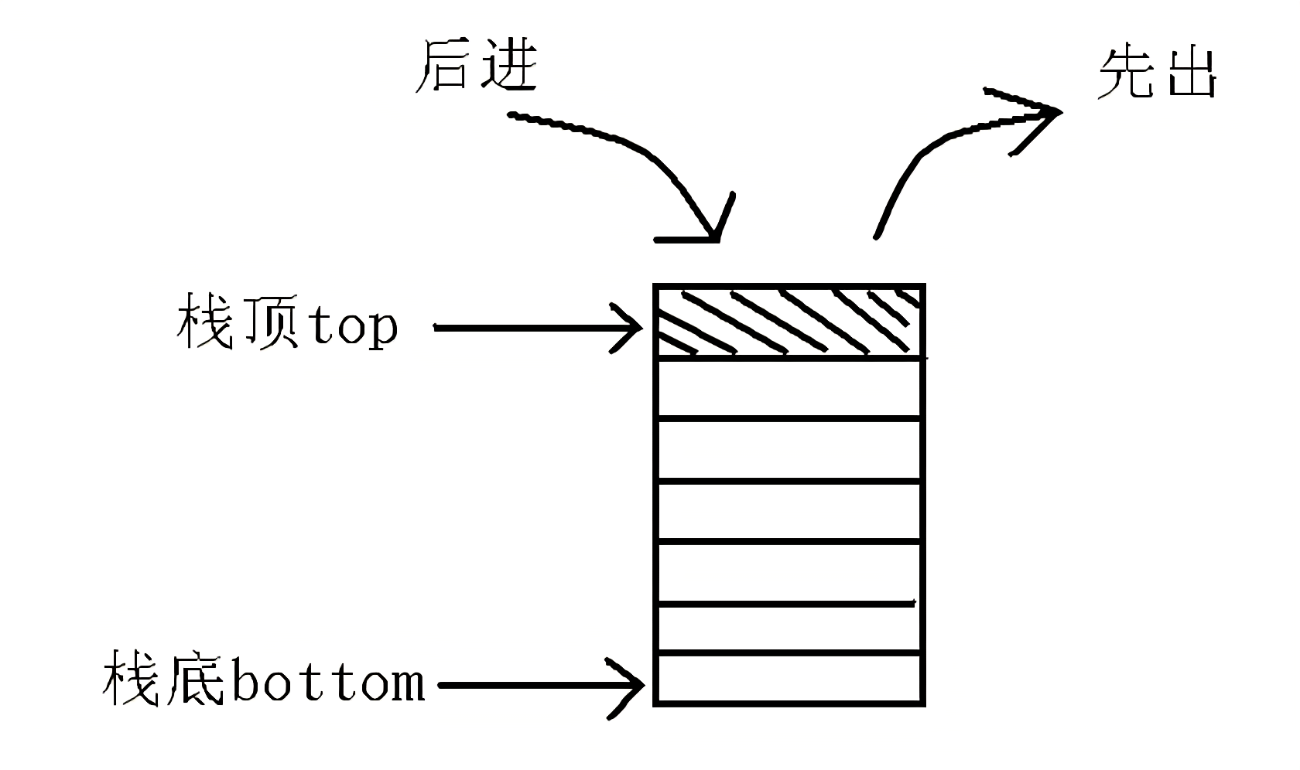
- In the world of data structure, stack, like sequential list and linked list (linked storage structure), is a linear storage structure. Stack is a linear table (logical structure concept) with limited operation. The particularity of its operation lies in its "last in, first out" characteristic. For example, you keep putting plates on the table, and when you take these plates, you can only start with the top plate you just put in.
- The Top of each disk release is called the Top of the stack, which is the end of the linear table that allows insertion and deletion.
- The Bottom plate is called the Bottom of the stack, that is, the other end where insertion and deletion are not allowed.
- The bottom of the stack is fixed and the top of the stack is floating. When the number of elements in the stack is zero, the stack is called an empty stack. The operation of inserting is generally called push ing, while the operation of deleting (extracting specified elements from the stack) is called pop.
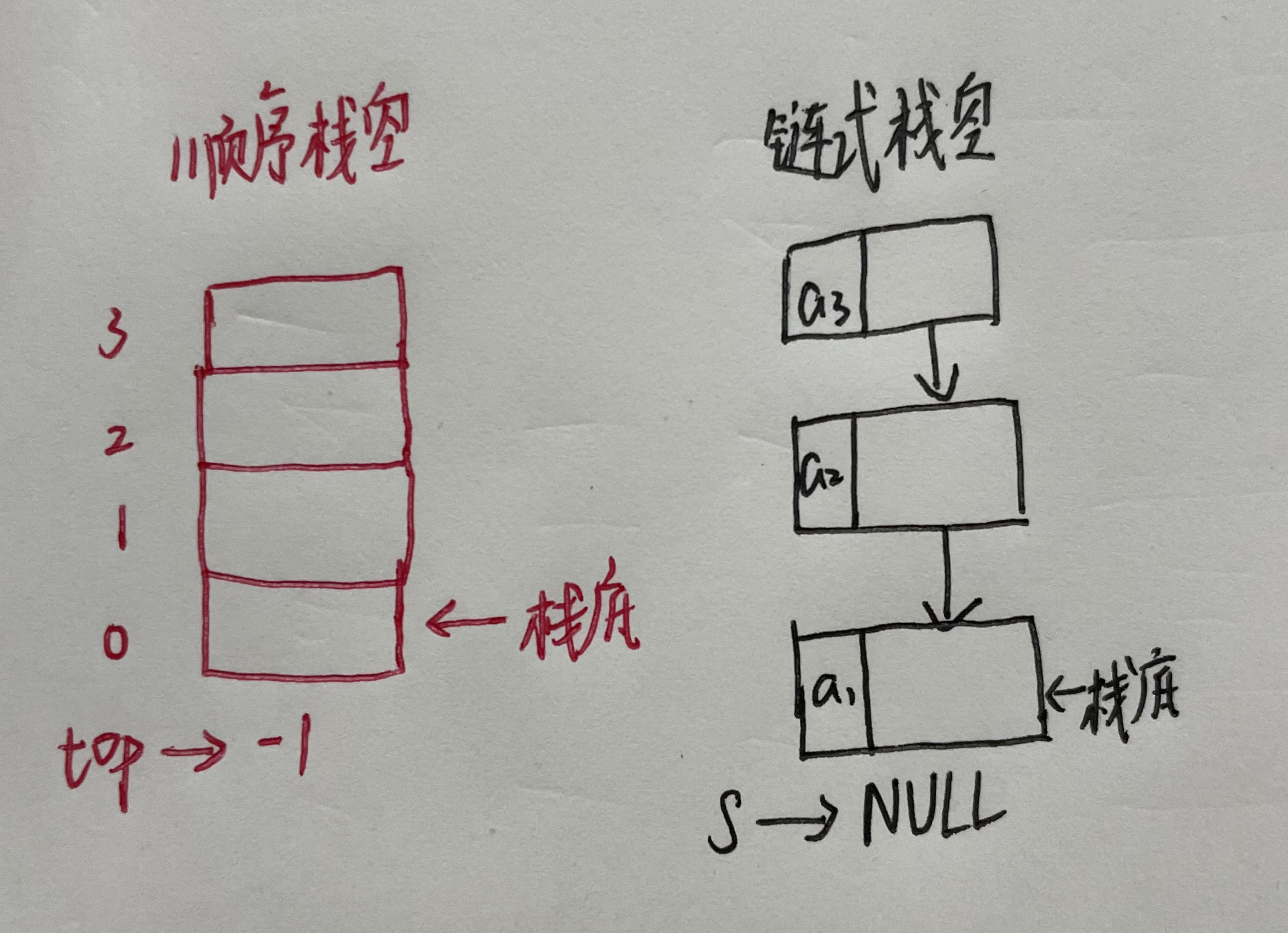
Now I'm introducing two ways to implement the stack. As we all know, all data structures are closely related to linked lists and arrays. And so is the stack. The stack using sequential storage is called sequential stack, which uses array to store its data from the bottom of the stack to the top of the stack. The chain stack is realized with the help of the linked list. We usually take the head of the linked list as the top of the stack and the tail as the bottom of the stack.
🎆 Initialization and establishment of stack
👇 Sequential stack
- First, we introduce the initialization of sequential stack and simple related operations. We need to understand several key points before we start to look at the code.
- 1. The sequence stack is a structure, which consists of an int type variable and an array storing a certain data type.
#define MAXsize 20 / / the maximum element in the stack
typedef int Elemtype;//Common data element type definitions in data structures
//[ 👇] The following is the definition of sequential stack
typedef struct odstack {
Elemtype data[MAXsize];
int top;//Top is the stack top pointer (indicating the subscript of the current stack top element)
}ODstack;
- 2. When you see the variable top in the code, it is the stack top pointer of the stack (top represents the subscript of the current stack top element)
- 3. Introduce three simple operations for sequence (initialization stack, stack entry and stack exit)
- 4. Because data [maxsize] starts with subscript 0, S1 - > Top = - 1 means that the stack is empty, and S1 - > Top = maxsize-1 means that the stack is full.
- 5. Initialization: the top value in the stack is equal to - 1
- 6. Stack pressing: to judge whether the stack is full, do not add 1 to top first and then enter the stack
- 7. Out of stack: determine whether the stack is empty. Instead, first out of the stack and then top-1
Let's look at the code implementation 👇👇👇👇👇👇👇
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define MAXsize 20 / / the maximum element in the stack
typedef int Elemtype;//Common data element type definitions in data structures
//[ 👇] The following is the definition of sequential stack
typedef struct odstack {
Elemtype data[MAXsize];
int top;//Top is the stack top pointer (indicating the subscript of the current stack top element)
}ODstack;
//Stack initialization[ 👇]
bool initODstack(ODstack* s1) {
s1->top = -1;
return true;
}//Let the stack top pointer be - 1 first
//Stack[ 👇]
bool push(ODstack* s1,Elemtype newdata) {//newdata is the new element to be pushed into the stack
if (MAXsize-1==s1->top) return false;
else s1->data[++s1->top]=newdata;
return true;
}
//Out of stack[ 👇]
bool pop(ODstack* s1,Elemtype *outdata) {//outdata is the element out of the stack (use a pointer so that this number can be expressed outside the function)
if (-1 == s1->top)return false;
else *outdata = s1->data[s1->top--];
return true;
}
int main(void) {
ODstack s1;
initODstack(&s1);
int i;
for (i = 0;i < 6;i++) {
int newdata;
scanf("%d", &newdata);
push(&s1, newdata);
}
int length = s1.top;
for (i = 0;i <= length;i++) {
Elemtype *outdata=(int*)malloc(sizeof(ODstack));
pop(&s1, outdata);
printf("The top layer is:%d\n", *outdata);
}
}
👇 Chain stack
- After a brief understanding of the operation of the sequential stack, let's take a look at the related simple operations of the chained stack. The general idea of the chained stack is the same as that of the sequential stack, except that it takes the head of the linked list as the top of the stack and the tail of the linked list as the bottom of the stack.
- So how do we put and put the chain stack into and out of the stack? Putting the data into the stack is to insert the data from the head of the linked list, and putting the data out of the stack is to delete the first node of the head of the linked list.
- So what's special about the chain stack compared with the sequential stack? 1. No head node is required. 2. Because the length of the chain list is dynamic, the chain stack is basically not full. 3. The head pointer is the top of the stack, and an empty stack is equivalent to the head pointer pointing to null.
- Now let's look at all the related operations of the chained stack 👇👇👇👇
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
//[definition of chain stack 👇]
typedef struct linkstack {
int data;
struct linkstack* next;
}LINKstack;//Define a chained stack (the restricted first in first out rule makes it essentially different from the linked list)
//[initialization of chain stack] 👇] Similar to sequential stack
LINKstack* initstack(LINKstack* s) {
s = NULL;
return s;
}
//[judge whether it is an empty stack 👇]
bool emptystack(LINKstack* s) {
if (s)return true;
else return false;
}
- The judgment condition for an empty stack is similar
- Stack in and stack out 👇
//[operation of chain stack] 👇]
LINKstack* push(LINKstack* s, Elemtype newnum) {
LINKstack* newstack=(LINKstack*)malloc(sizeof(LINKstack));
newstack->data = newnum;
newstack->next = s;
s = newstack;
return s;
}
//[out of chain stack] 👇]
LINKstack* pop(LINKstack* s,Elemtype *newnum) {
if (s==NULL) {
printf("Stack is empty");
return NULL;
}
else {
*newnum = s->data;
LINKstack* p = s;
s = s->next;
free(p);
return s;
}
}
🎆 Application scope of stack
- After a simple understanding of the stack, under what circumstances will we use the stack structure?
- The stack can store breakpoints when a function is called, and it will play a great role when a function is recursive.
- The fallback function in the upper left corner of the browser, which is often used to surf the Internet in our daily life, uses the stack storage structure at the bottom.
- Bracket matching problem (check whether the parentheses of your program are correct in the compiler) is also implemented by stack structure.
- Binary conversion, expression evaluation, reverse output, etc

🎇 Simply solve the problem with the stack - (valid parentheses)
- Two months ago, there was a topic on force buckle, that is, the bracket matching problem we mentioned, which was applied to the stack method. Now let's have a deeper understanding of the stack method through specific examples
✨ Simple loop implementation
- For this problem, if we haven't learned about stack before, it can also be solved. First, you need to observe the examples yourself, or you can write longer valid parentheses to find the rules.
- You can find that there must be a corresponding right parenthesis to the right of the last left parenthesis. At the same time, we can define an array to store the left parentheses that have not been matched before, and the following right parentheses to judge. (the whole logic is equivalent to using loops and arrays to simulate the idea of a stack)
- The code is as follows 👇👇
bool isValid(char * s){
if(strlen(s)%2==1)return false;//If it's an odd number, it's obviously a direct error
char l[10000],r[10000];
int i=0,j=0,left=0;//j is the subscript of the array in the right parenthesis (if it matches, j must be equal to left in the end)
while(*s!='\0')//Three judgment statements are used for classification
{
if(*s=='('||*s=='{'||*s=='[')
{
l[++i]=*s;
left++;//Count the number of left parentheses
}
else if(*s==')')
{
r[j]='(';
if(r[j]!=l[i])
return false;
j++;
i--;
}
else if(*s=='}')
{
r[j]='{';
if(r[j]!=l[i])
return false;
j++;
i--;
}else if (*s==']')
{
r[j]='[';
if(r[j]!=l[i])
return false;
j++;
i--;
}
s++;
}
if(j!=left)return false;//The number of left and right parentheses is not equal
return true;
}
✨ Using stack method to solve
- Using the stack to solve this problem is the most commonly used and best understood method. In the previous cycle, we have unconsciously touched the stack solution. Now we use the stack to write it more accurately.
- First of all, let's take a look at a picture selected from the official answer of Li Kou, which clearly shows the operation process of stack on this problem.
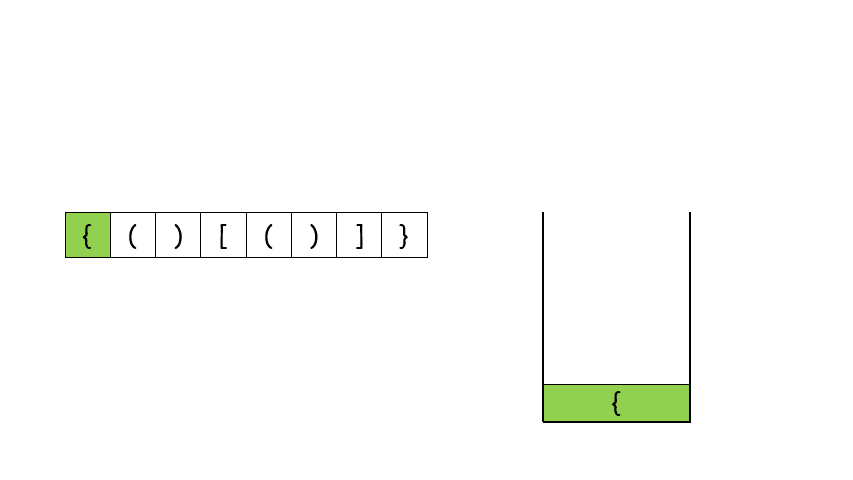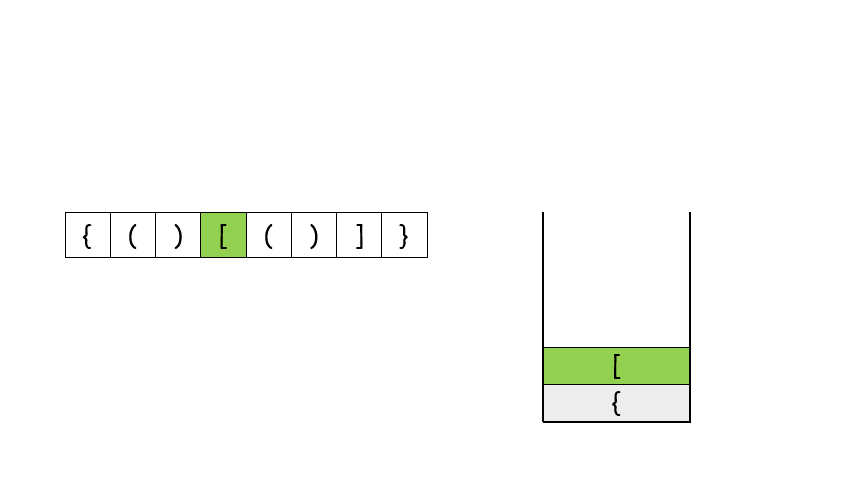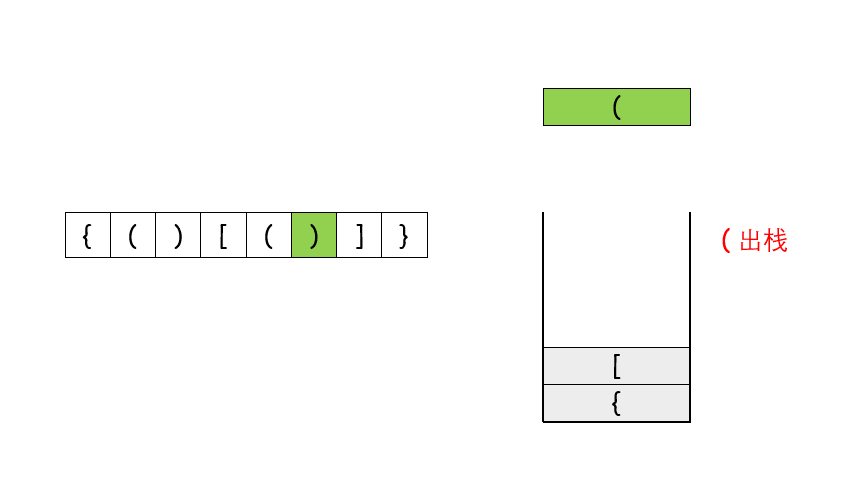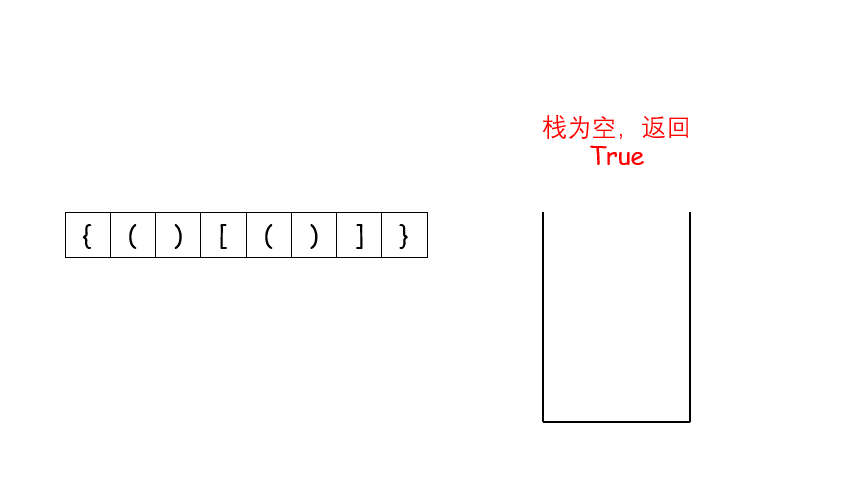
- Let's look at the code 👇👇👇
char reversech(char s){
if(s==')')return '(';
else if(s=='}')return '{';
else if(s==']')return '[';
return 0;
}//Because the right bracket is compared with the left bracket, a function to reverse the character is defined
bool isValid(char * s){
int n =strlen(s);
if(n%2!=0)return false;//Direct exclusion under special circumstances
int i=0;
char stack[n+1];//Define stack (char type)
int top=-1;//Stack top pointer (initialization point to - 1)
for(i=0;i<n;i++){
if(s[i]=='('||s[i]=='{'||s[i]=='['){
stack[++top]=s[i];//The left parenthesis fills the stack with parentheses
}else{
if(top==-1||stack[top]!=reversech(s[i])) return false;//If the stack is empty and there are closing parentheses, an error occurs.
//The last left parenthesis is not equal to the right parenthesis, and it is also a direct error
top--;//If the first two don't jump out, top -- (change the stack top pointer to simulate the stack)
}
}
return top==-1;//(the end stack is empty)
}
✨ Longest valid bracket
- Through the above application of stack, we must have a direction for this data structure, so we will increase the difficulty on the basis of the previous question. Let's look for the longest valid parenthesis in the whole string of parentheses.

Let's focus on some key points first - First, valid parentheses must start with an open parenthesis
- By analyzing several special cases, when we encounter such brackets () (), we find that if we directly find a whole valid bracket (until it is found to be invalid) is wrong, it may be wrong when we encounter such situations as () (). What do you mean, we do not directly find this 4, but carry out the operation of 2 + 2.
- How to calculate the length of the current valid bracket? Whether to define a curlength=0 self increment or subscript subtraction.
Let's look at the code 👇👇👇
int longestValidParentheses(char * s){
if(!s)return 0;
int length=strlen(s);
int stack[length+1];//In the following text, it is used to record the length of this valid bracket (store the subscript at the beginning of the valid bracket)
int max=0;//Store the longest valid bracket
int top=-1;//Stack top pointer
int curlength=0;//Length of currently valid parentheses
stack[++top]=-1;//++top is because - 1 cannot be subscript. Why is it - 1 (example: () () () subscript: 0 1 2 3? Because the existence of 0, the head minus tail is not equal to the length
//So move one bit back.
for(int i=0;i<length;i++){
if(s[i]=='('){//Left parenthesis
stack[++top]=i;//Stack to store the subscript of the current bracket
}else{//Right parenthesis (two possibilities: 1. The stack is empty (the first one is the right parenthesis, which must be wrong) 2. It matches an left parenthesis in the stack)
--top;//First, self subtract the stack top pointer
if(top==-1){//If it is satisfied, it means that the original stack is empty (the first case)
stack[++top]=i;//
}else{
curlength=i-stack[top];//The length of this valid bracket
if(curlength>max)max=curlength;
}
}
}
return max;
}
In addition to this method, there is another conversion idea of the problem. Still use an array to store the subscripts of no stacked elements. If the left bracket matches successfully, set it to 1. Finally, set the remaining left bracket or right bracket to 0. Then the problem becomes the problem of finding the longest continuous 1, which is much easier to solve.
🥇 Write at the end
- There are many problems about stack, and stack is widely used. If you want to improve the writing ability in this regard, you still need to brush a lot of questions and expand your knowledge.