Intersection of two unidirectional linked lists
Problem Description:
There are two one-way linked lists. They may or may not intersect. If it intersects, it returns the intersecting node; if it does not intersect, it returns null.
There are only three cases when two one-way linked lists intersect.
The problem of linked list intersection is one of the most difficult problems in the linked list problem!!!!
1, Analyze three situations one by one
[case 1] two linked lists
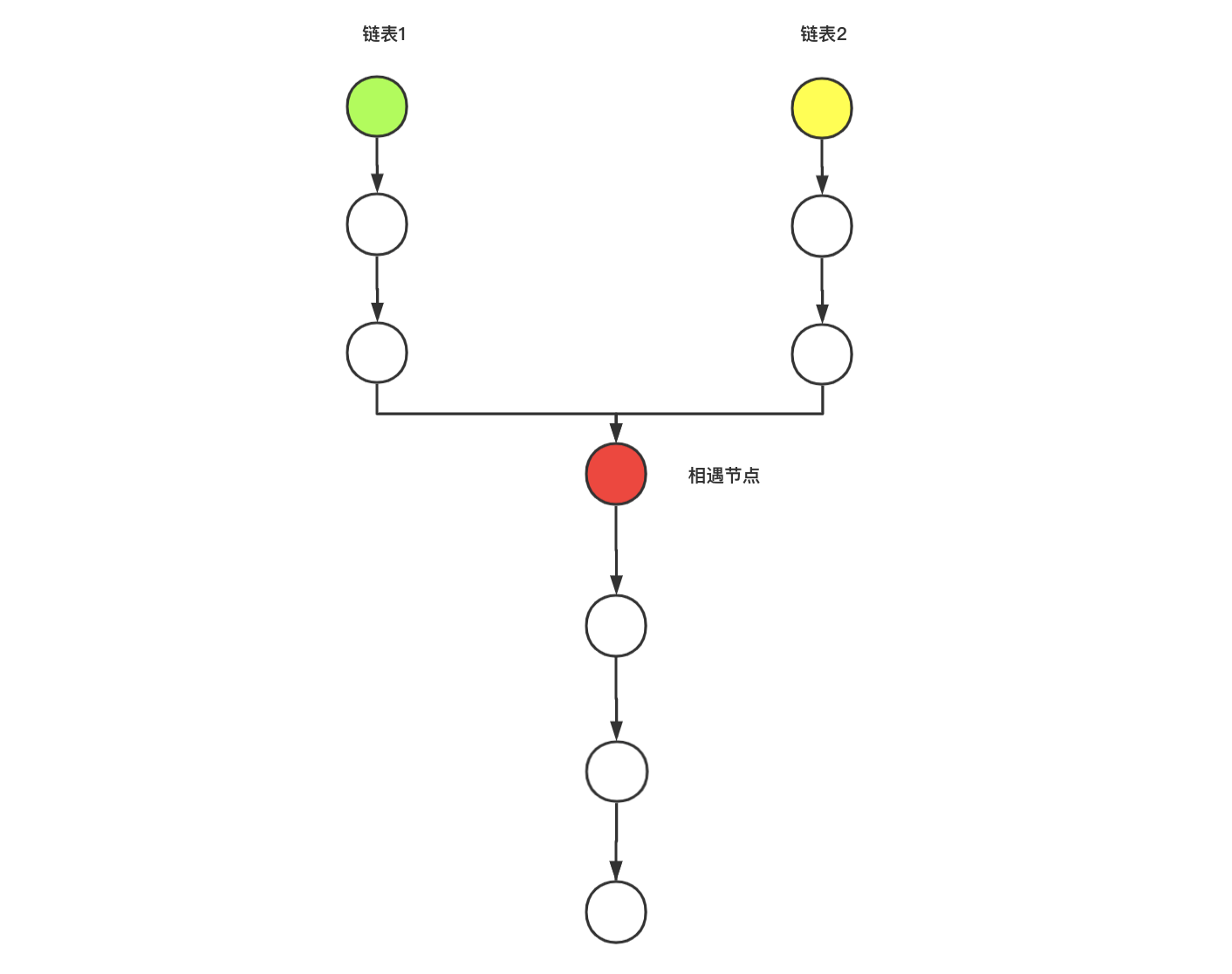
Method 1: do it through hash table
Implementation process:
- First, traverse a linked list from beginning to end, and put the nodes into the hash table at the same time
- Then traverse the second linked list from beginning to end. While traversing, first check whether there is this node in the hash table
- If yes, it proves that the node has been added to the first linked list, indicating that the node is a common node (intersecting node) of the two linked lists. Just return to the node immediately
- Until the second linked list is traversed, and no duplicate node is found in the hash table, it indicates that the two linked lists do not intersect
The code implementation is as follows:
public static SingleNode findFistIntersectNode01(SingleNode head1, SingleNode head2) {
if (head1 == null || head2 == null) {
return null;
}
final HashSet<SingleNode> set = new HashSet<>();
// First select a linked list and add all nodes of the linked list to the hash table
while (head1 != null) {
set.add(head1);
head1 = head1.next;
}
// Traversing the second linked list, each node traversed will go to the set set to check whether the node has been added. If so, the node is the intersection node of the two linked lists
while (head2 != null) {
if (set.contains(head2)) {
return head2;
}
head2 = head2.next;
}
// If the second linked list is traversed and the same node is not found in the set set, the two linked lists do not intersect
return null;
}
node definition
@Data
public class SingleNode<T> {
public T value;
public SingleNode next;
public SingleNode() {}
public SingleNode(final T data) {
this.value = data;
}
@Override
public boolean equals(final Object o) {
if (this == o) return true;
if (o == null || this.getClass() != o.getClass()) return false;
final SingleNode that = (SingleNode) o;
return Objects.equals(this.value, that.value);
}
@Override
public int hashCode() {
return Objects.hash(this.value);
}
@Override
public String toString() {
return (String) this.value;
}
}
Method 2. Do it by traversing two linked lists
Implementation process:
- By first traversing the length of the two linked lists, and then taking the last node of each linked list, compare whether the two nodes are equal. If they are equal, they intersect, otherwise they do not intersect.
- If they intersect, subtract the length of the short list from the length of the long list, and then take the difference step first.
- Then the short linked list starts from the chain header, and the long linked list continues to go until the memory address of the node they go to is the same, and the node is the node they intersect.
/**
* @param head1 The head node of the first linked list
* @param head2 The head node of the second linked list
* @description: By traversing two linked lists, we can find the intersection node of two one-way linked lists
* @return: com.wp.algorithm.common.SingleNode Return intersecting nodes
* @date: 2021/3/25 1:28 afternoon
* @auther: Mr_wenpan@163.com
*/
public static SingleNode findFistIntersectNode02(final SingleNode head1, final SingleNode head2) {
if (head1 == null || head2 == null) {
return null;
}
SingleNode current1 = head1;
SingleNode current2 = head2;
int listOneLength = 0;
int listTwoLength = 0;
// Count the length of linked list 1, and current1 stops at the last node
while (current1.next != null) {
listOneLength++;
current1 = current1.next;
}
// Count the length of linked list 2, and current2 stops at the last node
while (current2.next != null) {
listTwoLength++;
current2 = current2.next;
}
// If they intersect, the last node of the two linked lists must be the same. If not, they do not intersect.
if (current1 != current2) {
return null;
}
// Find the length difference between the two linked lists
int d = listOneLength - listTwoLength;
// Define long and short list pointers, pointing to long list and short list headers respectively
SingleNode longList;
SingleNode shortList;
// If d > 0, it means that the first linked list is a long linked list, whereas the second linked list is a long linked list
if (d > 0) {
longList = head1;
shortList = head2;
} else {
longList = head2;
shortList = head1;
}
d = Math.abs(d);
// Long linked list first step
for (int i = 0; i < d; i++) {
longList = longList.next;
}
// Long and short linked lists go together until they exit the cycle when they meet
while (longList != shortList) {
longList = longList.next;
shortList = shortList.next;
}
// Return the node that meets
return longList;
}
Case 2: two linked lists have a common ring (the two linked lists have the same ring entry nodes)
In the first case, two single linked lists have no ring structure, and the meeting node is the intersection node.
In this case, because the two linked lists have links, the specific length of each linked list cannot be counted, but the method of calculating the length of the linked list can still be used.
There are two solutions:
The first is to use hash table
The second is to first find the entry node of the two linked list rings, and then calculate the length difference between the two linked lists from the head node to the entry node. Let the long linked list take the difference step first, and then the two linked list pointers go together until they meet. The node they meet is the node where they intersect.
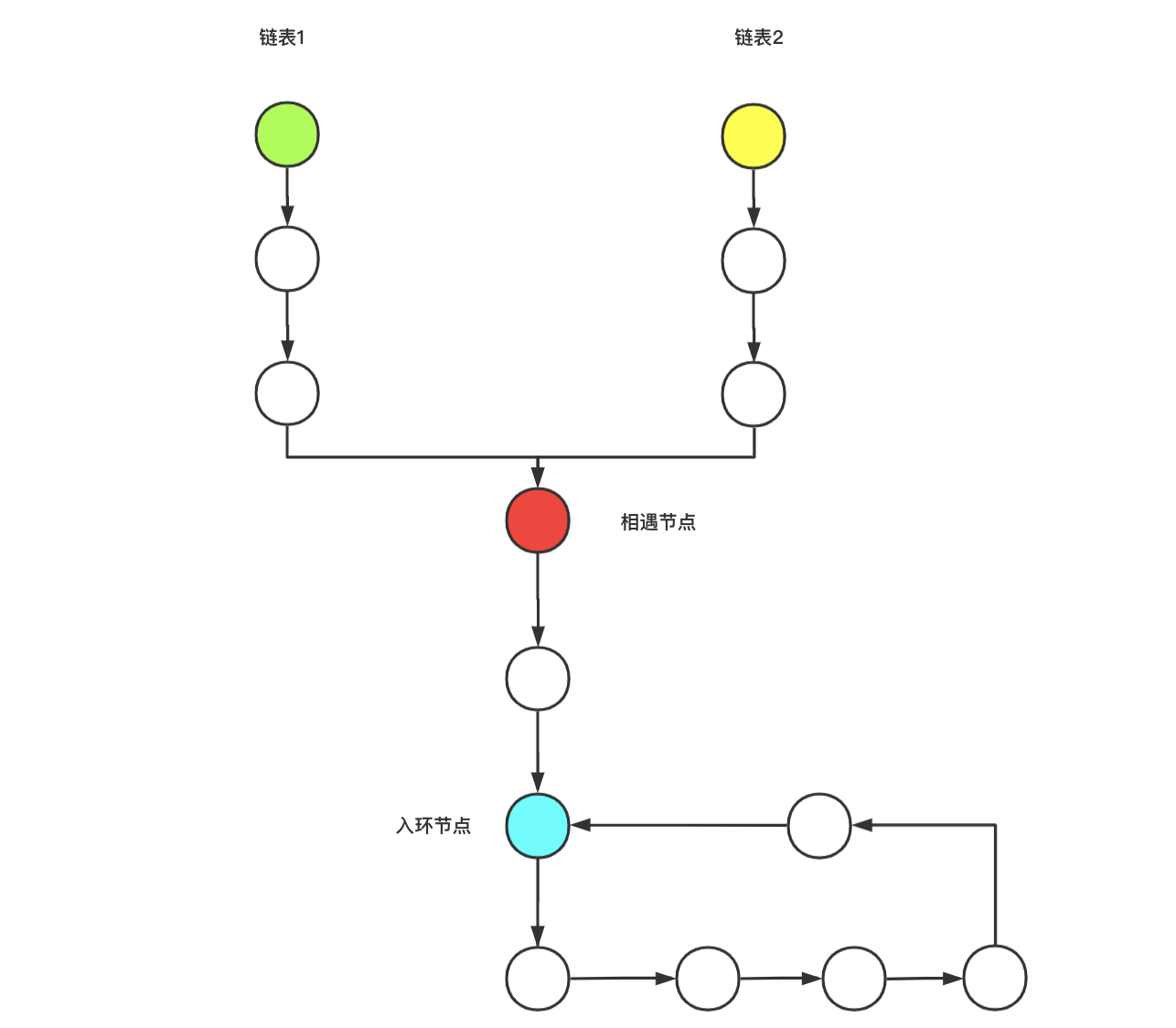
Method 1: use hash table to realize
- Two linked lists are traversed at the same time, and the nodes of the two linked lists are put into the hash table at the same time. For each node, check whether there are the same nodes in the hash table
- If there is, you can directly end the traversal and return to the node.
The code is as follows:
/**
* @param head1 The head node of the first linked list
* @param head2 The head node of the second linked list
* @description: Find the intersection node of two one-way linked lists by hash table + traversing two linked lists (the ring structure of the two intersecting linked lists is applicable)
* @return: com.wp.algorithm.common.SingleNode Return intersecting nodes
* @auther: Mr_wenpan@163.com
*/
public static SingleNode findFistIntersectNode03(final SingleNode head1, final SingleNode head2) {
if (head1 == null || head1 == null) {
return null;
}
final HashSet<SingleNode> hashSet = new HashSet<>();
SingleNode current1 = head1;
SingleNode current2 = head2;
while (current1 != null && current2 != null) {
// First judge whether it exists in the hash table. If it does not exist, add it. If it does exist, the node is the node where the two linked lists intersect
if (hashSet.contains(current1)) {
return current1;
}
hashSet.add(current1);
if (hashSet.contains(current2)) {
return current2;
}
hashSet.add(current2);
current1 = current1.next;
current2 = current2.next;
}
return null;
}
Method 2: find the intersection node of the linked list through the length of the linked list
- First, find the ring on the two linked lists and the entry node of the ring (you can use hash table or speed pointer).
- Then traverse the two linked lists from the head of the two linked lists to the entry node of the ring, and count the length n1 and n2 of this distance.
- Then find the length difference between the two linked lists d = n1 - n2
- The long list goes first
- Then the two linked lists go at the same time until the two linked lists meet. The node they meet is the node they intersect.
The code implementation is as follows:
/**
* Case 2: there is a ring at the intersection, and the nodes entering the ring are different from the intersection nodes, but the nodes entering the ring are the same
* Do this by traversing two linked lists
*/
public static SingleNode findFistIntersectNode04(final SingleNode head1, final SingleNode head2) {
SingleNode cur1 = head1;
SingleNode cur2 = head2;
// The length of the two linked lists from the beginning node to the ring node of the two linked lists
int length1 = 0;
int length2 = 0;
// 1. Find the loop entry node first
final SingleNode cycleNode1 = findInCycleNode(cur1);
final SingleNode cycleNode2 = findInCycleNode(cur2);
// Two linked lists do not intersect
if (cycleNode1 != cycleNode2
|| cycleNode1 == null
|| cycleNode2 == null) {
return null;
}
// 2. Calculate the length from the head node to the ring node of the two linked lists
while (cur1 != cycleNode1) {
cur1 = cur1.next;
length1++;
}
while (cur2 != cycleNode1) {
cur2 = cur2.next;
length2++;
}
// 3. Find out the long linked list and calculate the length difference between the head node and the ring node of the two linked lists
SingleNode longList = length1 > length2 ? head1 : head2;
SingleNode shortList = longList == head1 ? head2 : head1;
final int diff = Math.abs(length1 - length2);
// 4. Long linked list first step
for (int i = 0; i < diff; i++) {
longList = longList.next;
}
// 5. Long and short linked lists go together until they meet. Returning to the meeting node is the intersection node of the two linked lists
while (longList != shortList) {
longList = longList.next;
shortList = shortList.next;
}
// Returns the intersection node of two linked lists
return longList;
}
/**
* Find the entry node of a linked list
*/
public static SingleNode findInCycleNode(final SingleNode head) {
if (head == null) {
return null;
}
SingleNode fast = head;
SingleNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
// The slow pointer catches up with the fast pointer
if (fast == slow) {
break;
}
}
// Two linked lists do not intersect
if (fast == null || fast.next == null) {
return null;
}
// Come on, let's start from the beginning
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
// Return intersection node
return fast;
}
Case 3: two linked lists have a common ring (the ring entry nodes of the two linked lists are different)
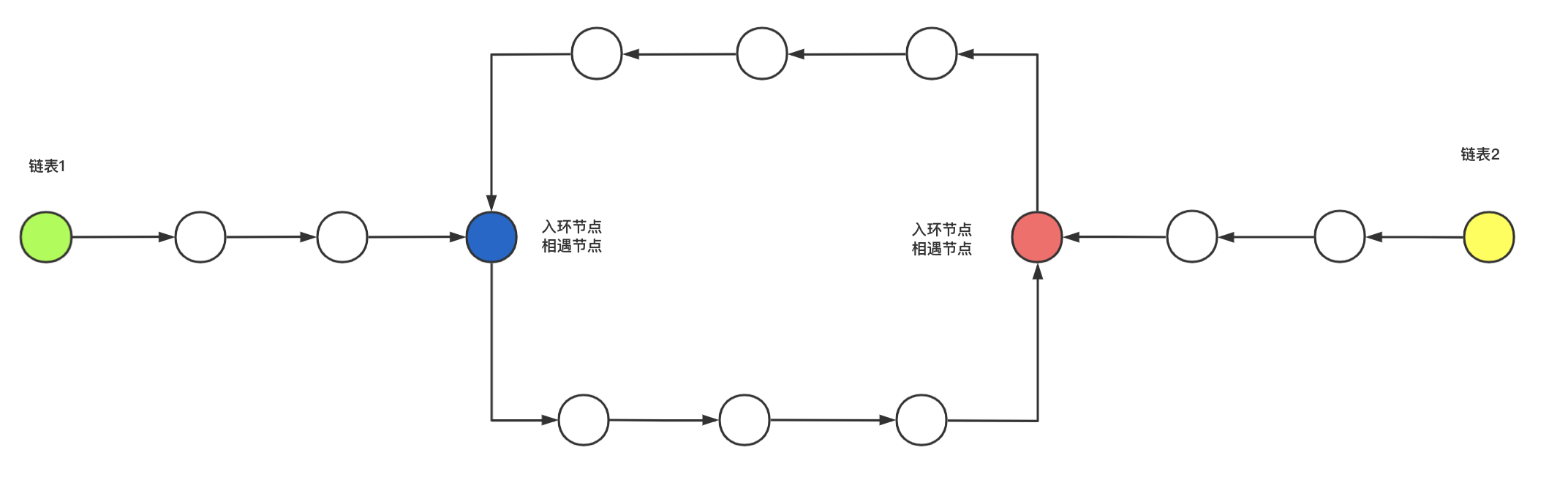
This intersection is special: it has two intersection points, and the entry nodes are different. These two ring nodes are the intersection nodes of the linked list, and only any one can be returned.
The search steps are as follows:
- Find the entry nodes of the two linked lists respectively, and the two pointers stay at the two entry nodes respectively.
- The first pointer stays at the entry node of the first linked list
- The second pointer starts from the entry node of the second linked list and goes down one circle step by step.
- If the second pointer can encounter the first entry node in the process of traversing his ring, it can return this node (this node is the node where the two linked lists intersect)
- If the second pointer has traversed the ring for a week, it still does not encounter the ring entry node of the first linked list. Then you can directly return null (indicating that the two linked lists do not intersect).
The code is as follows:
public static SingleNode findFistIntersectNode05(final SingleNode head1, final SingleNode head2) {
// 1. First find the loop entry nodes of the two linked lists
final SingleNode cycleNode1 = findInCycleNode(head1);
final SingleNode cycleNode2 = findInCycleNode(head2);
// Define two pointers to two nodes respectively
SingleNode cur1;
final SingleNode cur2 = cycleNode2;
// Different loop nodes
if (cycleNode1 != cycleNode2) {
// The first pointer stops at the first ring entry node and the second pointer starts to circle around the second ring entry node to see if it can meet the first ring entry node
cur1 = cycleNode2.next;
while (cur1 != cycleNode2) {
// If cur2 encounters cur1 when traversing the ring, it will directly return cur1. Cur1 or cur2 is the node where they intersect
if (cur1 == cur2) {
return cur1;
}
cur1 = cur1.next;
}
}
return null;
}
2, Integration case 2 and case 3 (with ring)
The above has analyzed and implemented the three situations of linked list intersection one by one. At this time, we should integrate the three situations. Here, first integrate case 2 and case 3. These two cases are intersecting and ring.
The code here is more concise than the code discussed above!!!!
Code example
/**
* @param head1 The head node of the first one-way linked list
* @param loop1 You need to find the first node in the ring
* @param head2 The head node of the second one-way linked list
* @param loop2 The second ring entry node needs to be found by itself and then passed in
* @description: Code demonstration of finding the node where two one-way linked lists meet. This method can deal with the situation that two linked lists intersect and have rings
* @return: com.wp.algorithm.common.SingleNode Return the node that meets
* @auther: Mr_wenpan@163.com
*/
public static SingleNode bothLoop(final SingleNode head1, final SingleNode loop1, final SingleNode head2, final SingleNode loop2) {
SingleNode cur1;
SingleNode cur2;
// 1, The entry node of two linked lists is the same
if (loop1 == loop2) {
cur1 = head1;
cur2 = head2;
int n = 0;
// Calculate the length difference n of the two linked lists (the length difference n from the chain header node to the incoming node)
while (cur1 != loop1) {
n++;
cur1 = cur1.next;
}
while (cur2 != loop2) {
n--;
cur2 = cur2.next;
}
// If n > 0, the linked list of head1 is longer than that of head2
// The function here is to make cur1 point to the long list and cur2 point to the short list
cur1 = n > 0 ? head1 : head2;
cur2 = cur1 == head1 ? head2 : head1;
n = Math.abs(n);
// Let the long linked list go first
while (n != 0) {
n--;
cur1 = cur1.next;
}
// The two linked lists start walking at the same time until the two linked lists meet
while (cur1 != cur2) {
cur1 = cur1.next;
cur2 = cur2.next;
}
// Return encounter node
return cur1;
} else {
// 2, If the ring nodes of two linked lists are not the same
cur1 = loop1.next;
// cur1 takes a circle from the first entry node
while (cur1 != loop1) {
// If you can meet the second node in the ring, you will return. If you can't meet it all the time, it indicates that it doesn't exist and returns null directly
if (cur1 == loop2) {
return loop1;
}
cur1 = cur1.next;
}
// If not found, null is returned
return null;
}
}
3, Integrate all situations
Make a unified integration of the three situations and integrate them into one method.
Code example
public static SingleNode findCommonNode(final SingleNode head1, final SingleNode head2) {
// 1. First find the loop entry nodes of the two linked lists
final SingleNode cycleNode1 = findInCycleNode(head1);
final SingleNode cycleNode2 = findInCycleNode(head2);
final boolean flag = (cycleNode1 == null && cycleNode2 != null) || (cycleNode2 == null && cycleNode1 != null);
// When two linked lists do not intersect, one has a ring and the other has no ring
if (flag) {
return null;
}
// 1, Without ring
if (cycleNode1 == null) {
return findFistIntersectNode02(head1, head2);
} else {
// 2, Case with ring
return bothLoop(head1, cycleNode1, head2, cycleNode2);
}
}
4, Testing
public static void main(final String[] args) {
// Create the first linked list
final SingleNode<String> node1 = new SingleNode<>("1");
final SingleNode<String> node2 = new SingleNode<>("2");
final SingleNode<String> node3 = new SingleNode<>("3");
final SingleNode<String> node4 = new SingleNode<>("4");
final SingleNode<String> node5 = new SingleNode<>("5");
final SingleNode<String> node6 = new SingleNode<>("6");
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
node5.next = node6;
node6.next = node3;
// Create a second linked list
final SingleNode<String> node11 = new SingleNode<>("11");
final SingleNode<String> node12 = new SingleNode<>("12");
final SingleNode<String> node13 = new SingleNode<>("13");
final SingleNode<String> node14 = new SingleNode<>("14");
final SingleNode<String> node15 = new SingleNode<>("15");
final SingleNode<String> node16 = new SingleNode<>("16");
node11.next = node12;
node12.next = node13;
node13.next = node14;
node14.next = node15;
node15.next = node3;
final SingleNode commonNode = findCommonNode(node1, node11);
System.out.println(commonNode);
}