7.1 simple enumeration
In fact, when simple enumeration can pass, don't think of the situation as so complex.
1.Example 7-1 division (UVA 725)
#include<cstdio>
#include<set>
using namespace std;
set<int> cnt;
int N;
int flag;
void solve()
{
int m = 98765 / N, j;
for(int i = 1234; i <= m; i++){
cnt.clear();
j = i * N;
int k = i;
if(j < 10000)
continue;
if(k < 9999)
cnt.insert(0);
while(k > 0){
cnt.insert(k % 10);
k /= 10;
}
while(j > 0){
cnt.insert(j % 10);
j /= 10;
}
if(cnt.size() == 10){
flag = 0;
printf("%05d / %05d = %d\n", i * N, i, N);
}
}
}
int main()
{
int k = 0;
while(scanf("%d", &N) == 1 && N){
if(k++){
printf("\n");
}
flag = 1;
solve();
if(flag)
printf("There are no solutions for %d.\n", N);
}
}
(1) Be careful! Initialization cannot be forgotten! The position of initialization statement cannot be wrong!!!
(2) This question is very strict on the output! There is a blank line between each example, but there is no blank line after the last example.
(3) There is also a pit in this question. Look at the output! 0 should be filled in front of the four digits. Use the form "% 05d" to occupy 5 digits. If the length is not enough, use 0 to fill in.
2.Example 7-2 maximum product (UVA 11059)
Such a simple question, direct violent search is not enough. Why do you have to deal with those fancy ones. I will not delete the last two solutions as a warning and a long lesson.
FA Yi (too violent, too violent):
#include<cstdio>
#include<algorithm>
using namespace std;
int N, a[20];
typedef long long ll;
int main()
{
int kase = 0;
ll res = 0;
while(scanf("%d", &N) == 1){
res = 0;
for(int i = 0; i < N; i++){
scanf("%d", &a[i]);
}
for(int i = 0; i < N; i++){
ll tmp = 1;
for(int j = i; j < N; j++){
tmp *= a[j];
res = max(res, tmp);
}
}
printf("Case #%d: The maximum product is %lld.\n\n", ++kase, res);
}
return 0;
}Act II (more violent and WA):
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
int a[23], N, kase, tmp[23];
typedef long long ll;
ll res = 0;
ll mul(int sz)
{
ll res1 = 1;
int neg[20], x = 0; //Store the subscripts of negative numbers and the number of negative numbers.
for(int i = 0; i < sz; i++){
if(tmp[i] < 0)
neg[x++] = i;
res1 *= (ll)tmp[i];
}
// printf("%lld, %d\n", res1, x);
if(res1 > 0)
return res1;
else if(sz == 1 && x == 1)
return res1;
else{
ll res2 = res1;
for(int i = 0; i <= neg[0]; i++)
res2 /= (ll)tmp[i];
for(int i = neg[x - 1]; i < sz; i++)
res1 /= (ll)tmp[i];
return max(res1, res2);
}
}
int main()
{
while(scanf("%d", &N) == 1){
vector<int> Z[23]; //It is equivalent to initializing vector here every time
res = 0;
int idx = 0, flag = 0;
for(int i = 0; i < N; i++){
scanf("%d", &a[i]);
}
for(int i = 0; i < N; i++){
if(a[i] != 0){ //Divide the array by 0.
flag = 0;
Z[idx].push_back(a[i]);
}
else{ // Prevent the occurrence of two zeros and zero at the beginning
idx++;
}
}
for(int i = 0; i < idx; i++){
for(int j = 0; j < Z[i].size(); j++){
tmp[j] = Z[i][j];
}
if(Z[i].size() != 0)
res = max(res, mul(Z[i].size()));
}
printf("Case #%d: The maximum product is %lld.\n\n", ++kase, res);
}
return 0;
}
Method 3 (WA):
Generally speaking, the ruler method is to reduce the complexity. Therefore, the interval should not be too long, especially covering almost the whole array. Therefore, the ruler method is not appropriate for this problem.
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
int a[23], N, kase, tmp[23];
typedef long long ll;
ll res = 0;
ll mul(int sz)
{
ll res0[20] = {tmp[0]}, res1 = tmp[0]; //In case the first number is the answer.
for(int i = 1; i < sz; i++){
res1 = max(res1, (ll)tmp[i]);
res0[i] = res0[i - 1] * tmp[i];
res1 = max(res1, res0[i]); //Here is to multiply all subscripts from zero.
}
for(int i = 1; i < sz; i++){
for(int j = 0; j < i; j++){
res1 = max(res1, res0[i] / res0[j]); //The trailing mark starts from 0, and the trailing mark does not exceed the leading mark.
}
}
return res1;
}
int main()
{
while(scanf("%d", &N) == 1){
vector<int> Z[23]; //It is equivalent to initializing vector here every time
res = 0;
int idx = 0, flag = 0;
for(int i = 0; i < N; i++){
scanf("%d", &a[i]);
}
for(int i = 0; i < N; i++){
if(a[i] != 0){ //Divide the array by 0.
flag = 0;
Z[idx].push_back(a[i]);
}
else{ // Prevent the occurrence of two zeros and zero at the beginning
if(flag)
continue;
else{
idx++;
flag = 1;
}
}
}
for(int i = 0; i <= idx; i++){
for(int j = 0; j < Z[i].size(); j++){
tmp[j] = Z[i][j];
}
res = max(res, mul(Z[i].size()));
}
printf("Case #%d: The maximum product is %lld.\n\n", ++kase, res);
}
return 0;
}
(1) Three methods were used.
(2) Note that when there is 0 in the middle, 0 is not the part of the required continuous subsequence. Take 0 as the dividing point to divide the array into several parts.
(3) Again, we must pay attention to the output format. No matter what website it is, there must be a carriage return after the output result!
(4) See the output format. Is there a blank line between each example or after each example.
3.Example 7-3 Fractions Again?!, UVa 10976
//The min() function is defined in < algorithm > and < vector >. In addition, we should say less in the future.
#include<cstdio>
#include<algorithm>
using namespace std;
int k;
int N;
int X[10000], Y[10000];
void solve()
{
N = 0;
int y = k, x = k + 1, m; //Give x a random initial value, mainly because X and y cannot be equal.
while(x != y){ //Because a fraction can always be written as the sum of the other two fractions, that is, the denominator is twice K. Therefore, the limiting condition can also be written as y < = 2 * k;
y++;
m = k * y / (y - k);
if(m * (y - k) != k * y){
// printf("I'm here\n");
continue;
}
x = m;
X[N] = x;
Y[N++] = y;
}
printf("%d\n", N);
for(int i = 0; i < N; i++){
printf("1/%d = 1/%d + 1/%d\n", k, X[i], Y[i]);
}
}
int main()
{
while(scanf("%d", &k) == 1){
solve();
}
return 0;
}
(1) There's nothing to say, water problem. Pay attention to two points: one is how to judge whether to divide or not, which can be done through simple transformation; the other is to pay attention to the termination condition, which stops when x = y = 2k, and Y is gradually increasing and X is gradually decreasing. In this way, the termination condition can be written in several forms.
7.2 enumeration arrangement
1. Generate arrangement of 1~n
Note: This is only an arrangement of 1~n, not an arbitrary arrangement.
#include<cstdio>
int A[100], P[100];
void print_permutation(int n, int cur)
{
if(cur == n){
for(int i = 0; i < n; i++){
printf("%d ", A[i]);
}
printf("\n");
}
else for(int i = 1; i <= n; i++){
int ok = 1;
for(int j = 0; j < cur; j++){
if(A[j] == i) ok = 0;
}
if(ok){
A[cur] = i;
print_permutation(n, cur + 1);
}
}
}
int main()
{
print_permutation(4, 0);
return 0;
}
2. Generate repeatable permutations
#include<cstdio>
int A[100], P[100];
void print_permutation(int n, int cur)
{
if(cur == n){
for(int i = 0; i < n; i++){
printf("%d ", A[i]);
}
printf("\n");
}
else for(int i = 0; i < n; i++)
if(!i || P[i] != P[i - 1]){
int c1 = 0, c2 = 0;
for(int j = 0; j < cur; j++) if(A[j] == P[i]) c1++;
for(int j = 0; j < n; j++) if(P[j] == P[i]) c2++;
if(c1 < c2){
A[cur] = P[i];
/*
At first cur=0, there must be C1 < C2, which is equivalent to putting each element in the first position of A, and so on.
Then, after arranging P, only the unequal elements in P are passed in.
*/
print_permutation(n, cur + 1);
}
}
}
int main()
{
P[0] = 1, P[1] = 1, P[2] = 1, P[3] = 8;
print_permutation(4, 0);
return 0;
}
3. Answer tree
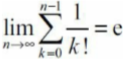
Through computer simulation, it is found that it converges quickly (n = 15 doesn't change much)
7.3 subset generation
Incremental construction method
Note: This is only a subset of the set whose enumeration element is 0~n-1.
#include<cstdio>
int A[100];
void print_subset(int n, int cur)
{
for(int i = 0; i < cur; i++){
printf("%d ", A[i]);
}
if(cur)
printf("\n");
int s = cur ? A[cur - 1] + 1 : 0;
for(int i = s; i < n; i++){
A[cur] = i;
print_subset(n, cur + 1);
}
}
int main()
{
print_subset(4, 0);
return 0;
}
Bit vector method
This can generate A subset of any set. In the following code, the set is A and the bit vector is B;
#include<cstdio>
int A[100] = {2,5,8,4,3}, B[100];
void print_subset(int n, int cur)
{
if(cur == n){
for(int i = 0; i < n; i++){
if(B[i])
printf("%d ", A[i]);
}
printf("\n");
}
else{
B[cur] = 1;
print_subset(n, cur + 1);
B[cur] = 0;
print_subset(n, cur + 1);
}
}
int main()
{
print_subset(4, 0);
return 0;
}
Binary method (simplest)
(1) Complete set: ALL_BITS: (1 < < n) - 1
(2) Complement of A: ALL_BITS ^ A (bitwise XOR is fast)
(3) Print subset
#include<cstdio>
using namespace std;
void print_subset(int n, int s)
{
for(int i = 0; i < n; i++){
if(s >> i & 1)
printf("%d ", i);
printf("\n");
}
}
(4) enumeration subset
for(int i = 0; i < (1 << n); i++)
print_subset(n, i);7.4 backtracking method
1. Question of Queen VIII
(1) At the beginning, I also thought that the queens were in different rows and different columns. However, at the beginning, I thought that it was troublesome to use the set to duplicate. It was convenient to use the full arrangement. However, if each row and column had a full arrangement, it would be (8!)^ 2. High complexity.
(2) However, in fact, it only needs to be fully arranged once, and each row is placed in order, and each column is fully arranged with recursive functions. If the conditions are not met, it will be traced back. In fact, the complexity is O(n!), And a lot of calculations can be reduced by backtracking.
(3) The second condition can be regarded as the absolute value of the slope of the two-point connecting line. Once it is 1, it break s;
(4) This question is very classic. You must memorize it.
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int X[100], Y[100], tot, N;
void search(int cur)
{
if(cur == N){ //Notice that it's N, not N - 1. Think about why.
tot++;
}
else for(int i = 0; i < N; i++){
int ok = 1;
Y[cur] = i; //The elements in row cur are placed in column i. cur is increased from 0 to N, not all arranged.
for(int j = 0; j < cur; j++){
if(Y[j] == Y[cur] || abs(cur - j) == abs(Y[cur] - Y[j])){
ok = 0;
break;
}
}
if(ok)
search(cur + 1);
}
}
int main()
{
scanf("%d", &N);
for(int i = 0; i < N; i++){
X[i] = i;
}
search(0);
printf("%d\n", tot);
return 0;
}
(this method is not easy to understand, mainly learning from the above method) of course, there is a method with lower complexity, that is, marking the main diagonal with x + y and marking the sub diagonal with y - x. however, since y - x may be negative, add n, so that all y - x are added with N, and effectively check whether it is repeated. As long as the array is large enough, it can ensure that the array will not cross the boundary.
#include<cstdio>
int N, tot, vis[3][200], C[100];
void search(int cur)
{
if(cur == N)
tot++;
else for(int i = 0; i < N; i++)
if(!vis[0][i] && !vis[1][cur + i] && !vis[2][i - cur + N]){
C[cur] = i; //If the solution is not printed, it can be ignored.
vis[0][i] = vis[1][cur + i] = vis[2][i - cur + N] = 1;
search(cur + 1);
vis[0][i] = vis[1][cur + i] = vis[2][i - cur + N] = 0;
}
}
int main()
{
scanf("%d", &N);
search(0);
printf("%d\n", tot);
return 0;
}
I have studied data structure in my freshman year, which is also an achievement, and there is a great difference between data structure and competition. I won't learn it first. Concentrate all your energy (basic course, English is to learn).
2.Example 7-4 prime ring problem (UVA 524)
(1) Let's take a look at Mr. Liu Rujia's method first (there seems to be a pit in the output):
(2) In fact, it should be faster. After all, has this been used? i uses an array instead of traversal search. In fact, this method is also more concise. By the way, it also uses a prime sieve.
(3) Chen Feng said that sometimes using STL will be slow, but the code readability will be greatly improved, and it will be relatively easy to design. Therefore, it is actually very convenient to use STL without timeout.
#include<cstdio>
#include<cstring>
bool is_prime[55], visit[55];
int A[20];
int N, kase;
void sieve(int n)
{
int p = 0;
memset(is_prime, true, sizeof(is_prime));
is_prime[0] = is_prime[1] = false;
for(int i = 2; i <= n; i++){
if(is_prime[i]){
for(int j = 2 * i; j <= n; j += i){
is_prime[j] = false;
}
}
}
}
void dfs(int cur)
{
if(cur == N && is_prime[A[0] + A[N - 1]]){
for(int i = 0; i < N; i++){
printf("%d%c", A[i], i + 1 == N ? '\n' : ' ');
}
}
else for(int i = 2; i <= N; i++){
if(!visit[i] && is_prime[i + A[cur - 1]]){
A[cur] = i;
visit[i] = true;
dfs(cur + 1);
visit[i] = false;
}
}
}
int main()
{
sieve(50);
A[0] = 1;
while(scanf("%d", &N) == 1){
if(kase) printf("\n");
printf("Case %d:\n", ++kase);
memset(visit, false, sizeof(visit));
visit[1] = true;
dfs(1);
}
return 0;
}
(2) this method is a little slow, 300MS.
#include<cstdio>
#include<cstring>
using namespace std;
int N, A[100] = {1}, kase = 0;
bool isPrime(int n)
{
if(n == 2)
return true;
else if(n % 2 == 0)
return false;
else
for(int i = 3; i * i <= n; i += 2){
if(n % i == 0)
return false;
}
return true;
}
void loop_search(int cur)
{
if(cur == N){
if(isPrime(A[N - 1] + A[0])){
for(int i = 0; i < N - 1; i++)
printf("%d ", A[i]);
printf("%d\n", A[N - 1]);
}
}
else for(int i = 2; i <= N; i++){
int ok = 1;
if(!isPrime(A[cur - 1] + i)){
ok = 0;
}
for(int j = 0; j < cur; j++){
if(A[j] == i){
ok = 0;
break;
}
}
A[cur] = i;
if(ok)
loop_search(cur + 1);
}
}
int main()
{
while(scanf("%d", &N) == 1){
memset(A, 0, sizeof(A));
A[0] = 1;
if(kase){
printf("\n");
}
printf("Case %d:\n", ++kase);
loop_search(1);
}
}
3.Example 7-5 difficult string (Krypton Factor, UVa 129)
(1) A few small details have been changed to better understand than the original book. This is a bit similar to but different from the periodic string. Because adding a letter to a difficult string may lead to repeated strings with variable length at the back, we should check them one by one, that is, check the suffix as mentioned in the book. Check whether the last two elements, the last four elements and the last six elements can be used from Split the middle into two repeated strings?
(2) The output of this question still has some skills.
(3) Another difficulty is how to put the first L elements one by one? The answer is backtracking.
#include<cstdio>
#include<algorithm>
using namespace std;
int S[100], cnt, N, L; //See, it's cnt, not cur!!!
int dfs(int cur)
{
if(cnt == N){
for(int i = 0; i < cur; i++){
if(i && i % 64 == 0){
printf("\n");
}
else if(i && i % 4 == 0){
printf(" ");
}
printf("%c", S[i] + 'A');
}
printf("\n%d\n", cur);
return 0;
}
for(int i = 0; i < L; i++){
S[cur] = i;
int ok = 1;
for(int j = 1; j * 2 <= cur + 1; j++){
int equal = 1;
for(int k = 0; k < j; k++){
if(S[cur - k] != S[cur - k - j]){
equal = 0; break;
}
}
if(equal) {ok = 0; break;}
}
if(ok){
cnt++;
if(!dfs(cur + 1)) return 0;
}
}
return 1;
}
int main()
{
while(scanf("%d%d", &N, &L) && N){
cnt = 0;
dfs(0);
}
}
4.Example 7-6 bandwidth (UVA 140)
(1) 8! = 40320, such a small number, there is no need to consider others. However, I added: if (bandwidth > = ANS) break;
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn = 10;
int id[256], letter[maxn];
int main() {
char input[1000];
while (scanf("%s", input) == 1 && input[0] != '#') {
int n = 0;
for(char ch = 'A'; ch <= 'Z'; ch++)
if (strchr(input, ch) != NULL) {
id[ch] = n++;
letter[id[ch]] = ch;
}
int len = strlen(input), p = 0, q = 0;
vector<int> u, v;
while(true) {
while (p < len && input[p] != ':') p++;
if (p == len) break;
while (q < len && input[q] != ';') q++;
for (int i = p + 1; i < q; i++) {
u.push_back(id[input[p - 1]]);
v.push_back(id[input[i]]);
}
p++; q++;
}
int P[maxn], bestP[maxn], pos[maxn], ans = n;
for (int i = 0; i < n; i++) P[i] = i;
do {
for (int i = 0; i < n; i++) pos[P[i]] = i;
int bandwidth = 0;
for (int i = 0; i < u.size(); i++) {
bandwidth = max(bandwidth, abs(pos[u[i]] - pos[v[i]]));
if (bandwidth >= ans) break;
}
if (bandwidth < ans) {
ans = bandwidth;
memcpy(bestP, P, sizeof(P));
}
} while (next_permutation(P, P + n));
for (int i = 0; i < n; i++) printf("%c ", letter[bestP[i]]);
printf("-> %d\n", ans);
}
return 0;
}5.Example 7-7 balance problem (mobile computing, ACM / ICPC, Tokyo 2005, uva1354)
(1) Data structures have to be learned. Every time Liu Rujia talks about trees, I'm not very good at them.
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
struct Tree {
double L, R;
Tree() :L(0), R(0) {}
};
const int maxn = 6;
int n, vis[1 << maxn];
double r, w[maxn], sum[1 << maxn];
vector<Tree> tree[1 << maxn];
void dfs(int subset) {
if (vis[subset]) return;
vis[subset] = true;
bool have_children = false;
//Can you enumerate subtrees like this
for (int left = (subset - 1) & subset; left; left = (left - 1) & subset) {
have_children = true;
int right = subset ^ left;
double d1 = sum[right] / sum[subset];
double d2 = sum[left] / sum[subset];
dfs(left); dfs(right);
for (int i = 0; i < tree[left].size(); i++) {
for (int j = 0; j < tree[right].size(); j++) {
Tree t;
//The handling of this step is still very rigorous
t.L = max(tree[left][i].L + d1, tree[right][j].L - d2);
t.R = max(tree[right][j].R + d2, tree[left][i].R - d1);
if (t.L + t.R < r) tree[subset].push_back(t);
}
}
}
//This step is very necessary. Without this step, we can't enter the above double cycle.
if (!have_children) tree[subset].push_back(Tree());
}
int main() {
int T;
scanf("%d", &T);
while (T--) {
scanf("%lf%d", &r, &n);
for (int i = 0; i < n; i++) scanf("%lf", &w[i]);
for (int i = 0; i < (1 << n); i++) {
sum[i] = 0;
tree[i].clear();
for (int j = 0; j < n; j++)
if (i & (1 << j)) sum[i] += w[j];
}
int root = (1 << n) - 1;
memset(vis, 0, sizeof(vis));
dfs(root);
double ans = -1;
for (int i = 0; i < tree[root].size(); i++) {
ans = max(ans, tree[root][i].L + tree[root][i].R);
}
printf("%.10f\n", ans);
}
return 0;
}7.5 path finding problem
(VIII) digital issues
(1) The textbook simulates the queue without using STL. Finally, I didn't understand the coding problem. I learned only one of the three methods. It is said that it will be taught in Chapter 10. Sure enough, I should learn new knowledge in the morning and write exercises in the afternoon, otherwise I will always have something I haven't learned.
#include<cstdio>
#include<cstring>
using namespace std;
typedef int State[9];
const int maxstate = 1e6;
State st[maxstate], goal;
int dist[maxstate];
int vis[362880], fact[9];
const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1};
void init_lookup_table()
{
fact[0] = 1;
for(int i = 1; i < 9; i++) fact[i] = fact[i - 1] * i; // factorial
}
int try_to_insert(int s)
{
int code = 0;
for(int i = 0; i < 9; i++){
int cnt = 0;
for(int j = i + 1; j < 9; j++) if(st[s][j] < st[s][i]) cnt++;
code += fact[8 - i] * cnt;
}
if(vis[code]) return 0;
return vis[code] = 1;
}
int bfs()
{
init_lookup_table();
int front = 1, rear = 2;
while(front < rear){
State& s = st[front];
if(memcmp(goal, s, sizeof(s)) == 0) return front;
int z;
for(z = 0; z < 9; z++) if(!s[z]) break;
int x = z / 3, y = z % 3;
for(int d = 0; d < 4; d++){
int newx = x + dx[d];
int newy = y + dy[d];
int newz = newx * 3 + newy;
if(newx >= 0 && newx < 3 && newy >= 0 && newy < 3){
State& t = st[rear];
memcpy(&t, &s, sizeof(s));
t[newz] = s[z];
t[z] = s[newz];
dist[rear] = dist[front] + 1;
if(try_to_insert(rear)) rear++;
}
}
front++;
}
return 0;
}
int main()
{
for(int i = 0; i < 9; i++) scanf("%d", &st[1][i]);
for(int i = 0; i < 9; i++) scanf("%d", &goal[i]);
int ans = bfs();
if(ans > 0) printf("%d\n", dist[ans]);
else printf("-1\n");
return 0;
}
2.Example 7-8 water pouring problem (Fill, UVa 10603)
(1) Liu Rujia said that there is also Dijkstra algorithm, which can be obtained with a little modification. In fact, I am not very good at establishing this figure.
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
struct Node
{
int v[3], dist;
bool operator < (const Node& rhs) const
{
return dist > rhs.dist;
}
};
const int maxn = 200 + 5;
int vis[maxn][maxn], cap[3], ans[maxn];
void update_ans(const Node& u)
{
for(int i = 0; i < 3; i++){
int d = u.v[i];
if(ans[d] < 0 || u.dist < ans[d]) ans[d] = u.dist;
}
}
void solve(int a, int b, int c, int d)
{
cap[0] = a; cap[1] = b; cap[2] = c; //Capacity container capacity.
memset(vis, 0, sizeof(vis));
memset(ans, -1, sizeof(ans));
priority_queue<Node> q;
Node start;
start.dist = 0;
start.v[0] = 0, start.v[1] = 0; start.v[2] = c;
q.push(start);
vis[0][0] = 1;
while(!q.empty()){
Node u = q.top(); q.pop();
update_ans(u);
if(ans[d] >= 0) break;
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++) if(i != j){
if(u.v[i] == 0 || u.v[j] == cap[j]) continue;
int amount = min(cap[j], u.v[i] + u.v[j]) - u.v[j]; //Pour i into j.
Node u2;
memcpy(&u2, &u, sizeof(u));
u2.dist = u.dist + amount;
u2.v[i] -= amount;
u2.v[j] += amount;
if(!vis[u2.v[0]][u2.v[1]]){
vis[u2.v[0]][u2.v[1]] = 1;
q.push(u2);
}
}
}
}
while(d >= 0){
if(ans[d] >= 0){
printf("%d %d\n", ans[d], d);
return;
}
d--;
}
}
int main()
{
int T, a, b, c, d;
scanf("%d", &T);
while(T--){
scanf("%d%d%d%d", &a, &b, &c, &d);
solve(a, b, c, d);
}
return 0;
}
3.Example 7-9 The Morning after Halloween, Japan 2007, UVa1601
7.6 iterative deepening search
1. Egypt scores
(1) For problems that can be solved by backtracking method but have no obvious upper limit on the depth of the solution tree, iterative deepening search can be considered. If an optimistic evaluation function can be designed to predict that the solution can be obtained only by expanding at least several layers of nodes from the current node, iterative deepening search becomes IDA * algorithm.