preface
If you think the article is helpful, please leave some praise and collection. Pay attention to xiaoleng and read more dry goods learning articles
★ this is Xiao Leng's blog ‡ see the column for good articles on high-quality technology The official account of the individual, sharing some technical articles, and the pit encountered. Current series: data structure series Source code git warehouse Data structure code address Code Git warehouse address
catalogue
Cued binary tree
The cue binary tree is introduced through a problem
The sequence {1,3,6,8,10,14} is constructed into a binary tree n+1=7
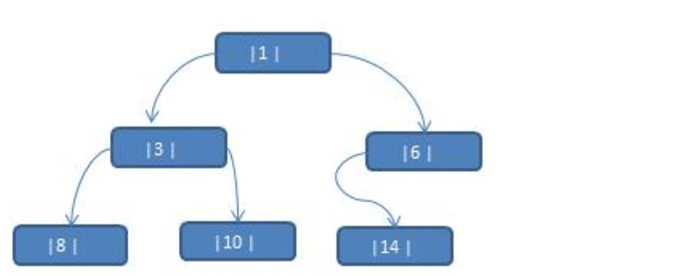
Problem analysis:
- When we traverse the above binary tree in middle order, the sequence is {8, 3, 10, 1, 6, 14}
- However, the left and right pointers of nodes 6, 8, 10 and 14 are not fully utilized
- What if we want to make full use of the left and right pointers of each node so that each node can point to its own front and rear nodes?
- Solution - clue binary tree
Basic introduction of clue binary tree
- The binary linked list of N nodes contains n+1 [Formula 2n-(n-1)=n+1] empty finger needle fields. The null pointer field in the binary linked list is used to store pointers to the precursor and successor nodes of the node in a certain traversal order (this additional pointer is called "clue")
- This binary linked list with clues is called clue linked list, and the corresponding binary tree is called threaded binary tree. According to the different properties of clues, clue binary trees can be divided into three types: pre order clue binary trees, middle order clue binary trees and post order clue binary trees
- The previous node of a node is called the precursor node
- The next node of a node is called the successor node
Application case of clue binary tree
Put the following binary tree into the middle order clue binary tree. The number sequence traversed in the middle order is {8, 3, 10, 1, 14, 6}

Note: after cueing the binary tree, the attributes left and right of the Node are as follows:
- Left refers to the left subtree or the precursor node For example, ① node left points to the left subtree, while ⑩ node left points to the left subtree Is the precursor node
- Right refers to the right subtree or the successor node. For example, ① node right refers to the right subtree, while ⑩ node right refers to the successor node
code implementation
package com.hyc.DataStructure.tree.ThreadedBinaryTree;
/**
* @projectName: DataStructure
* @package: com.hyc.DataStructure.tree.ThreadedBinaryTree
* @className: ThreadedBinaryTreeDemo
* @author: Cold Huanyuan doorwatcher
* @description: TODO
* @date: 2022/2/5 16:38
* @version: 1.0
*/
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
//Test the function of a medium order clue binary tree
heroNode root = new heroNode(1, "tom");
heroNode node2 = new heroNode(3, "jack");
heroNode node3 = new heroNode(6, "smith");
heroNode node4 = new heroNode(8, "mary");
heroNode node5 = new heroNode(10, "king");
heroNode node6 = new heroNode(14, "dim");
//The binary tree will be created recursively later. Now it is easy to create it manually
root.setLeftNode(node2);
root.setRightNode(node3);
node2.setLeftNode(node4);
node2.setRightNode(node5);
node3.setLeftNode(node6);
//Sequential cueing in testing
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setHead(root);
threadedBinaryTree.postThreadedNodes(root);
//Test: test with node 10
heroNode leftNode = node5.getLeftNode();
heroNode rightNode = node5.getRightNode();
System.out.println("10 The precursor node of node is =" + leftNode); //3
System.out.println("10 The successor node of node is=" + rightNode); //1
//When the binary tree is threaded, the original traversal method can be used
//threadedBinaryTree.infixOrder();
System.out.println("Traversing the cued binary tree in a cued way");
threadedBinaryTree.preThreaddeList(); // 8, 3, 10, 1, 14, 6
}
}
class ThreadedBinaryTree {
//Determine root node
private heroNode head;
//During recursion, the variables used to store the previous node are used to traverse the cued tree and cued nodes
private heroNode pre;
public void setHead(heroNode head) {
this.head = head;
}
//Cued traversal
public void ThreaddeList() {
// Here we need a variable to store the current node
heroNode tempNode = head;
while (tempNode != null) {
/* Start loop traversal
* Loop to find the node with lefttype 1, so the first one to find is the node with node value of 8
* Later, it will change with traversal. When lefttype ==1 is found, it indicates that the tree has been cued
* After that, you only need to deal with the effective nodes after cueing
* */
while (tempNode.getLefttype() == 0) {
tempNode = tempNode.getLeftNode();
}
// Because it is a medium order traversal, the order is: left, middle and right. Here, we are from the left lefttype==1, that is, it is the first node at the beginning of the left, so we can output it directly
System.out.println(tempNode);
/* If the right pointer of the current node points to the subsequent node, it will be output all the time
* */
while (tempNode.getRighttype() == 1) {
tempNode = tempNode.getRightNode();
System.out.println(tempNode);
}
// Replace this traversal node
tempNode = tempNode.getRightNode();
}
}
public void preThreaddeList() {
// Here we need a variable to store the current node
heroNode tempNode = head;
while (tempNode != null) {
/* Start loop traversal
* Loop to find the node with lefttype 1, so the first one to find is the node with node value of 8
* Later, it will change with traversal. When lefttype ==1 is found, it indicates that the tree has been cued
* After that, you only need to deal with the effective nodes after cueing
* */
while (tempNode.getLefttype() == 0) {
System.out.println(tempNode);
tempNode = tempNode.getLeftNode();
}
// Because it is a medium order traversal, the order is: left, middle and right. Here, we are from the left lefttype==1, that is, it is the first node at the beginning of the left, so we can output it directly
System.out.println(tempNode);
// Traversal of this node
tempNode = tempNode.getRightNode();
}
}
//Cued node
public void ThreadedNodes(heroNode node) {
// Non null judgment
if (node == null) {
return;
}
// Cued left subtree
ThreadedNodes(node.getLeftNode());
// Cued node
//It's not easy to understand. Here's 8 an example
// 8's left ==null, then 8's lefttype = 1 means that it is a precursor node
if (node.getLeftNode() == null) {
//If the left pointer of the current node is null, then point her left pointer to the pre preceding node
//Taking 8 as an example, when the method pre is empty for the first time, so 8 has no front node, it is the front node itself, so the left pointer state is 1
node.setLeftNode(pre);
// After pointing, change the type to 1
node.setLefttype(1);
}
//Processing successor nodes
//The leading node judged here is not empty, and the leading node has no successor node
if (pre != null && pre.getRightNode() == null) {
//Here, take the latter node of 8 as an example. When the pointer points to 3, the front node pre = 8, which means that the rightnode of 8 is 3
pre.setRightNode(node);
//At this time, the post node is not a subtree, and when the right pointer of the pre node points to the node, changing the right state to 1 indicates that it is the successor node
pre.setRighttype(1);
}
//Every time a node is processed, we need to store it in pre, that is, the front node
//Otherwise, it will cause dead recursion
pre = node;
// Cued right subtree
ThreadedNodes(node.getRightNode());
}
//Cued node
public void preThreadedNodes(heroNode node) {
// Non null judgment
if (node == null) {
return;
}
// Cued node
//It's not easy to understand. Here's 8 an example
// 8's left ==null, then 8's lefttype = 1 means that it is a precursor node
if (node.getLeftNode() == null) {
//If the left pointer of the current node is null, then point her left pointer to the pre preceding node
//Taking 8 as an example, when the method pre is empty for the first time, so 8 has no front node, it is the front node itself, so the left pointer state is 1
node.setLeftNode(pre);
// After pointing, change the type to 1
node.setLefttype(1);
}
//Processing successor nodes
//The leading node judged here is not empty, and the leading node has no successor node
if (pre != null && pre.getRightNode() == null) {
//Here, take the latter node of 8 as an example. When the pointer points to 3, the front node pre = 8, which means that the rightnode of 8 is 3
pre.setRightNode(node);
//At this time, the post node is not a subtree, and when the right pointer of the pre node points to the node, changing the right state to 1 indicates that it is the successor node
pre.setRighttype(1);
}
//Every time a node is processed, we need to store it in pre, that is, the front node
//Otherwise, it will cause dead recursion
pre = node;
if (node.getLefttype() == 0) {
// Cued left subtree
preThreadedNodes(node.getLeftNode());
}
if (node.getRighttype() == 0) {
// Cued right subtree
preThreadedNodes(node.getRightNode());
}
}
//Cued node
public void postThreadedNodes(heroNode node) {
// Non null judgment
if (node == null) {
return;
}
// Cued left subtree
ThreadedNodes(node.getLeftNode());
// Cued right subtree
ThreadedNodes(node.getRightNode());
// Cued node
//It's not easy to understand. Here's 8 an example
// 8's left ==null, then 8's lefttype = 1 means that it is a precursor node
if (node.getLeftNode() == null) {
//If the left pointer of the current node is null, then point her left pointer to the pre preceding node
//Taking 8 as an example, when the method pre is empty for the first time, so 8 has no front node, it is the front node itself, so the left pointer state is 1
node.setLeftNode(pre);
// After pointing, change the type to 1
node.setLefttype(1);
}
//Processing successor nodes
//The leading node judged here is not empty, and the leading node has no successor node
if (pre != null && pre.getRightNode() == null) {
//Here, take the latter node of 8 as an example. When the pointer points to 3, the front node pre = 8, which means that the rightnode of 8 is 3
pre.setRightNode(node);
//At this time, the post node is not a subtree, and when the right pointer of the pre node points to the node, changing the right state to 1 indicates that it is the successor node
pre.setRighttype(1);
}
//Every time a node is processed, we need to store it in pre, that is, the front node
//Otherwise, it will cause dead recursion
pre = node;
}
// Preorder traversal
public void preOrder() {
if (this.head != null) {
this.head.PreOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Middle order traversal
public void InfixOrder() {
if (this.head != null) {
this.head.infixOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Subsequent traversal
public void PostOrder() {
if (this.head != null) {
this.head.postOrder();
} else {
System.out.println("Binary tree has no root node and cannot be traversed");
}
}
//Preorder search
public heroNode preOrderSearch(int no) {
if (this.head != null) {
return this.head.PreOrderSearch(no);
} else {
return null;
}
}
//Medium order search
public heroNode infixOrderSearch(int no) {
if (this.head != null) {
return this.head.infixOrderSearch(no);
} else {
return null;
}
}
//Sequential search
public heroNode postOrderSearch(int no) {
if (this.head != null) {
return this.head.postOrderSearch(no);
} else {
return null;
}
}
// Delete node
public void deleteNode(int no) {
if (head != null) {
if (head.getId() == no) {
head = null;
return;
} else {
head.deleteNode(no);
}
} else {
System.out.println("Empty tree,Cannot delete");
}
}
}
class heroNode {
private int id;
private String name;
private heroNode leftNode;
private heroNode rightNode;
//If the type is 0, it means that there is a subtree. If the type is 1, it means that it is a precursor node / post node
private int lefttype;
private int righttype;
public int getLefttype() {
return lefttype;
}
public void setLefttype(int lefttype) {
this.lefttype = lefttype;
}
public int getRighttype() {
return righttype;
}
public void setRighttype(int righttype) {
this.righttype = righttype;
}
public heroNode getLeftNode() {
return leftNode;
}
public void setLeftNode(heroNode leftNode) {
this.leftNode = leftNode;
}
public heroNode getRightNode() {
return rightNode;
}
public void setRightNode(heroNode rightNode) {
this.rightNode = rightNode;
}
public heroNode(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
@Override
public String toString() {
return "heroNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
public void setName(String name) {
this.name = name;
}
// Preorder traversal
public void PreOrder() {
System.out.println(this);
if (this.getLeftNode() != null) {
this.leftNode.PreOrder();
}
if (this.getRightNode() != null) {
this.rightNode.PreOrder();
}
}
// Middle order traversal
public void infixOrder() {
if (this.leftNode != null) {
this.leftNode.infixOrder();
}
System.out.println(this);
if (this.rightNode != null) {
this.rightNode.infixOrder();
}
}
// Postorder traversal
public void postOrder() {
if (this.leftNode != null) {
this.leftNode.postOrder();
}
if (this.rightNode != null) {
this.rightNode.postOrder();
}
System.out.println(this);
}
// Preorder search
public heroNode PreOrderSearch(int no) {
System.out.println("Preorder search");
//Compare whether the no of the current node is what we want to search
if (this.id == no) {
return this;
}
//Node to return
heroNode resNode = null;
// Judge whether the node on the left is empty. If it is not empty, recursive preamble search is performed
// If found, return the found node
if (this.leftNode != null) {
resNode = this.leftNode.PreOrderSearch(no);
}
//If it is not null, it means that if it is found on the left, it can be returned directly
if (resNode != null) {
return resNode;
}
// Judge whether the node on the right is empty. If it is not empty, recursive preamble search is performed
// If found, return the found node
if (this.rightNode != null) {
resNode = this.rightNode.PreOrderSearch(no);
}
return resNode;
}
// Medium order search
public heroNode infixOrderSearch(int no) {
//Node to return
heroNode resNode = null;
// Judge whether the left node is empty. If it is not empty, search in recursive order
// If found, return the found node
if (this.leftNode != null) {
resNode = this.leftNode.infixOrderSearch(no);
}
//If it is not null, it means that if it is found on the left, it can be returned directly
if (resNode != null) {
return resNode;
}
//Compare whether the no of the current node is what we want to search
System.out.println("Medium order search");
if (this.id == no) {
return this;
}
// Judge whether the node on the right is empty. If it is not empty, search in recursive order
// If found, return the found node
if (this.rightNode != null) {
resNode = this.rightNode.infixOrderSearch(no);
}
return resNode;
}
// Sequential search
public heroNode postOrderSearch(int no) {
//Node to return
heroNode resNode = null;
// Judge whether the node on the left is empty. If it is not empty, it will be searched recursively
// If found, return the found node
if (this.leftNode != null) {
resNode = this.leftNode.postOrderSearch(no);
}
//If it is not null, it means that if it is found on the left, it can be returned directly
if (resNode != null) {
return resNode;
}
// Judge whether the node on the right is empty. If it is not empty, it will be searched recursively
// If found, return the found node
if (this.rightNode != null) {
resNode = this.rightNode.postOrderSearch(no);
}
//If it is not null, it means that if it is found on the right, it can be returned directly
if (resNode != null) {
return resNode;
}
System.out.println("Sequential search");
//If the left and right subtrees are not found, then compare whether the no of the current node is what we want to search
if (this.id == no) {
return this;
}
return resNode;
}
// delete
public void deleteNode(int no) {
// Traverse to the left. If the left subtree is a little, set the left subtree empty. If not, traverse the right
if (this.leftNode != null && this.leftNode.id == no) {
this.leftNode = null;
return;
}
// Traverse to the right. If the right subtree is a little, set the left subtree empty. If there is no ready left or right, it should be deleted recursively
if (this.rightNode != null && this.rightNode.id == no) {
this.rightNode = null;
return;
}
// If the above two steps are unsuccessful, let's delete recursively to the left first
if (this.leftNode != null) {
this.leftNode.deleteNode(no);
}
// If the recursive deletion of the left subtree is not successful, the right subtree will be deleted recursively
if (this.rightNode != null) {
this.rightNode.deleteNode(no);
}
}
}Traversal cued binary tree
- Description: traverse the binary tree of middle order cueing in front
- Analysis: because the direction of each node changes after cueing, the original traversal method cannot be used. At this time, a new traversal method needs to be used Cued binary tree, each node can be traversed by linear way, so there is no need to use recursive way, which also improves the efficiency of traversal. The order of traversal should be consistent with that of middle order traversal.
public void preThreaddeList() {
// Here we need a variable to store the current node
heroNode tempNode = head;
while (tempNode != null) {
/* Start loop traversal
* Loop to find the node with lefttype 1, so the first one to find is the node with node value of 8
* Later, it will change with traversal. When lefttype ==1 is found, it indicates that the tree has been cued
* After that, you only need to deal with the effective nodes after cueing
* */
while (tempNode.getLefttype() == 0) {
System.out.println(tempNode);
tempNode = tempNode.getLeftNode();
}
// Because it is a medium order traversal, the order is: left, middle and right. Here, we are from the left lefttype==1, that is, it is the first node at the beginning of the left, so we can output it directly
System.out.println(tempNode);
// Traversal of this node
tempNode = tempNode.getRightNode();
}
}