brief introduction

Tree is a data structure similar to linked list. Different from the linear structure of linked list, tree is a nonlinear data structure with hierarchical structure.

The tree is composed of many nodes, and each node can point to many nodes.

If each node in a tree has only 0, 1 and 2 child nodes, the tree is called a binary tree. If we sort the binary tree.

For example, for each node in a binary tree, if the elements of the left subtree node are smaller than the root node and the elements of the right subtree node are larger than the root node, such a tree is called a Binary Search Tree (BST).

Today, let's discuss the properties of BST and the basic operation of BST.

Basic properties of BST

We have just talked about the basic features of BST, now let's summarize:

1. The left subtree of any node in the BST must be smaller than the value of the node
2. The right subtree of any node in BST must be larger than the value of this node
3. The left and right subtrees of any node in a BST must be a BST.

Look at a picture and feel BST intuitively:

Construction of BST

How to build a BST with code?

First of all, the BST is composed of nodes one by one. In addition to saving Node data, the Node node also needs to point to the left and right child nodes, so that our BST can be connected by nodes.

In addition, we also need a root node to represent the root node of BST.

The corresponding codes are as follows:

public class BinarySearchTree {

    //Root node
    Node root;

    class Node {
        int data;
        Node left;
        Node right;

        public Node(int data) {
            this.data = data;
            left = right = null;
        }
    }
}

BST search

Let's first look at the BST search. If it is the above BST, what steps should we take to search 32 this node?

Start with the above figure:

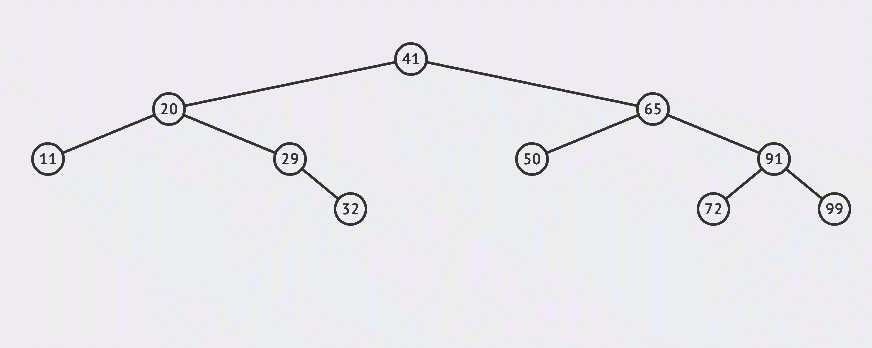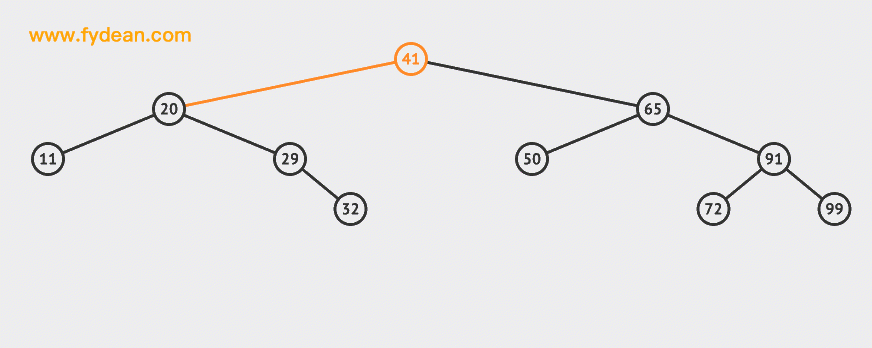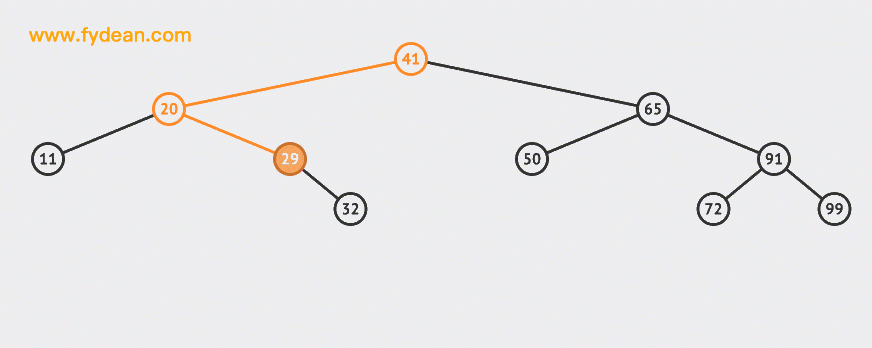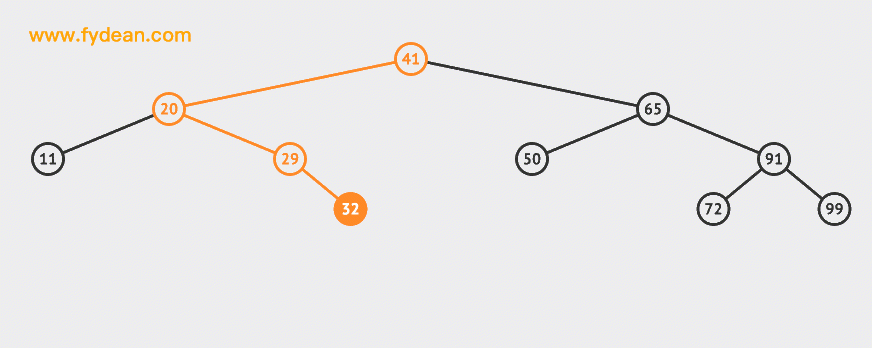
The basic steps of searching are:

1. Starting from the root node 41, compare the size of the root node and the search value
2. If the search value is less than the node value, the left tree is searched recursively
3. If the search value is greater than the node value, the right tree is searched recursively
4. If the nodes match, you can return directly.

The corresponding java code is as follows:

//The search method is from the root node by default
    public Node search(int data){
        return search(root,data);
    }

    //Recursive search node
    private Node search(Node node, int data)
    {
        // If the nodes match, the node is returned
        if (node==null || node.data==data)
            return node;

        // If the node data is larger than the data to be searched, continue to search the left node
        if (node.data > data)
            return search(node.left, data);

        // If the node data is smaller than the data to be searched, continue to search the right node
        return search(node.right, data);
    }

Insertion of BST

After the search, let's talk about BST insertion.

Let's start with an animation:

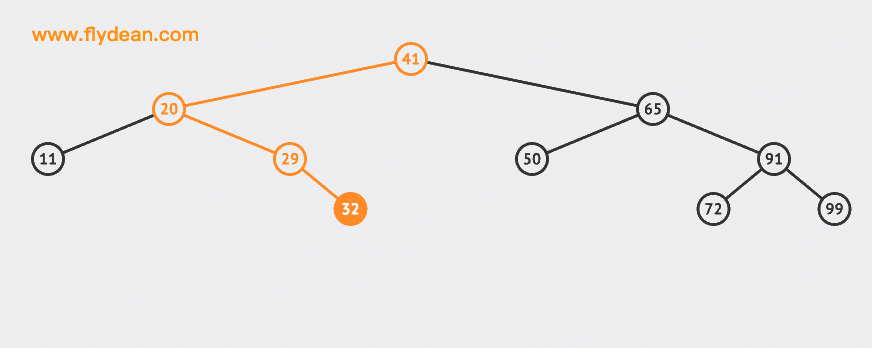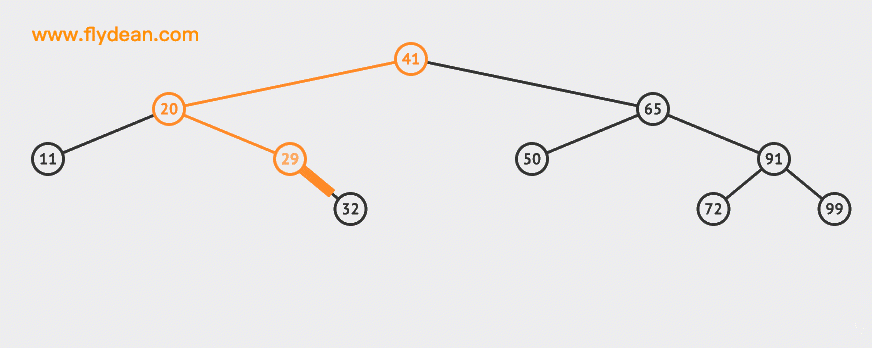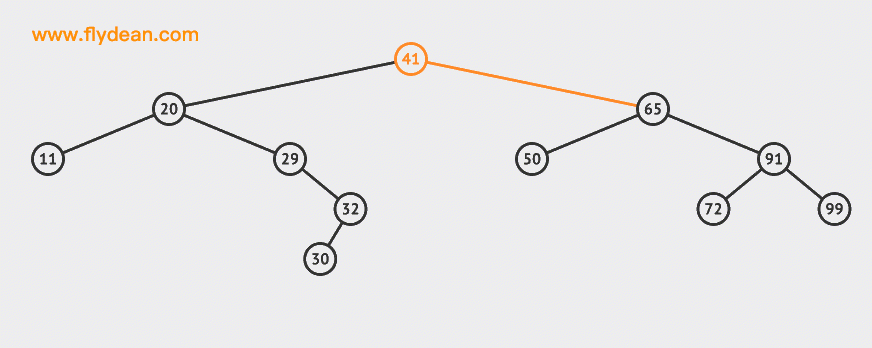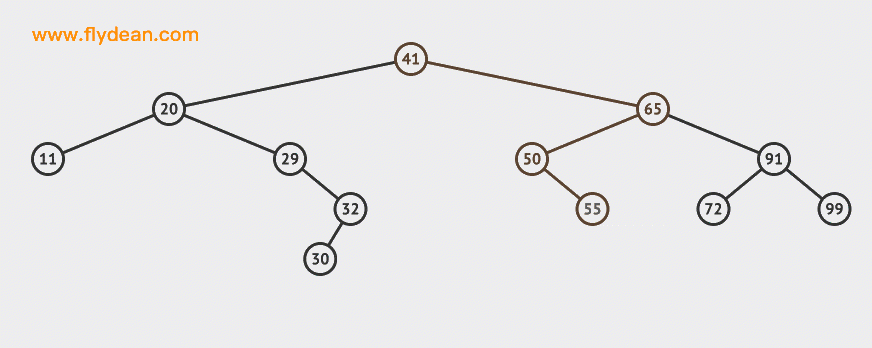
In the example above, we insert two nodes 30 and 55 into the BST.

The logic of insertion is as follows:

1. Starting from the root node, compare the node data with the data to be inserted
2. If the data to be inserted is less than the node data, the recursive left subtree is inserted
3. If the data to be inserted is larger than the node data, the recursive right subtree is inserted
4. If the root node is empty, the current data is inserted as the root node

The corresponding java code is as follows:

// Insert a new node, starting from the root node
    public void insert(int data) {
        root = insert(root, data);
    }

    //Insert new node recursively
    private Node insert(Node node, int data) {

        //If the node is empty, a new node is created
        if (node == null) {
            node = new Node(data);
            return node;
        }

        //If the node is not empty, it is compared to recursively insert left or right
        if (data < node.data)
            node.left = insert(node.left, data);
        else if (data > node.data)
            node.right = insert(node.right, data);

        //Returns the inserted node
        return node;
    }

Deletion of BST

The deletion of BST is a little more complicated than insertion, because insertion is always inserted into leaf nodes, while deletion may delete non leaf nodes.

Let's take a look at an example of deleting a leaf node:

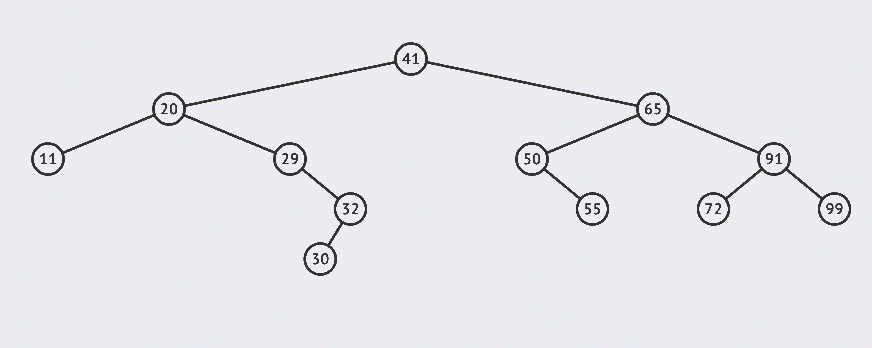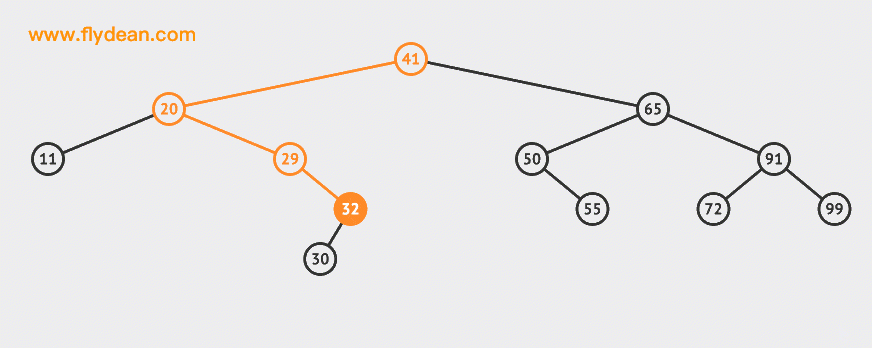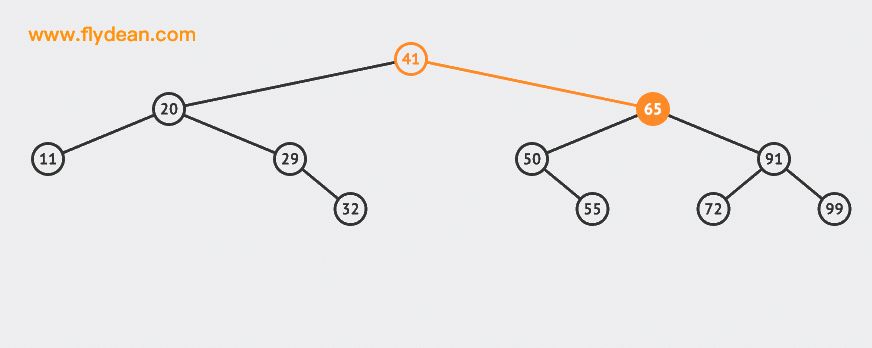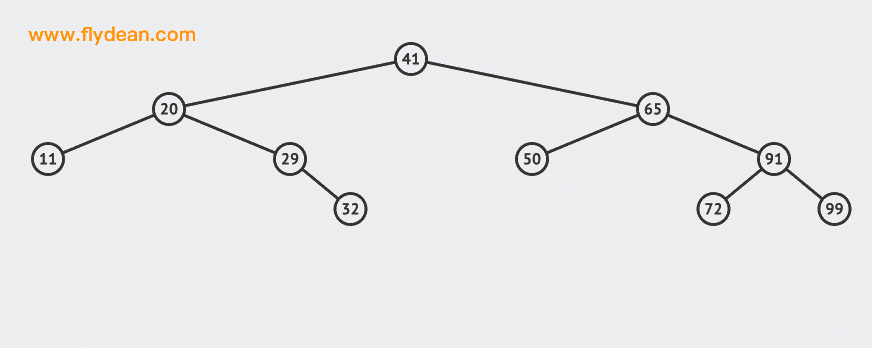
In the above example, we deleted 30 and 55 nodes.

It can be seen that deleting leaf nodes is relatively simple. You can delete them after finding them.

Let's take a more complex example. For example, we want to delete 65 this node:

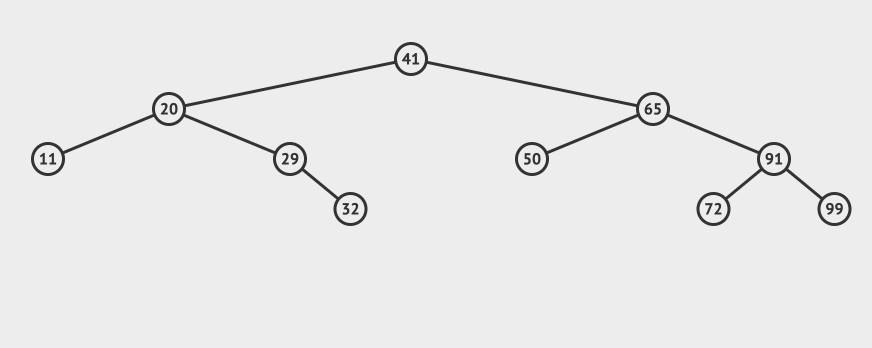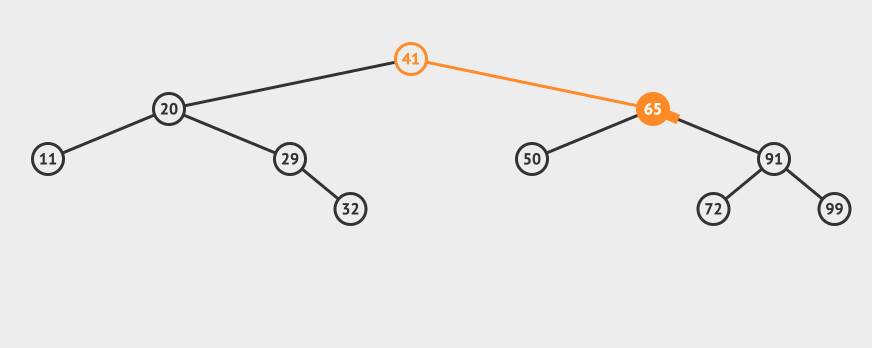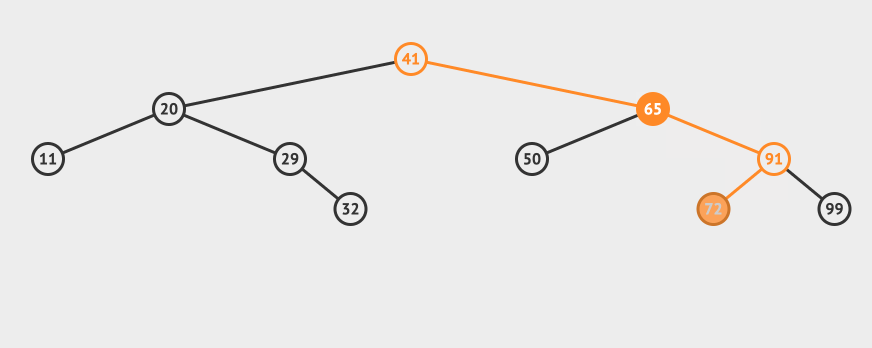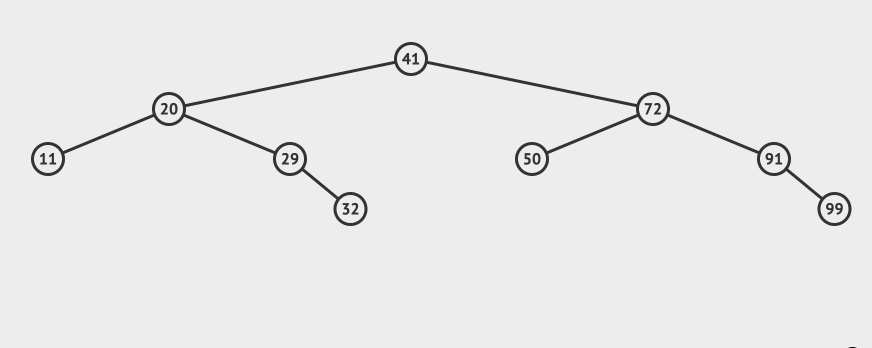
You can see that you need to find the smallest one in the right subtree of node 65 and replace node 65 (of course, you can also find the largest one in the left subtree).

So the deletion logic is as follows:

1. Starting from the root node, compare the size of the node to be deleted and the root node
2. If the node to be deleted is smaller than the root node, the left subtree is deleted recursively
3. If the node to be deleted is larger than the root node, the right subtree is deleted recursively
4. If the nodes match, there are two more cases
5. If it is a single-sided node, return directly to the other side of the node
6. If it is a bilateral node, first find the minimum value on the right as the root node, and then delete the node on the right after the minimum value as the right node of the root node

Let's look at the implementation of the code:

 // Delete the new node, starting from the root node
    void delete(int data)
    {
        root = delete(root, data);
    }

    //Recursively delete nodes
    Node delete(Node node, int data)
    {
        //If the node is empty, return directly
        if (node == null)  return node;

        //Traverse the left and right nodes
        if (data < node.data)
            node.left = delete(node.left, data);
        else if (data > root.data)
            node.right = delete(node.right, data);

        //If the nodes match
        else
        {
            //If it is a unilateral node, the node below it is returned directly
            if (node.left == null)
                return node.right;
            else if (node.right == null)
                return node.left;

            //If it is a bilateral node, first find the minimum value on the right as the root node, and then delete the node on the right after the minimum value as the right node of the root node
            node.data = minValue(node.right);

            // Delete the smallest node from the right
            node.right = delete(node.right, node.data);
        }
        return node;
    }

Here we use recursion to delete bilateral nodes. Can you consider whether there are other ways to delete them?