Cantor expansion:

Cantor expansion example:
Give an example.
In the permutation and combination of 5 numbers, the Cantor expansion value of 3452 is calculated.
{1,2,3,4,5}:
If the first is 3, then there are two numbers less than 3, then a[5]=2;
{1,2,4,5}:
The second is 4. There are only 2 smaller than 4, so a[4]=2;
{1,2,5}
The third digit is 1. There are 0 numbers less than 1, so a[3]=0.
{2,5}
The fourth digit is 5, and there is 1 number less than 5, so a[2]=1;
The last bit does not need to be calculated, because there is no number after it, a[1]=0;
According to the formula:
a[5]*4!+a[4]*3!+a[3]*2!+a[2]1!+00!=61;
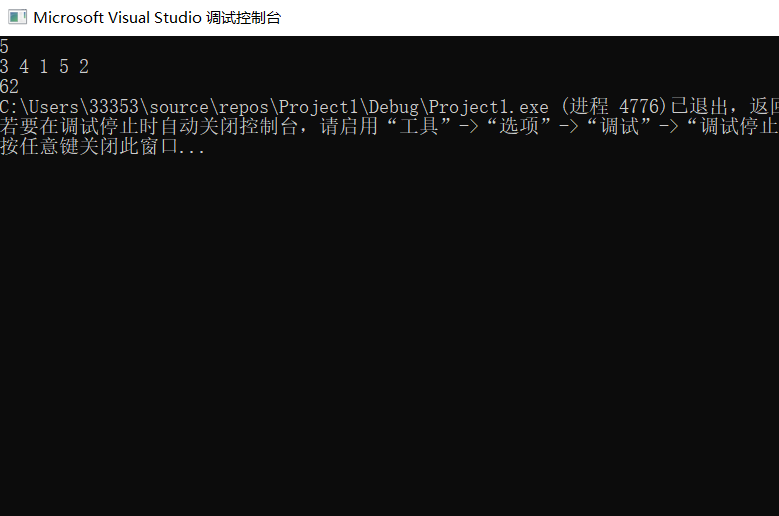
Therefore, there are 61 combinations smaller than 3452, that is, 3452 is the 62nd. (12345 is the first combination}
1. Change the number into several combinations:

#include<iostream>
using namespace std;
const int factorial[] = { 1,1,2,6,24,120,720,5040,40320,362880,3628800 };//Factorial 0-10
int cantor(int a[], int n) {//cantor expansion, n represents the full permutation of N bits, and a [] represents the number of full permutations (represented by an array)
	int ans = 0, sum = 0;
	for (int i = 1; i < n; i++) {
		for (int j = i + 1; j <= n; j++)
		{
			if (a[j] < a[i])
				sum++;
			ans += sum * factorial[n - i];//accumulate
			sum = 0;//Counter zeroing
		}
	}
	return ans + 1;
}
int main() {
	int sb[12], gs;
	cin >> gs;//digit
	for (int i = 1; i <= gs; i++)
		cin >> sb[i];//Number of to test
	cout << cantor(sb, gs);//Output the position of the set in the full arrangement 
	return 0;
}

Input:
5
3 4 1 5 2
Output:

Inverse operation
{1,2,3,4,5}
Use 61 / 4! = 2 + 13, indicating that there are 2 numbers smaller than the first, so the first is 3.
{1,2,4,5}
Use 13 / 3! = 2 + 1, indicating that there are 2 numbers less than the second digit, so the second digit is 4.
{1,2,5}
Use 1 / 2! = 0 + 1, indicating that there is no number less than the third digit, so the third digit is 1.
{2,5}
Use 1 / 1! = 1 + 0, indicating that there is 1 less than the fourth digit, so the fourth digit is 5.
{2}
The last one is naturally the remaining number 2.
2. Change the combined digits into numbers

#include<iostream>
using namespace std;
const int FAC[] = { 1,1,2,6,24,120,720,5040,40320,364880 };
bool used[11]={0};
void rule(int n,int sum)
{
	//cout << sum << endl;
	int flag1, flag2;//Record quotient and remainder
	for (int i = sum-1; i >= 0; i--)
	{
		flag1 = n / FAC[i];
		flag2 = n % FAC[i];
		//cout << flag1 << "   " << flag2 << endl;
		int amount = 0;
		int j;
		for (j = 0; j <=flag1; j++)
		{
			if (used[j])
				flag1++;
		}
		cout << flag1 + 1 << " ";
		used[flag1] = 1;
		n = flag2;
	}
}
int main()
{
	int n;//Input 62, output 34152;
	int sum;//Number of digits;
	cin >> sum;
	cin >> n;
	rule(n,sum);
	return 0;
}

Input: 5
62
Output: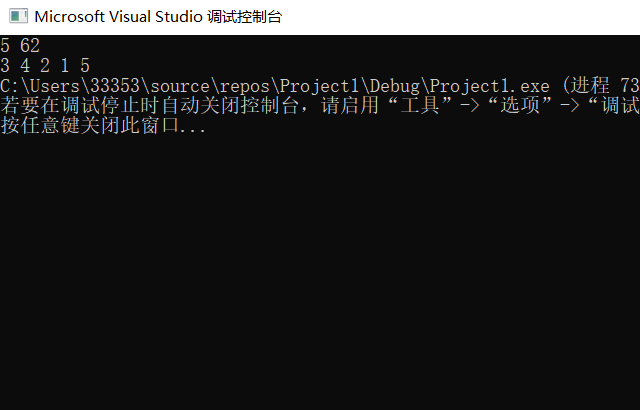

Los Angeles P1088: Martians

Title:
A Martian demonstrated how to count with fingers with a human hand. If the five fingers - thumb, index finger, middle finger, ring finger and little finger are numbered 1,2,3,4 and 5 respectively, when they are arranged in normal order, they form five digits 12345. When you exchange the positions of ring finger and little finger, they form five digits 12354. When you completely change the order of five fingers When inverted, 54321 will be formed. Among all the 120 5 digits that can be formed, 12345 is the smallest, which represents 1; 12354 is the second smallest, which represents 2; 54321 is the largest, which represents 120.

A number represented by a ternary number
123 1
132 2
213 3
231 4
312 5
321 6

Your task is to add the number represented by Martian fingers to the number told by scientists, and change the order of Martian fingers according to the addition result. Input data to ensure that the result will not exceed the range that Martian fingers can represent.
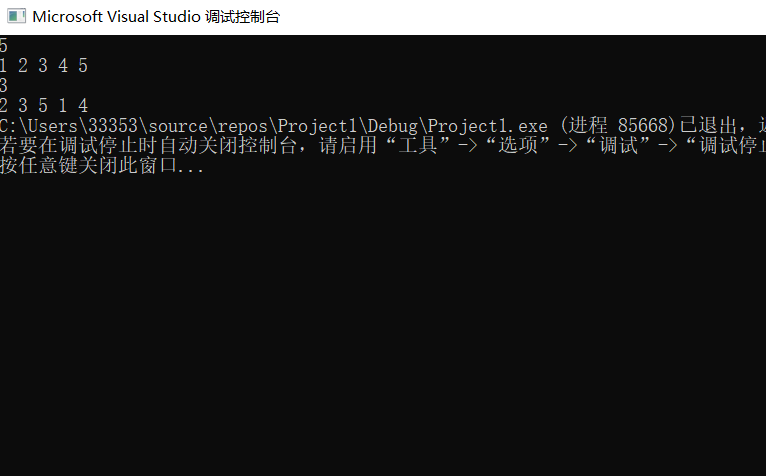
Input:
5
3
1 2 3 4 5
Output:
1 2 4 5 3

Problem solving: it was convenient to solve the problem with STL at the beginning, but it always timed out. Therefore, after reading the problem solving, I found a method of variable base, so I went to understand Cantor expansion and found that his method was optimized on the basis of Cantor expansion. Cantor expansion on Baidu uses order multiplication to calculate the number of digits of 61. If the number is a little larger, the calculation will be doubled, but He directly adopts a method of binary conversion, and the code is very exquisite. I also use a little binary conversion in the inverse operation.
What about him? Take 34152 as an example.
{1,2,3,4,5}:
If the first is 3, then there are two numbers less than 3, then a[5]=2;
{1,2,4,5}:
The second is 4. There are only 2 smaller than 4, so a[4]=2;
{1,2,5}
The third digit is 1. There are 0 numbers less than 1, so a[3]=0.
{2,5}
The fourth digit is 5, and there is 1 number less than 5, so a[2]=1;
The last bit does not need to be calculated, because there is no number after it, a[1]=0;
So we get the number: {2,2,0,1,0}
So how do you calculate the last three digits
Add three
{2,2,0,1,3} - "the decimal places are {5,4,3,2,1}
{2,2,0,3,1}
{2,2,1,1,1}
Then the key highlight is the code;

#include<iostream>
using namespace std;
int a[10005];
bool used[10005] = { 0 };
int m, n;
int main()
{
	cin >> n >> m;
	//Positive operation
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
		int x = a[i];
		for (int j = 1; j <= a[i]; j++)
			x -= used[j];
		used[a[i]] = 1;//Remove the used number
		a[i] = x - 1;
	}
	a[n] += m;
	//Conversion base
	for (int i = n; i > 0; i--)
	{
		a[i - 1] += a[i] / (n - i + 1);
		a[i] %= n - i + 1;
	}
	//Inverse operation
	memset(used, 0, sizeof(used));
	for (int i = 1; i <= n; i++)
	{
		for (int j = 0; j <= a[i]; j++)
			if (used[j])
				a[i]++;
		cout << a[i] + 1 << " ";
		used[a[i]] = 1;
	}
	return 0;
}

1. Positive operation:
1. For 3, the number smaller than three should be two, and the previous number has not been used, then the number is 2
2. As far as 4 is concerned, the number smaller than 4 should be three, and then the first three is used and subtracted to 2
Push in with this.
2. Inverse operation:
1. For the first 2, there are two numbers less than, that is, three. If there are all the preceding numbers, it is three.
2. For the second 2, there are two numbers less than, that is, three. If there are three in front, the range to be found will be moved back one, so a[i] + +; so the second is 4
Push in with this.
Operation results:

Part of the content comes from Baidu and Luogu solutions.