Machine Learning A-Z learning notes 16 Thompson sampling algorithm

1. Simple principle

This paper continues to talk about a reinforcement learning algorithm called Thompson sampling algorithm. The mathematical theoretical basis of this algorithm is Bayesian inference. Let's talk about the basic principle of this algorithm first, also taking the multi arm slot machine as an example

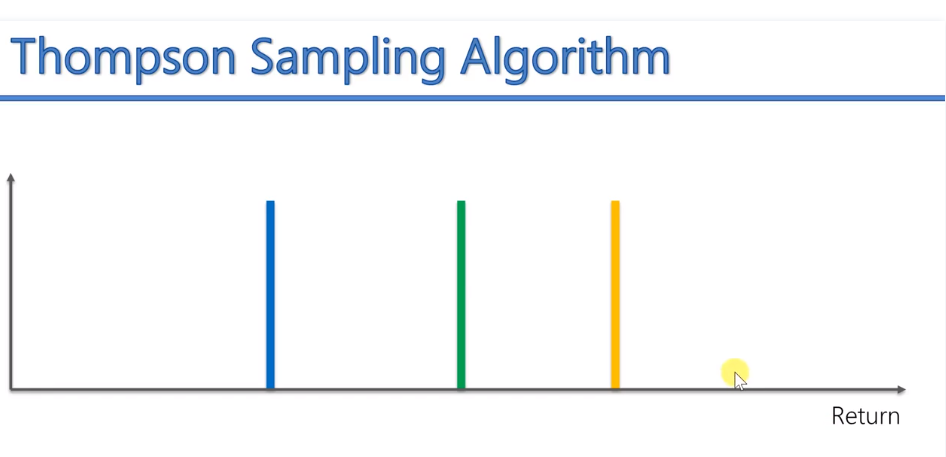
Calculation flow of sampling algorithm

As shown in the figure, the horizontal axis represents rewards, and the more to the right, the more rewards. Three vertical lines represent three different slot machines and their average rewards.

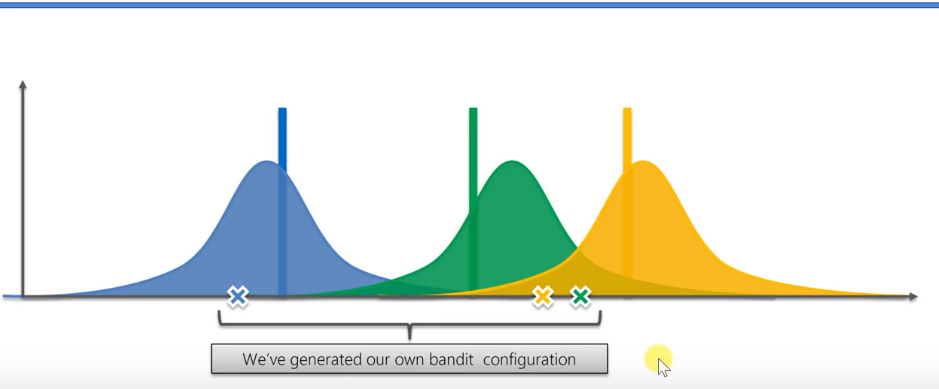
Before the algorithm starts, we don't know anything, so we need to get some basic data. According to the data of four slot machines, you can get several rewards according to the blue distribution. Similarly, a green slot machine can also get a distribution, and the same is true for yellow.

These three distributions predict the probability distribution of the mathematical expectation that the three machines bring us rewards. Next, based on these three random distributions, we get several random samples. Select the machine that obtains the maximum sampling value and press it. However, because it is random, although the actual expectation of yellow is the highest, we may still choose a result in which green is greater than yellow.

After pressing it, we will get a new observed reward value. After getting the new reward value, we need to adjust the distribution of green machines.

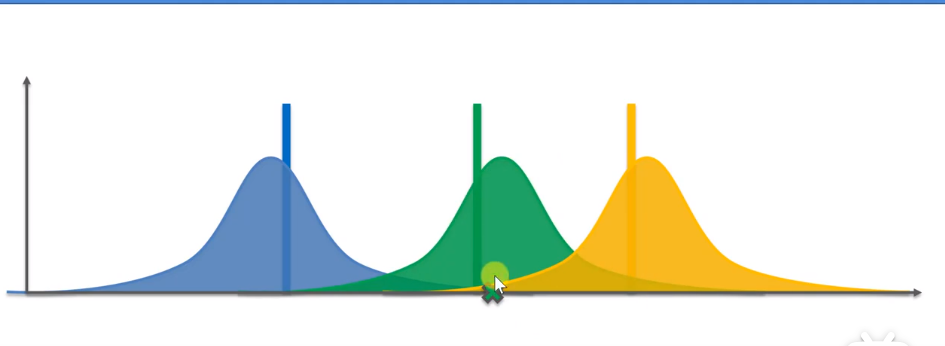
Obviously, the green distribution becomes higher and narrower. The following steps are actually the same as here. Still select the machine with the highest reward value, press it, and continue to adjust the distribution through the results obtained.

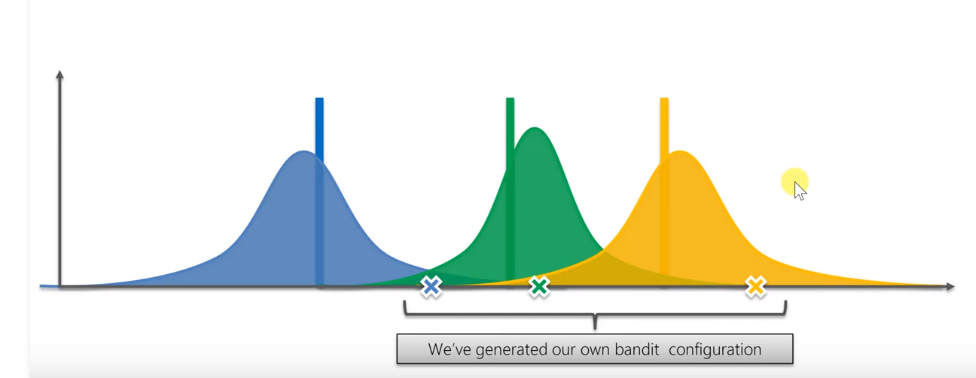
When the game goes through many steps, these distributions will become very narrow, especially the yellow ones will basically match the actual expectations

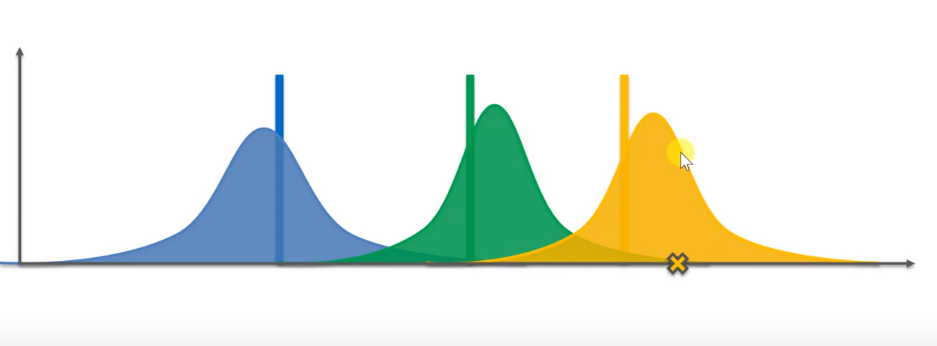
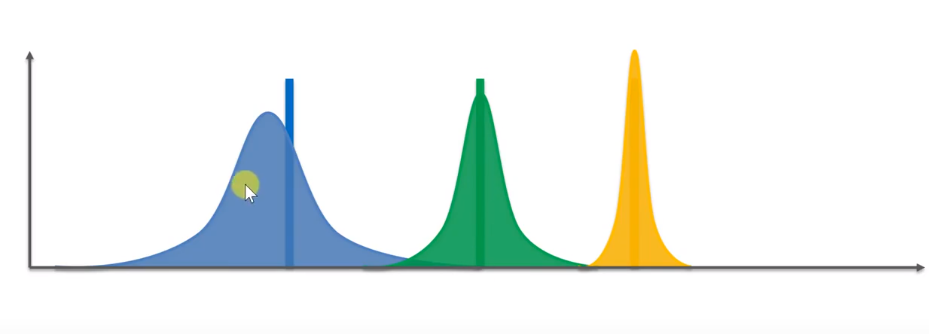
At this time, because we always choose the machine with the highest reward value, the probability of pressing yellow will be relatively high, resulting in that the yellow one will be narrower and narrower, while the blue one is rarely played, so it should be relatively wider.

Thompson sampling algorithm vs. upper bound algorithm of confidence interval

We use Thompson sampling algorithm and ucb algorithm to deal with the multi arm slot machine problem. Now let's compare the next two algorithms. Let's take a look at the basic schematic diagram of these two algorithms.

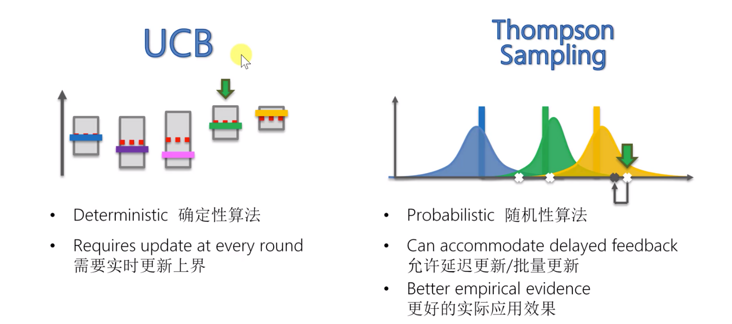
First of all, this UCB algorithm is a deterministic algorithm. When we get the same reward, our decisions are determined. Therefore, our total income and total income in each round are determined. The decision made in each round is only related to the upper bound of the confidence interval, which is only related to all the observations of the machine. So when the observation values of all machines are the same, we will always make the same decision. For Thompson algorithm, it is a random algorithm. One or more of its steps are controlled by a random function, which is related to luck. It depends on some random events. For example, when we select points above, although the actual expectation of yellow is greater than that of green, we may still select data points where green is greater than yellow. Therefore, it is a random algorithm.

Another feature of UCB is that it needs to update the upper bound in real time, which can be seen when describing the principle of UCB algorithm in previous articles. For Thompson sampling algorithm, it allows delayed updates or even batch updates. For example, we put a batch of advertisements on the Internet. Here, it is allowed to get delayed results. Finally, in the practical application and research in recent years, it is found that Thompson sampling algorithm has better practical application effect than confidence interval algorithm.

2. Relevant codes

# Thompson Sampling

# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# Importing the dataset
dataset = pd.read_csv('Ads_CTR_Optimisation.csv')

# Implementing Thompson Sampling
import random
N = 10000
d = 10
ads_selected = []
numbers_of_rewards_1 = [0] * d
numbers_of_rewards_0 = [0] * d
total_reward = 0
for n in range(0, N):
    ad = 0
    max_random = 0
    for i in range(0, d):
        # The probability of generating this round of advertisements i (by accumulating the number of clicks and the number of non clicks, and based on Bayesian inference)
        random_beta = random.betavariate(numbers_of_rewards_1[i] + 1, numbers_of_rewards_0[i] + 1)
        # If the advertising i probability is the highest in this round, it is selected to push
        if random_beta > max_random:
            max_random = random_beta
            ad = i
    # Log record
    ads_selected.append(ad)
    # Confirm the customer's click results
    reward = dataset.values[n, ad]
    # If i is updated, i is the cumulative number of reading points
    if reward == 1:
        numbers_of_rewards_1[ad] = numbers_of_rewards_1[ad] + 1
    # If the click result is 1, the cumulative number of ads i that are not clicked will be updated
    else:
        numbers_of_rewards_0[ad] = numbers_of_rewards_0[ad] + 1
    #Update total Awards
    total_reward = total_reward + reward

# Visualising the results - Histogram
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()