catalogue
2, Simple application examples of Bayesian classifier
3, Spam filtering using naive Bayes
3.1 cut the text into vectors, store them in the list, and classify and label the vocabulary vectors
3.2. Create a vocabulary and convert the segmented entries into entry vectors.
3.3. Training naive Bayesian classifier through entry vector
3.4. Train the classifier, and then use the classifier for classification.
4.1. Some advantages of naive Bayesian inference:
4.2. Some disadvantages of naive Bayesian inference:
1, Naive Bayesian concept
Naive Bayes is a classification algorithm based on probability theory. Based on Bayesian theory, it classifies by calculating the probability that samples belong to different categories. It is a classical classification algorithm. Naive Bayes is a method in Bayesian classifier. It is called naive because it adopts the assumption that all feature conditions are independent.
Bayesian theory is an effective method to calculate the degree of belief (or hypothesis, proposition, proposition) based on the best evidence available (observation, data and information, etc.). The degree of belief is the confidence in the authenticity and correctness of things. The core of naive Bayes is naive Bayes formula. Before understanding naive Bayes formula, you might as well understand the related concepts such as conditional probability, full probability formula, a priori probability and a posteriori probability.
1.1 conditional probability
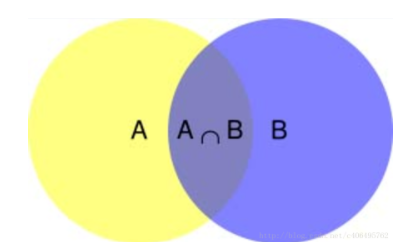
As shown in the figure above, it can be clearly seen that when event B occurs, the probability of event A is P(A ∩ B) divided by P(B).
Namely:
Therefore:
Similarly:
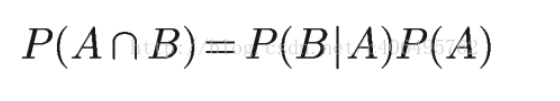
So:
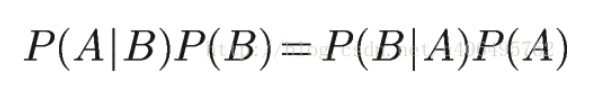
Thus, it can be deduced that:
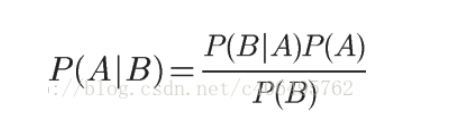
The above is the calculation formula of conditional probability.
1.2 full probability formula
Suppose that the sample space S is the sum of two events A and A '.
In the above figure, the red part is event A, and the yellow green part is event A ', which together constitute the sample space S.
In this case, event B can be divided into two parts.
Namely:
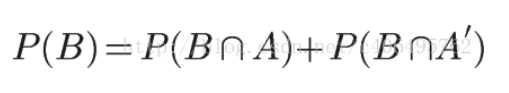
Because:
So:
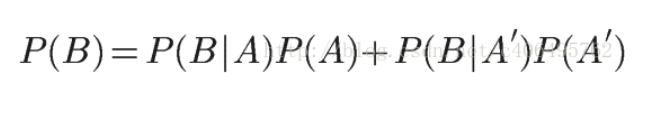
For example, chestnuts:
1.3 Bayesian inference
By modifying the conditional probability formula:
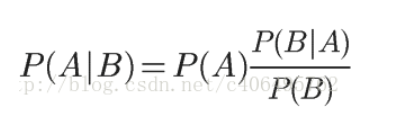
2, Simple application examples of Bayesian classifier
When buying fruit in the supermarket, apples are often necessary. Over the years, I have explored a set of methods to select apples. Generally, the ruddy and smooth fruits are good apples, and the green and irregular ones are generally ordinary. Now, according to the apples I bought several times, 10 apples have been verified, and the good and bad are distinguished mainly according to the three characteristics of size, color and shape, as follows:
The characteristics of an apple I am about to buy in the supermarket are as follows:
size colour shape Good fruit
large gules circular ？
Q: is it a good fruit or an ordinary apple? What is the probability according to the existing data set?
A priori probability P(c), simplified solution: divide the number of class C samples by the number of all samples, so:
P(c = good fruit)= 4/10
P(c = General) = 6 / 10
The class conditional probability of each attribute can be preliminarily solved by dividing the number of samples corresponding to this attribute in the samples under this category by the number of samples under this category. Therefore:
P (size = large | c = good fruit)= 3/4
P (color = red | c = good fruit) = 4 / 4
P (shape = round | c = good fruit) = 3 / 4
P (size = large | c = average)= 3/6
P (color = red | c = General) = 1 / 6
P (shape = circular | c = General)= 2/6
Therefore:
P(c = good fruit) * P (size = big | c = good fruit) * P (color = red | c = good fruit) * P (shape = round | c = good fruit)
= 4/10 * 3/4 * 4/4 * 3/4
= 0.225
P(c = General) * P (size = large | c = General) * P (color = red | c = General) * P (shape = round | c = General)
= 6/10 * 3/6 * 1/6 * 2/6
= 0.0167
Obviously, 0.225 > 0.0167 So: this apple is a good fruit.
3, Spam filtering using naive Bayes
3.1 cut the text into vectors, store them in the list, and classify and label the vocabulary vectors
def loadDataSet():
postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], #Segmented entry
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0,1,0,1,0,1] #Category label vector, 1 for insulting words, 0 for not
return postingList,classVec
if __name__ == '__main__':
postingLIst, classVec = loadDataSet()
for each in postingLIst:
print(each)
print(classVec)
3.2. Create a vocabulary and convert the segmented entries into entry vectors.
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0] * len(vocabList) #Create a vector with 0 elements
for word in inputSet: #Traverse each entry
if word in vocabList: #If the entry exists in the vocabulary, set 1
returnVec[vocabList.index(word)] = 1
else: print("the word: %s is not in my Vocabulary!" % word)
return returnVec #Return document vector
def createVocabList(dataSet):
vocabSet = set([]) #Create an empty non repeating list
for document in dataSet:
vocabSet = vocabSet | set(document) #Union set
return list(vocabSet)
if __name__ == '__main__':
postingList, classVec = loadDataSet()
print('postingList:\n',postingList)
myVocabList = createVocabList(postingList)
print('myVocabList:\n',myVocabList)
trainMat = []
for postinDoc in postingList:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
print('trainMat:\n', trainMat)
postingList is the original entry list and myVocabList is the vocabulary. myVocabList is the collection of all words that appear without duplicate elements. If a word appears once in the vocabulary, it will be recorded as 1 in the corresponding position. If it does not appear, it will be recorded as 0 in the corresponding position.
3.3. Training naive Bayesian classifier through entry vector
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix) #Calculate the number of training documents
numWords = len(trainMatrix[0]) #Calculate the number of entries per document
pAbusive = sum(trainCategory)/float(numTrainDocs) #Probability that the document belongs to the insult class
p0Num = np.ones(numWords); p1Num = np.ones(numWords) #Create numpy.ones array, initialize the number of entries to 1, and Laplace smoothing
p0Denom = 2.0; p1Denom = 2.0 #Denominator initialized to 2, Laplace smoothing
for i in range(numTrainDocs):
if trainCategory[i] == 1: #The data required for statistics of conditional probability belonging to insult class, i.e. P(w0|1),P(w1|1),P(w2|1)···
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else: #The data required to count the conditional probability belonging to the non insult class, i.e. P(w0|0),P(w1|0),P(w2|0)···
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = np.log(p1Num/p1Denom) #Take logarithm to prevent lower overflow
p0Vect = np.log(p0Num/p0Denom)
return p0Vect,p1Vect,pAbusive #Return the conditional probability array belonging to insult class and the conditional probability array belonging to non insult class
if __name__ == '__main__':
postingList, classVec = loadDataSet()
myVocabList = createVocabList(postingList)
print('myVocabList:\n', myVocabList)
trainMat = []
for postinDoc in postingList:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V, p1V, pAb = trainNB0(trainMat, classVec)
print('p0V:\n', p0V)
print('p1V:\n', p1V)
print('classVec:\n', classVec)
print('pAb:\n', pAb)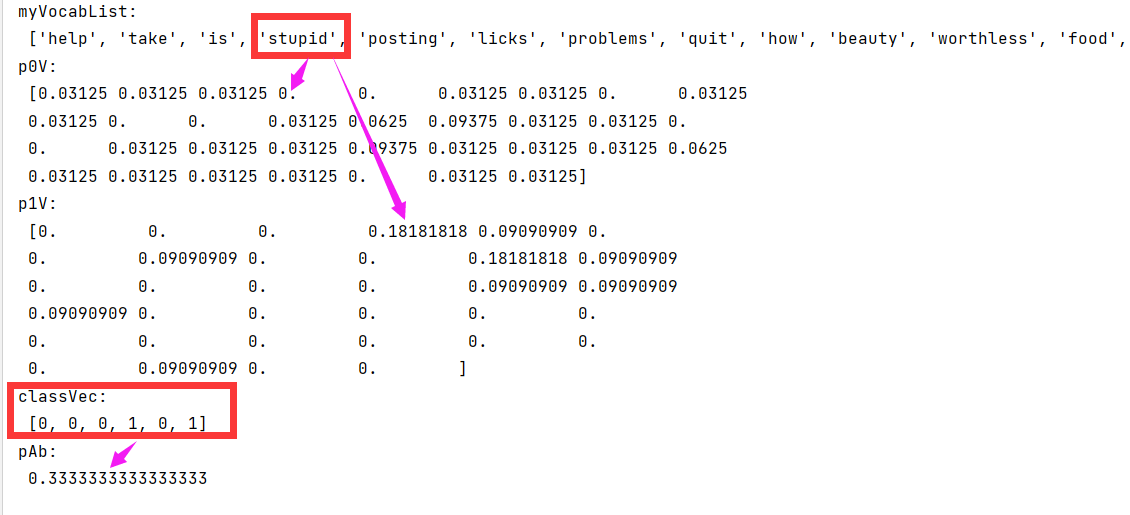
The running results are shown in the figure: p0V stores the probability that each word belongs to category 0, that is, non insulting words. p1V stores the probability that each word belongs to category 1, that is, insulting words. For example, the fourth stupid in the vocabulary, the probability of non insulting class is 0, and the probability of insulting class is 0.1818. pAb is the probability that all insulting classes account for all samples. It can be seen from classVec that there are two insulting classes, so the probability of pAb is 0.3333.
3.4. Train the classifier, and then use the classifier for classification.
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
p1 = sum(vec2Classify * p1Vec) + np.log(pClass1) #Multiply the corresponding elements. logA * B = logA + logB, so add log(pClass1) here
p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
def testingNB():
listOPosts,listClasses = loadDataSet() #Create experimental samples
myVocabList = createVocabList(listOPosts) #Create vocabulary
trainMat=[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) #Vectorization of experimental samples
p0V,p1V,pAb = trainNB0(np.array(trainMat),np.array(listClasses)) #Training naive Bayesian classifier
testEntry = ['love', 'my', 'home'] #Test sample 1
thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry)) #Test sample Vectorization
if classifyNB(thisDoc,p0V,p1V,pAb):
print(testEntry,'It belongs to the insult category') #Perform classification and print classification results
else:
print(testEntry,'It belongs to the non insulting category') #Perform classification and print classification results
testEntry = ['stupid', 'garbage'] #Test sample 2
thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry)) #Test sample Vectorization
if classifyNB(thisDoc,p0V,p1V,pAb):
print(testEntry,'It belongs to the insult category') #Perform classification and print classification results
else:
print(testEntry,'It belongs to the non insulting category') #Perform classification and print classification results
if __name__ == '__main__':
testingNB()
3.5 spam classification test
The data set is divided into training set and test set, and the accuracy of naive Bayesian classifier is tested by cross validation.
def textParse(bigString): #Convert string to character list
listOfTokens = re.split(r'\W*', bigString) #Use special symbols as segmentation marks to segment strings, that is, non alphabetic and non numeric
return [tok.lower() for tok in listOfTokens if len(tok) > 2] #Except for a single letter, such as a capital I, other words become lowercase
"""
Function description:Test naive Bayesian classifier
"""
def spamTest():
docList = []; classList = []; fullText = []
for i in range(1, 26): #Traverse 25 txt files
wordList = textParse(open('email/spam/%d.txt' % i, 'r').read()) #Read each spam and convert the string into a string list
docList.append(wordList)
fullText.append(wordList)
classList.append(1) #Mark spam, 1 indicates junk file
wordList = textParse(open(('email/ham/%d.txt' )% i, 'r').read()) #Read each non spam message and convert the string into a string list
docList.append(wordList)
fullText.append(wordList)
classList.append(0) #Mark non spam, 1 indicates junk file
vocabList = createVocabList(docList) #Create vocabulary without repetition
trainingSet = list(range(50)); testSet = [] #Create a list that stores the index values of the training set and the test set
for i in range(10): #From the 50 emails, 40 were randomly selected as the training set and 10 as the test set
randIndex = int(random.uniform(0, len(trainingSet))) #Random selection of index value
testSet.append(trainingSet[randIndex]) #Add index value of test set
del(trainingSet[randIndex]) #Delete the index value added to the test set in the training set list
trainMat = []; trainClasses = [] #Create training set matrix and training set category label coefficient vector
for docIndex in trainingSet: #Ergodic training set
trainMat.append(setOfWords2Vec(vocabList, docList[docIndex])) #Add the generated word set model to the training matrix
trainClasses.append(classList[docIndex]) #Add a category to the training set category label coefficient vector
p0V, p1V, pSpam = trainNB0(np.array(trainMat), np.array(trainClasses)) #Training naive Bayesian model
errorCount = 0 #Error classification count
for docIndex in testSet: #Traversal test set
wordVector = setOfWords2Vec(vocabList, docList[docIndex]) #Word set model of test set
if classifyNB(np.array(wordVector), p0V, p1V, pSpam) != classList[docIndex]: #If the classification is wrong
errorCount += 1 #Error count plus 1
print("Misclassified test sets:",docList[docIndex])
print('Error rate:%.2f%%' % (float(errorCount) / len(testSet) * 100))
if __name__ == '__main__':
spamTest()Operation results:
The function spamTest() outputs the probability of classification errors on 10 randomly selected emails. Since these emails are randomly selected, the output may be different each time. If an error is found, the function will output this table of the wrong document, so that you can know which document has the error. If you want to better estimate the error rate, you should repeat the above process several times, such as 10 times, and then average it. In contrast, it is better to misjudge spam as normal mail than to classify normal mail as spam.
IV. summary
4.1. Some advantages of naive Bayesian inference:
- Generative model, which classifies by calculating probability, can be used to deal with multi classification problems.
- It performs well on small-scale data, is suitable for multi classification tasks, is suitable for incremental training, and the algorithm is also relatively simple.
4.2. Some disadvantages of naive Bayesian inference:
- It is sensitive to the expression of input data.
- Due to the "simplicity" of naive Bayes, it will bring some loss of accuracy.
- A priori probability needs to be calculated, and there is an error rate in classification decision-making.