Reference resources:
https://cuijiahua.com/blog/2017/11/ml_4_bayes_1.html
https://cuijiahua.com/blog/2017/11/ml_5_bayes_2.html
https://www.jianshu.com/p/5953923f43f0

1, Brief introduction of naive Bayes

1.1 introduction to naive Bayesian algorithm

Naive Bayesian algorithm, which is based on the Bayesian algorithm, is simplified, that is, the attributes are assumed to be independent of each other when the target value is given.

1.2 Bayes theorem

Bayesian decision theory: choose the occurrence with high probability as the final judgment.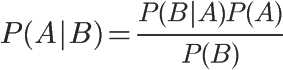

According to the known basic condition probability and partial probability, the probability under some conditions is deduced.

1.3 conditional probability inference

We can deduce the probability of A event under B condition, and then change A ∩ B to another representation step by step





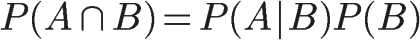
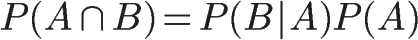
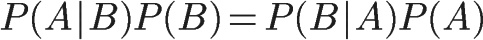
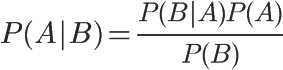
This is the formula of conditional probability.
If considering the following total probability formula and the above picture, only A and A 'conditional probability formula can be changed to: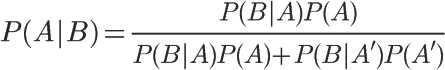

1.4. Full probability inference

If events A1, A2 An forms a complete event group, namely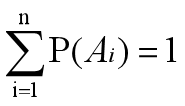

And all of them have positive probability, so for any event A, there is the following full probability formula: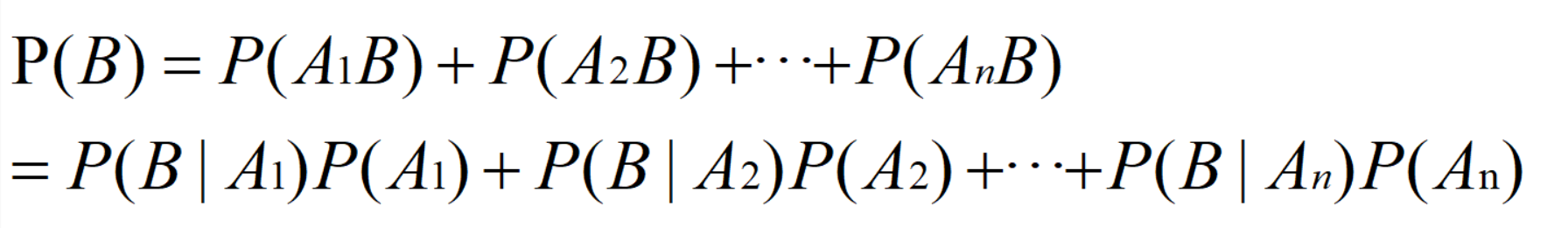

1.5 Bayesian inference

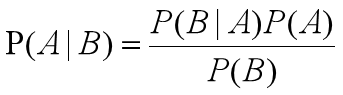
P(A) is called "Prior probability", that is, before the occurrence of event B, we judge the probability of event A.
P(A|B) is called "Posterior probability", that is, after the occurrence of event B, we reevaluate the probability of event A.
P(B|A)/P(B) is called "Likelyhood", which is an adjustment factor to make the estimated probability closer to the real probability.

Therefore, the conditional probability can be understood as the following formula:
Posterior probability = prior probability x adjustment factor

1.6 Laplacian smoothing

When maximum likelihood estimation is used, some values of the possible characteristic X(j) do not appear in the sample of Ck label. At this time, the likelihood function is 0, and the target function is 0, which will lead to the deviation of classification. To solve this problem, Bayesian estimation is used: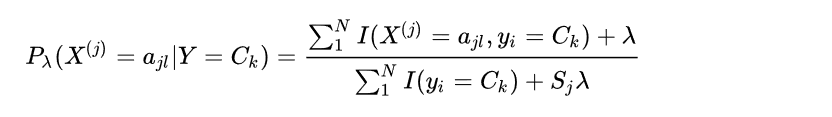
Where Sj is the number of non repeated values of the j-th feature in the Ck tag. When λ = 0 is the maximum likelihood estimation, when λ = 1, it is called Laplacian smoothing. Similarly, the Bayesian estimation of prior probability is: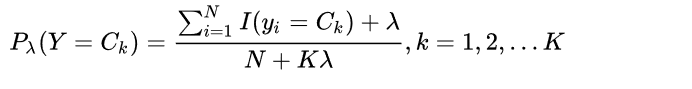

Two, example

2.1 example explanation

Take online community message as an example. In order not to affect the development of the community, we need to block insulting speech, so we need to build a fast filter. If a message uses negative or insulting language, it will be marked as inappropriate content. Filtering such content is a common requirement. There are two types of this problem: insulting and non insulting, which are represented by 1 and 0 respectively.

# Segmented entry
postingList = [
	['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
	['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
	['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
	['stop', 'posting', 'stupid', 'worthless', 'garbage'],
	['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
	['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
]
# Category label vector, 1 for insulting words, 0 for not
classVec = [0, 1, 0, 1, 0, 1]

2.2 data processing steps

If we want to judge whether it is an insulting word group, we need to calculate the probability that each word in a group of words is an insulting word through the basic judgment data, and then add up the same word probability in the group to get the insulting probability and non insulting probability. After the basic probability is obtained, the final judgment can be obtained by calculating the word group to be judged.

1. Count all words (de duplication)
2. Copy the total number, compare the total data with each phrase, and get the corresponding total number of data Vectorization
3. According to the classification of word groups, the total data of vectorization is used to get the insulting probability and non insulting probability of each word
4. Then we use probability to classify test word groups

However, if we just do this, we will find that the insulting probability and non insulting probability either have a value or are 0. In the subsequent processing, the probability will be 0 because the value is too small according to the conditional probability formula, and the classification will be wrong.

So we need to improve Laplace smoothing by naive Bayes

2.3. Complete code

# !/usr/bin/python
# -*- coding: utf-8 -*- 
# @Time : 2020/1/1 22:48 
# @Author : ljf
# @File : NB_test6.py
import numpy as np


def loadDataSet():
    """
    //Function Description: create experiment sample
    Returns:
        postingList:    Experimental sample segmentation terms
        classVec:       Category label vector
    """
    # Segmented entry
    postingList = [
        ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
        ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
        ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
        ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
        ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
        ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
    ]
    classVec = [0, 1, 0, 1, 0, 1]  # Category label vector, 1 for insulting words, 0 for not
    return postingList, classVec


def setOfWords2Vec(vocabList, inputSet):
    """
    //Function Description: quantize the inputSet according to the vocabList vocabulary, and each element of the vector is 1 or 0
    Args:
        vocabList:  createVocabList List returned
        inputSet:   List of segmented entries
    Returns:
        returnVec:  Document vector,Word set model
    """
    returnVec = [0] * len(vocabList)  # Create a vector in which all elements are 0
    for word in inputSet:  # Traverse each entry
        if word in vocabList:  # Set 1 if entry exists in Glossary
            returnVec[vocabList.index(word)] = 1
        else:
            print("the word: %s is not in my Vocabulary!" % word)
    return returnVec  # Return document vector


def createVocabList(dataSet):
    """
    //Function Description: organize the segmented experimental sample entries into a list of non repeated entries, that is, a glossary
    Args:
        dataSet:    Collated sample data set
    Returns:
        vocabSet:   Returns a list of entries that are not repeated, that is, a glossary
    """
    vocabSet = set([])  # Create an empty non repeating list
    for document in dataSet:
        vocabSet = vocabSet | set(document)  # Union and collection
    return list(vocabSet)


def trainNB0(trainMatrix, trainCategory):
    """
    //Function Description: naive Bayesian classifier training function
    Args:
        trainMatrix:    Training document matrix, i.e setOfWords2Vec Returned returnVec Constructed matrix
        trainCategory:  Training category label vector, i.e loadDataSet Returned classVec
    Returns:
        p0Vect:     Conditional probability array of non insulting class
        p1Vect:     Conditional probability array of insulting class
        pAbusive:   The probability that documents belong to insults
    """
    numTrainDocs = len(trainMatrix)  # Count the number of documents trained
    numWords = len(trainMatrix[0])  # Count entries per document
    pAbusive = sum(trainCategory) / float(numTrainDocs)  # The probability that documents belong to insults
    p0Num = np.zeros(numWords)
    p1Num = np.zeros(numWords)  # Create the numpy.zeros array and initialize the number of entries to 0
    p0Denom = 0.0
    p1Denom = 0.0  # Denominator initialized to 0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:  # Data required for statistics of conditional probabilities belonging to insults, i.e. P(w0|1),P(w1|1),P(w2|1)···
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:  # Data required for statistics of conditional probabilities belonging to non insulting categories, i.e. P(w0|0),P(w1|0),P(w2|0)···
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = p1Num / p1Denom
    p0Vect = p0Num / p0Denom
    return p0Vect, p1Vect, pAbusive  # Returns the conditional probability array belonging to the insulting class, the conditional probability array belonging to the non insulting class, and the probability of the document belonging to the insulting class


def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    """
    //Function Description: naive Bayesian classifier classification function
    Args:
        vec2Classify:   Array of terms to be classified
        p0Vec:          Conditional probability array of insulting class
        p1Vec:          Conditional probability array of non insulting class
        pClass1:        The probability that documents belong to insults
    Returns:
        0:              Non insulting
        1:              It's an insult
    """
    p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)  # The corresponding elements are multiplied. logA * B = logA + logB, so add log(pClass1) here
    p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
    print('p0:', p0)
    print('p1:', p1)
    if p1 > p0:
        return 1
    else:
        return 0


def testingNB():
    """
    //Function Description: Test naive Bayes classifier
    Returns:
        //nothing
    """
    listOPosts, listClasses = loadDataSet()  # Create an experiment sample
    myVocabList = createVocabList(listOPosts)  # Create Glossary
    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))  # Quantify the experimental samples
    p0V, p1V, pAb = trainNB0(np.array(trainMat), np.array(listClasses))  # Training naive Bayesian classifier

    testEntry = ['love', 'my', 'dalmation']  # Test sample 1
    thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))  # Test sample Vectorization
    if classifyNB(thisDoc, p0V, p1V, pAb):
        print(testEntry, 'It's an insult')  # Perform classification and print classification results
    else:
        print(testEntry, 'Non insulting')  # Perform classification and print classification results

    testEntry = ['stupid', 'garbage']  # Test sample 2
    thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))  # Test sample Vectorization
    if classifyNB(thisDoc, p0V, p1V, pAb):
        print(testEntry, 'It's an insult')  # Perform classification and print classification results
    else:
        print(testEntry, 'Non insulting')  # Perform classification and print classification results


if __name__ == '__main__':
    testingNB()

Three, summary

• Before training naive Bayesian classifier, there are still many things to be learned in text cleaning.
• According to the extracted classification features, the text is vectorized, and then naive Bayesian classifier is trained.
• The difference in the number of De high frequency words has an impact on the results.
• Laplacian smoothing plays an active role in improving the classification effect of naive Bayesian classifier.