catalogue
4 quantum genetic algorithm -- Python implementation
5 quantum genetic algorithm -- Matlab implementation
1 important knowledge points
In the column, I have systematically summarized the genetic algorithm: *Intelligent optimization algorithm (continuously updating...) , let's first explain the important knowledge points, and then implement them with Python and Matlab respectively.
1.1 genetic algorithm
Genetic algorithm is an intelligent algorithm that simulates Darwin's theory of biological evolution and genetic variation. This algorithm has the advantages of strong robustness (used to represent the insensitivity of the control system to characteristic or parameter disturbance), standardized implementation steps, simplicity and universality. It is widely used in the fields of artificial intelligence, multi-objective decision-making, society and economy. However, the general genetic algorithm has some limitations: slow convergence speed, many iterations, easy to converge prematurely and easy to fall into the local optimal solution.
1.2 quantum computing
Quantum computing is a comprehensive interdisciplinary subject of quantum mechanics and information science. Quantum computing has the parallelism of quantum mechanics and faster computing speed; At the same time, there are many kinds of quantum states, and they rarely fall into local extremum when searching the optimal solution.
1.3 quantum genetic algorithm
Quantum genetic algorithm introduces the quantum state vector into genetic algorithm, and applies the probability amplitude of quantum bits to chromosome coding. A chromosome is the superposition of multiple quantum states. The quantum revolving gate is used to realize the mutation and renewal of chromosome. Therefore, quantum genetic algorithm has the advantages of less iterations, fast running speed, genetic variation with less population, wide search range and difficult to fall into local extremum.
To learn more about quantum genetic algorithms, you can read the following two articles:
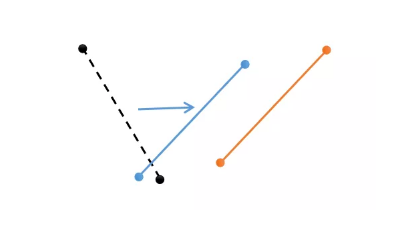
The characteristics of quantum genetic algorithm are briefly introduced through a picture. The Yellow individual has the current optimal value, and the black is some other individual. After one iteration, the black individual will rotate and approach the Yellow individual. The quantum genetic algorithm replaces the original crossover process with a rotating gate. The individual has two function values. The convergence speed of optimization is faster. There is a rotation process to find the optimal. There is also an inertia formula in the rotation formula, that is, the rotation amplitude will decrease with the increase of the number of iterations. Compared with the genetic algorithm as a whole, it is more difficult to fall into the local optimal.
2. Operation steps
2.1 using qubits to initialize parent chromosomes
In traditional binary computing, values are represented by | 0 "and | 1", which are bits. Similarly, in the process of quantum computing, two basic states representing quantum are used, which are called qubits. Various states of qubits are expressed by the following formula:
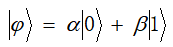
Among them, α And β Is a complex number, which is called probability amplitude, and α And β satisfy
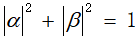
It is equivalent to
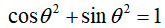
The quantum state can be expressed as:
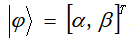
Quantum genetic algorithm expresses the genes on the chromosome with quantum bits, so as to increase the population diversity. m chromosomes are randomly generated, and the genes on each chromosome are represented by quantum bits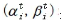
, and initialized to
.
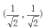2.2 in quantum genetic algorithm, chromosomes are encoded by the probability amplitude of qubits. The coding scheme is as follows:
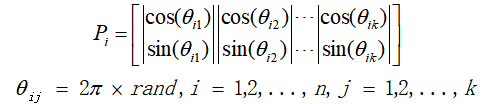
Pi is the ith gene, the phase of qubits, n is the number of chromosomes, k is the number of qubits, that is, the dimension of solution space, and rand is a random number in the range of [0,1]. Each qubit is divided into two lines, corresponding to the probability amplitudes of the two quantum basic states respectively, which meets the normalization condition. Therefore, each individual contains two cultural gene chains, and each gene chain is a candidate solution of the optimization problem. It can be seen that under the condition of constant population size, the number of candidate solutions of quantum genetic algorithm is twice that of genetic algorithm, which increases the diversity of understanding space and improves the probability of successful optimization.
2.3 measure each individual in the initialization population.
Randomly generate a number x ∈ [0,1], if
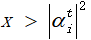
Then the measured value is taken as 1, otherwise it is taken as 0.
2.4 evaluate the fitness of each measured value to select the best individual and carry out genetic variation.
2.5 use quantum revolving gate to update the next generation of individuals. Quantum revolving gate is a commonly used method in logic gate, which is specifically expressed as:
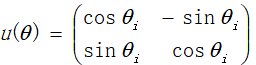
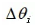Is the angle of quantum rotation, then the update of quantum bit is expressed as:
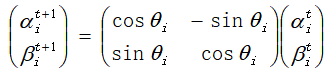
2.6 iteration, y=y+1
The optimal solution is obtained by setting the individual termination condition 2.7.
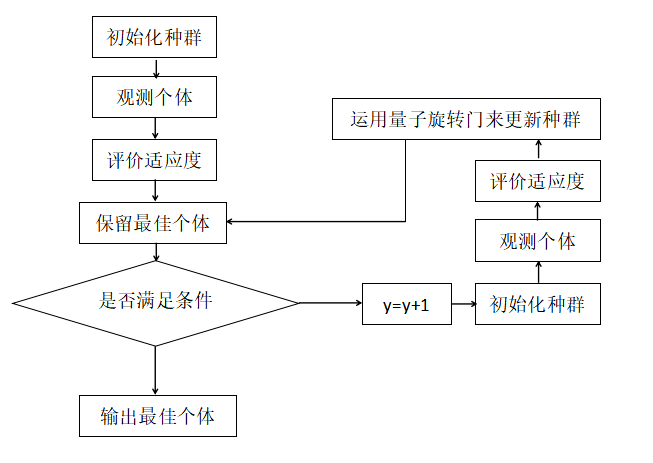
3 flow chart
4 quantum genetic algorithm -- Python implementation
4.1 data
4.2 code
# -*- coding: utf-8 -*-
#==========Import package============
import numpy as np
from sklearn import svm #SVM is a binary classifier
from sklearn import cross_validation #Cross validation is a statistical analysis method used to verify the performance of classifiers
import random
import math
import matplotlib.pyplot as plt
#=======1. Import training data========
def load_data(data_file):
'''
input: data_file(string):File of training data
output: data(mat):Characteristics of training samples
label(mat):Label of training sample
'''
data = []
label = []
f = open(data_file)
for line in f.readlines():
lines = line.strip().split(' ')
#===Extracted label===
label.append(float(lines[0]))
#==Extract features and put them into the matrix===
index = 0
tmp = []
for i in range(1, len(lines)):
li = lines[i].strip().split(":")
if int(li[0]) - 1 == index:
tmp.append(float(li[1]))
else:
while(int(li[0]) - 1 > index):
tmp.append(0)
index += 1
tmp.append(float(li[1]))
index += 1
while len(tmp) < 13:
tmp.append(0)
data.append(tmp)
f.close()
return np.array(data), np.array(label).T
#===============================2. QGA algorithm=================================================
class QGA(object):
#====2.1 class initialization======
'''definition QGA class
'''
def __init__(self,population_size,chromosome_num,chromosome_length,max_value,min_value,iter_num,deta):
'''Initialization class parameters
population_size(int):Population number
chromosome_num(int):Chromosome number, corresponding to the number of parameters to be optimized
chromosome_length(int):Chromosome length
max_value(float):Maximum decimal value of chromosome
min_value(float):Chromosome decimal value minimum
iter_num(int):Number of iterations
deta(float):Quantum rotation angle
'''
self.population_size = population_size
self.chromosome_num = chromosome_num
self.chromosome_length = chromosome_length
self.max_value = max_value
self.min_value = min_value
self.iter_num = iter_num
self.deta = deta
#======2.2 quantum form initialization of population=================
def species_origin_angle(self):
'''Population initialization
input:self(object):QGA class
output:population_Angle(list):Quantum angle list of population
population_Angle2(list):The quantum angle list of empty population is used to store the crossed quantum angle list
'''
population_Angle = []
for i in range(self.chromosome_num):
tmp1 = [] #Store the quantum angles of all values of each chromosome
for j in range(self.population_size):
tmp2 = [] #Storage quantum angle
for m in range(self.chromosome_length):
a = np.pi * 2 * np.random.random()
tmp2.append(a)
tmp1.append(tmp2)
population_Angle.append(tmp1)
return population_Angle
#======Convert the initialized quantum angle sequence into a list of quantum coefficients of the population======
def population_Q(self,population_Angle):
'''
input:self(object):QGA class
population_Angle(list):Quantum angle list of population
output:population_Q(list):List of quantum coefficients of population
'''
population_Q = []
for i in range(len(population_Angle)):
tmp1 = [] #Store the quantum coefficient pairs of all values of each chromosome
for j in range(len(population_Angle[i])):
tmp2 = [] #Storing quantum pairs for each value of each chromosome
tmp3 = [] #Store half of the quantum pair
tmp4 = [] #Storing the other half of a quantum pair
for m in range(len(population_Angle[i][j])):
a = population_Angle[i][j][m]
tmp3.append(np.sin(a))
tmp4.append(np.cos(a))
tmp2.append(tmp3)
tmp2.append(tmp4)
tmp1.append(tmp2)
population_Q.append(tmp1)
return population_Q
#2.3 ==== calculate fitness function value==============
def translation(self,population_Q):
'''Convert the quantum list of population to binary list
input:self(object):QGA class
population_Q(list):Quantum list of populations
output:population_Binary:Binary list of populations
'''
population_Binary = []
for i in range(len(population_Q)):
tmp1 = [] # Store all values of each chromosome in binary form
for j in range(len(population_Q[i])):
tmp2 = [] ##Store the binary form of each value of each chromosome
for l in range(len(population_Q[i][j][0])):
if np.square(population_Q[i][j][0][l]) > np.random.random():
tmp2.append(1)
else:
tmp2.append(0)
tmp1.append(tmp2)
population_Binary.append(tmp1)
return population_Binary
#===Find the numerical list of fitness function. The fitness function used in this experiment is RBF_ 3 of SVM_ Fold cross validation average===
def fitness(self,population_Binary):
'''
input:self(object):QGA class
population_Binary(list):Binary list of populations
output:fitness_value(list):Fitness function value class table
parameters(list):List of corresponding optimization parameters
'''
#===(1) The binary representation of the chromosome is converted to decimal and set between [min_value,max_value]===
parameters = [] #Store the possible values of all parameters
for i in range(len(population_Binary)):
tmp1 = [] #Store the possible values of a parameter
for j in range(len(population_Binary[i])):
total = 0.0
for l in range(len(population_Binary[i][j])):
total += population_Binary[i][j][l] * math.pow(2,l) #Calculate the decimal value corresponding to binary
value = (total * (self.max_value - self.min_value)) / math.pow(2,len(population_Binary[i][j])) + self.min_value ##Place the decimal value between [min_value,max_value]
tmp1.append(value)
parameters.append(tmp1)
#====(2) The fitness function is RBF_ 3 of SVM_ Fold cross check average=========
fitness_value = []
for l in range(len(parameters[0])):
rbf_svm = svm.SVC(kernel = 'rbf', C = parameters[0][l], gamma = parameters[1][l])
cv_scores = cross_validation.cross_val_score(rbf_svm,trainX,trainY,cv =3,scoring = 'accuracy')
fitness_value.append(cv_scores.mean())
#=====(3) Find the optimal fitness function value and the corresponding binary representation of parameters======
best_fitness = 0.0
best_parameter = []
best_parameter_Binary = []
for j in range(len(population_Binary)):
tmp2 = []
best_parameter_Binary.append(tmp2)
best_parameter.append(tmp2)
for i in range(len(population_Binary[0])):
if best_fitness < fitness_value[i]:
best_fitness = fitness_value[i]
for j in range(len(population_Binary)):
best_parameter_Binary[j] = population_Binary[j][i]
best_parameter[j] = parameters[j][i]
return parameters,fitness_value,best_parameter_Binary,best_fitness,best_parameter
#============2.4 full interference crossover===============
def crossover(self,population_Angle):
'''Full interference crossover of population quantum angle list
input:self(object):QGA class
population_Angle(list):Quantum angle list of population
'''
#===Initialize an empty list, the list of quantum angles after full interference crossing==
population_Angle_crossover = []
for i in range(self.chromosome_num):
tmp11 = []
for j in range(self.population_size):
tmp21 = []
for m in range(self.chromosome_length):
tmp21.append(0.0)
tmp11.append(tmp21)
population_Angle_crossover.append(tmp11)
for i in range(len(population_Angle)):
for j in range(len(population_Angle[i])):
for m in range(len(population_Angle[i][j])):
ni = (j - m) % len(population_Angle[i])
population_Angle_crossover[i][j][m] = population_Angle[i][ni][m]
return population_Angle_crossover
#============2.4 variation==================
def mutation(self,population_Angle_crossover,population_Angle,best_parameter_Binary,best_fitness):
'''Quantum mutation using quantum gate transformation matrix
input:self(object):QGA class
population_Angle_crossover(list):List of quantum angles after full interference crossing
output:population_Angle_mutation(list):List of quantum angles after mutation
'''
#==(1) Get the fitness function value list after crossing=======
population_Q_crossover = self.population_Q(population_Angle_crossover) ## List of population quantum coefficients after crossover
population_Binary_crossover = self.translation(population_Q_crossover) ## Binary number list of populations after crossover
parameters,fitness_crossover,best_parameter_Binary_crossover,best_fitness_crossover,best_parameter = self.fitness(population_Binary_crossover) ## List of fitness function values after crossing
#==(2) Initializes the rotation angle of each qubit====
Rotation_Angle = []
for i in range(len(population_Angle_crossover)):
tmp1 = []
for j in range(len(population_Angle_crossover[i])):
tmp2 = []
for m in range(len(population_Angle_crossover[i][j])):
tmp2.append(0.0)
tmp1.append(tmp2)
Rotation_Angle.append(tmp1)
deta = self.deta
#====(3) Find the rotation angle of each qubit========
for i in range(self.chromosome_num):
for j in range(self.population_size):
if fitness_crossover[j] <= best_fitness:
for m in range(self.chromosome_length):
s1 = 0
a1 = population_Q_crossover[i][j][0][m]
b1 = population_Q_crossover[i][j][1][m]
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 0 and a1 * b1 > 0:
s1 = -1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 0 and a1 * b1 < 0:
s1 = 1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 0 and a1 * b1 == 0:
s1 = 1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 1 and a1 * b1 < 0:
s1 = -1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 1 and a1 * b1 == 0:
s1 = 1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 0 and a1 * b1 > 0:
s1 = -1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 0 and a1 * b1 < 0:
s1 = 1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 0 and a1 * b1 == 0:
s1 = -1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 1 and a1 * b1 > 0:
s1 = 1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 1 and a1 * b1 < 0:
s1 = -1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 1 and a1 * b1 == 0:
s1 = 1
Rotation_Angle[i][j][m] = deta * s1
else:
for m in range(self.chromosome_length):
s2 = 0
a2 = population_Q_crossover[i][j][0][m]
b2 = population_Q_crossover[i][j][1][m]
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 0 and a2 * b2 > 0:
s2 = -1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 0 and a2 * b2 < 0:
s2 = 1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 0 and a2 * b2 == 0:
s2 = 1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 1 and a2 * b2 > 0:
s2 = -1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 1 and a2 * b2 < 0:
s2 = 1
if population_Binary_crossover[i][j][m] == 0 and best_parameter_Binary[i][m] == 1 and a2 * b2 == 0:
s2 = 1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 0 and a2 * b2 > 0:
s2 = 1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 0 and a2 * b2 < 0:
s2 = -1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 0 and a2 * b2 == 0:
s2 = 1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 1 and a2 * b2 > 0:
s2 = 1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 1 and a2 * b2 < 0:
s2 = -1
if population_Binary_crossover[i][j][m] == 1 and best_parameter_Binary[i][m] == 1 and a2 * b2 == 0:
s2 = 1
Rotation_Angle[i][j][m] = deta * s2
#=======(4) According to the rotation angle of each qubit, a new list of quantum angles of the population is generated===============
for i in range(self.chromosome_num):
for j in range(self.population_size):
for m in range(self.chromosome_length):
population_Angle[i][j][m] = population_Angle[i][j][m] + Rotation_Angle[i][j][m]
return population_Angle
#======2.5 draw the change diagram of fitness function value======
def plot(self,results):
'''
Draw a picture
'''
X = []
Y = []
for i in range(self.iter_num):
X.append(i + 1)
Y.append(results[i])
plt.plot(X,Y)
plt.xlabel('Number of iteration',size = 15)
plt.ylabel('Value of CV',size = 15)
plt.title('QGA_RBF_SVM parameter optimization')
plt.show()
#===========2.6 main function================
def main(self):
results = []
best_fitness = 0.0
best_parameter = []
#===Population initialization===
population_Angle= self.species_origin_angle()
#===Iteration====
for i in range(self.iter_num):
population_Q = self.population_Q(population_Angle)
## Calculate the fitness function value list of this iteration, the optimal fitness function value and the corresponding parameters
parameters,fitness_value,current_parameter_Binary,current_fitness,current_parameter = self.fitness(population_Binary)
## Find out the best fitness function value and corresponding parameters so far
if current_fitness > best_fitness:
best_fitness = current_fitness
best_parameter = current_parameter
print('iteration is :',i+1,';Best parameters:',best_parameter,';Best fitness',best_fitness)
results.append(best_fitness)
## Total interference crossover
population_Angle_crossover = self.crossover(population_Angle)
## Quantum rotation variation
population_Angle = self.mutation(population_Angle_crossover,population_Angle,current_parameter_Binary,current_fitness)
if __name__ == '__main__':
print('----------------1.Load Data-------------------')
trainX,trainY = load_data('rbf_data')
print('----------------2.Parameter Seting------------')
population_size=200
chromosome_num=2
chromosome_length=20
max_value=15
min_value=0.01
iter_num=100
deta=0.1 * np.pi
print('----------------3.QGA_RBF_SVM-----------------')
qga = QGA(population_size,chromosome_num,chromosome_length,max_value,min_value,iter_num,deta)
qga.main()
4.3 results
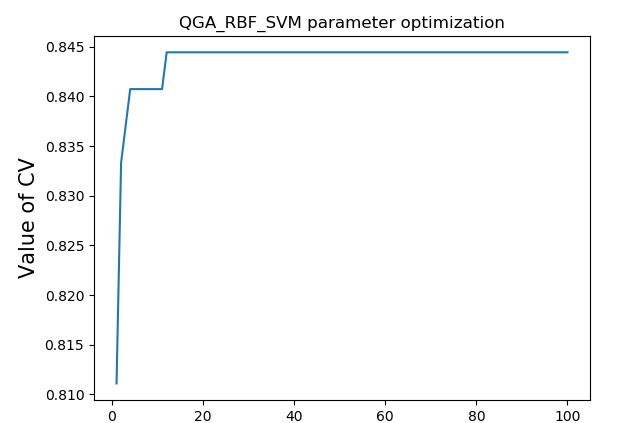
5 quantum genetic algorithm -- Matlab implementation
clear,clc
%% 1 Basic concepts
%(1)Quantum genetic algorithm is an intelligent optimization algorithm combining quantum computing and genetic algorithm K.H.Han They introduced quantum concepts such as quantum state, quantum gate, quantum state characteristics and probability amplitude into genetic algorithm.
%Quantum genetic algorithm is also a probabilistic prime search algorithm, which uses qubits to represent genes. The gene of genetic algorithm expresses certain information, while in quantum genetic algorithm, the gene expressed by qubit contains all possible information due to the superposition of quantum information.
%(2)In quantum computing, qubits｜0〉and｜1〉It represents two basic states of micro particles. According to the superposition principle, the superposition state of quantum information can be expressed as a linear combination of these two basic states, i.e｜ψ〉=α｜0〉+β｜1〉，WhereαandβIs a complex number, which represents the probability amplitude of the qubit state, where and represent the quantum state respectively｜ψ〉Collapse due to measurement to｜0〉State sum｜1〉The probability of the state and satisfies the normalization condition
%(3)In quantum genetic algorithm, chromosomes are encoded by the probability amplitude of qubits. The coding scheme is as follows:
%θIs the phase of the qubit, n Is the number of chromosomes, k Is the number of qubits, that is, the dimension of the solution space, rand yes[0,1]Random number in the range. Each qubit is divided into two lines, corresponding to the probability amplitudes of the two quantum basic states respectively, which meets the normalization condition. Therefore, each individual contains two cultural gene chains, and each gene chain is a candidate solution of the optimization problem. It can be seen that under the condition of constant population size, the number of candidate solutions of quantum genetic algorithm is twice that of genetic algorithm, which increases the diversity of understanding space and improves the probability of successful optimization.
%(4)In quantum genetic algorithm, quantum revolving gate is used to change the phase of qubit to update the probability amplitude of qubit, so as to achieve the effect of gene mutation.
%% 2,Basic steps of quantum genetic algorithm:
%step1: Initialize parent chromosome
%step2: The quantile of each chromosome is measured to get a state. Calculate the fitness for each state and record the best individual and fitness.
%step3: The algebra set by genetic evolution, in which the quantum revolving gate is used to carry out genetic variation on the chromosomes of each generation.
%step4: When the termination condition is reached, the best individual and fitness are output.
%% 3,Quantum genetic algorithm MATLAB The implementation code is as follows
%% Variable part
popsize = 100; %Population size
vartotal = 2; %The number of variables is the quantum number of a chromosome
shiftstep = 0.01*pi; %Corner step
Pm = ones(1,popsize)*0.05;%Set mutation probability
maxgen = 200; %Set the number of iterations
%% Array part--Value range of optimization variables in solution space
var_range(1,1) = -100;
var_range(1,2) = 100;
var_range(2,1) = -100;
var_range(2,2) = 100;
%% Individual initialization
%Initialized 2*popsize Individuals, each of which has two gene chains
for i=1:1:vartotal
fai(:,i)=2*pi*rand(popsize,1);
chrom(:,1,i)=cos(fai(:,i));
chrom(:,2,i)=sin(fai(:,i));
oldfai(:,i)=2*pi*rand(popsize,1);
oldchrom(:,1,i)=cos(oldfai(:,i));
oldchrom(:,2,i)=sin(oldfai(:,i));
end
%% Solution space transformation
for i=1:1:2
for j=1:1:vartotal
chromx(:,i,j)=0.5*(var_range(j,2)*(1+chrom(:,i,j))+var_range(j,1)*(1-chrom(:,i,j)));
oldchromx(:,i,j)=0.5*(var_range(j,2)*(1+oldchrom(:,i,j))+var_range(j,1)*(1-oldchrom(:,i,j)));
end
end
%% Calculate fitness---Fitness function: Shaffer's F6 function
for i=1:1:popsize
for j=1:1:2
x1=chromx(i,j,1);
x2=chromx(i,j,2);
fitness(i,j)=0.5-((sin(sqrt(x1^2+x2^2)))^2-0.5)/(1+0.001*(x1^2+x2^2))^2;
x1=oldchromx(i,j,1);
x2=oldchromx(i,j,2);
oldfitness(i,j)=0.5-((sin(sqrt(x1^2+x2^2)))^2-0.5)/(1+0.001*(x1^2+x2^2))^2;
end
end
%% Obtain the optimal solution and corresponding independent variables
[Bestf,Indexf]=sort(fitness,2);
[BestF,IndexF]=sort(Bestf,1);
gBestfit=BestF(popsize,2);
gBestpop=IndexF(popsize,2);
gBestg=Indexf(gBestpop,2);
gBestfai=fai(gBestpop,:);
gBestC=chrom(gBestpop,:,:);
gBest_x=chromx(gBestpop,:,:);
gBest_fit=fitness(gBestpop,:);
%% Start of main cycle
for gen = 1:1:maxgen
for i = 1:1:vartotal
tmp=abs(chromx(1,gBestg,i)-oldchromx(1,gBestg,i));
if tmp<1.0e-2
tmp=1.0e-2;
end
max(i)=abs(fitness(1,gBestg)-oldfitness(1,gBestg))/tmp;
min(i)=abs(fitness(1,gBestg)-oldfitness(1,gBestg))/tmp;
for j = 1:1:popsize
tmp=abs(chromx(j,gBestg,i)-oldchromx(j,gBestg,i));
if tmp<1.0e-2
tmp=1.0e-2;
end
if max(i)<=abs(fitness(j,gBestg)-oldfitness(j,gBestg))/tmp
max(i)=abs(fitness(j,gBestg)-oldfitness(j,gBestg))/tmp;
end
if min(i)>abs(fitness(j,gBestg)-oldfitness(j,gBestg))/tmp
min(i)=abs(fitness(j,gBestg)-oldfitness(j,gBestg))/tmp;
end
end
end
%% Perform qubit phase rotation to obtain a new phase
for i=1:1:popsize
for j = 1:1:vartotal
tmp=abs(chromx(i,gBestg,j)-oldchromx(i,gBestg,j));
if tmp<1.0e-2
tmp=1.0e-2;
end
grad=abs(fitness(i,gBestg)-oldfitness(i,gBestg))/tmp;
tmp=abs(grad-min(j));
if tmp<1.0e-2
tmp=1.0e-2;
end
rate(i,j)=tmp/abs(max(j)-min(j));
if max(j)-min(j)==0
rate(i,j)=1;
end
fai(i,j)=fai(i,j)+sign(chrom(i,1,j)*gBestC(1,2,j)-gBestC(1,1,j)*chrom(i,2,j))*(1-rate(i,j))*shiftstep*exp(-gen/maxgen);
end
end
%% Execute qubit phase variation
Pm_rand = rand(popsize,vartotal);%Generate a random number and compare it with the mutation probability to determine whether to mutate
for i=1:1:popsize
for j=1:1:vartotal
if (Pm(i)>Pm_rand(i,j))&&(i==gBestpop)
fai(i,j)=0.5*pi-fai(i,j);
end
end
end
%% Intergenerational replication---Two adjacent generations are preserved
oldchrom=chrom;
oldchromx=chromx;
oldfitness=fitness;
%% Generate new quantum individuals
chrom(:,1,:)=cos(fai(:,:));
chrom(:,2,:)=sin(fai(:,:));
%% Solution space transformation
for i=1:1:2
for j=1:1:vartotal
chromx(:,i,j)=0.5*(var_range(j,2)*(1+chrom(:,i,j))+var_range(j,1)*(1-chrom(:,i,j)));
end
end
%% Calculate fitness---Fitness function: Shaffer's F6 function
for i=1:1:popsize
for j=1:1:2
x1=chromx(i,j,1);
x2=chromx(i,j,2);
fitness(i,j)=0.5-((sin(sqrt(x1^2+x2^2)))^2-0.5)/(1+0.001*(x1^2+x2^2))^2;
end
end
%% Obtain the optimal solution and corresponding independent variables
[Bestf,Indexf]=sort(fitness,2);
[BestF,IndexF]=sort(Bestf,1);
Bestfit=BestF(popsize,2);
Bestpop=IndexF(popsize,2);
Bestg=Indexf(Bestpop,2);
Bestfai=fai(Bestpop,:);
BestC=chrom(Bestpop,:,:);
Best_x=chromx(Bestpop,:,:);
Best_fit=fitness(Bestpop,:);
Badpop=IndexF(1,1);
%% If the optimal solution degenerates, the previous generation optimal solution is retrieved
if Bestfit<gBestfit
Bestfit=gBestfit;
fai(Badpop,:)=gBestfai(1,:);
chrom(Badpop,:,:)=gBestC(1,:,:);
chromx(Badpop,:,:)=gBest_x(1,:,:);
fitness(Badpop,:)=gBest_fit(1,:);
gBestpop=Badpop;%The worst chromosome number becomes the best
end
%% If the optimal solution evolves, the optimal solution is replaced
if Bestfit>=gBestfit
gBestfit=Bestfit;
gBestpop=Bestpop;
gBestg=Bestg;
gBestfai=Bestfai;
gBestC=BestC;
gBest_x=Best_x;
gBest_fit=Best_fit;
end
%---------------------Record optimization results---------------------
result(gen)=gBestfit;
end
%% End of main cycle
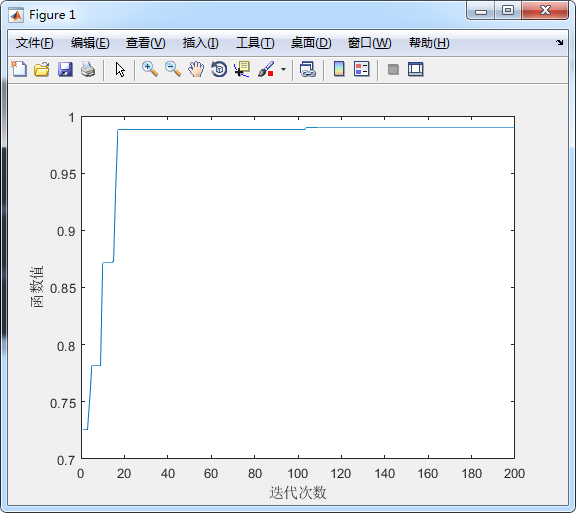
bestresult=result(gen)
figure(1)
plot(1:maxgen,result)
xlabel('Number of iterations')
ylabel('function value')
