Many algorithms or interview questions will involve the problem of dynamic programming. From a mathematical point of view, dynamic programming has a problem
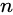
A collection of elements
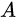
. This collection can build
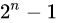
Two combined set classes:
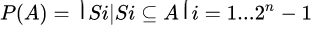
The solution of the problem is to find the subset that meets the conditions
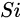
Come on. Conversely, we can traverse each subset in the set class, and then judge whether this subset meets the problem conditions. If so, we can process the subset, and finally get the optimal solution. The time complexity of this method is
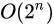
, although not the best solution, it is the most common solution to violence.
The general solution can be realized according to the above rules according to the following steps (this paper is implemented in OC language, and other languages can refer to):
1. Traverse all subsets in the set class
The traversal of subsets can be realized by recursive method. The code is as follows:
/**
array:Specifies the collection to process
start:The position of the first element
subArray: Save the subset obtained by traversal.
*/
void dynamicProgram(NSArray *array, NSInteger start, NSMutableArray *subArray) {
//Recursive calls generate subsets in the set class respectively.
NSInteger count = array.count;
for (NSInteger i = start; i < count; i++) {
[subArray addObject:array[i]];
//subArray here is a subset of the set class.
//Make recursive calls
dynamicProgram(array, i + 1, subArray);
[subArray removeLastObject];
}
//Examples of methods called are as follows:
dynamicProgram(@[@1,@2,@3,@4], 0, [@[] mutableCopy]);2. Condition judgment and processing for each subset
The above code generates a general method of traversing subsets. In order to make the code more general, we can add a conditional filter and processor respectively to let the caller do custom processing. At the same time, in order to save the results of each processing, we can add a custom context information to save the extension parameters. Therefore, the above code is improved as follows:
//Auxiliary functions.
static void dynamicProgramHelper(NSArray *array, void *ctx, NSInteger start, NSMutableArray *subArray, NSInteger * subIndexs, BOOL(^filter)(NSArray *subArray, NSInteger *subIndexs, void *ctx), BOOL(^handler)(NSArray *subArray, void* ctx) ) {
//Recursive calls generate subsets in the set class respectively.
NSInteger count = array.count;
NSInteger subCount = subArray.count;
for (NSInteger i = start; i < count; i++) {
//Saves the index of the elements in the subset in the collection.
subIndexs[subCount] = i;
[subArray addObject:array[i]];
if (filter(subArray, subIndexs, ctx)) {
if (!handler(subArray,ctx)) {
break;
}
}
dynamicProgramHelper(array, ctx, i + 1, subArray, subIndexs, filter, handler);
[subArray removeLastObject];
}
}
/**
array:Specifies the collection to process
ctx: Save context information
filter: Specify the condition filter. The input parameters are: subset, index array of subset elements in the whole set, and context. If the conditions are met, return true, indicating that calculation processing will be performed; otherwise, return false
handler: Specify the processor. The input parameters are: subset and context. If the best result has been obtained, return false to terminate the processing, otherwise return true to continue the processing.
*/
void dynamicProgram(NSArray *array, void *ctx, BOOL(^filter)(NSArray *subArray, NSInteger *subIndexs, void *ctx), BOOL(^handler)(NSArray *subArray, void *ctx) ) {
NSMutableArray *subArray = [NSMutableArray new];
NSInteger *subIndexs = malloc(sizeof(NSInteger)*array.count);
dynamicProgramHelper(array, ctx, 0, subArray, subIndexs, filter, handler);
free(subIndexs);
}In the above general algorithm, we decompose the processing of dynamic programming into conditions and calculations. The conditions are used to judge whether the calculation requirements are met, and the calculation calculates each subset that meets the conditions. Therefore, if all problems can be divided into conditions and calculations, the problem will be solved. Next, we will use the above general dynamic programming algorithm to solve several classic problems:
1. Thief problem

By analyzing this problem, we can see that the condition is that the houses cannot be adjacent, that is, the index value cannot differ by 1. Calculation is to find the maximum amount. Therefore, the implementation code is as follows:
//Save the maximum amount as a context parameter.
NSInteger maxSum = 0;
dynamicProgram(@[@2,@7,@9,@3,@1], &maxSum, ^BOOL(NSArray *subArray, NSInteger *subIndexs, void *ctx) {
//The condition is that houses cannot be adjacent, so the judgment method is that the indexes of subarrays cannot be connected.
//The algorithm is: if the difference between two indexes is 1, it indicates that the condition is not satisfied.
NSInteger index = subIndexs[0];
for (NSInteger i = 1; i < subArray.count; i++) {
if (index == subIndexs[i] - 1) {
return NO;
}
index = subIndexs[i];
}
return YES;
}, ^BOOL(NSArray *subArray, void *ctx) {
//Calculate the sum of the amounts of the current subset
NSInteger sum = 0;
for (NSNumber *num in subArray) {
sum += num.integerValue;
}
//Judge whether it is the maximum value. If not, modify the maximum value
NSInteger *pmaxSum = (NSInteger*)ctx;
if (sum > *pmaxSum) {
*pmaxSum = sum;
}
return YES;
});
NSLog(@"The biggest amount stolen is:%ld",maxSum);2. Maximum subsequence sum
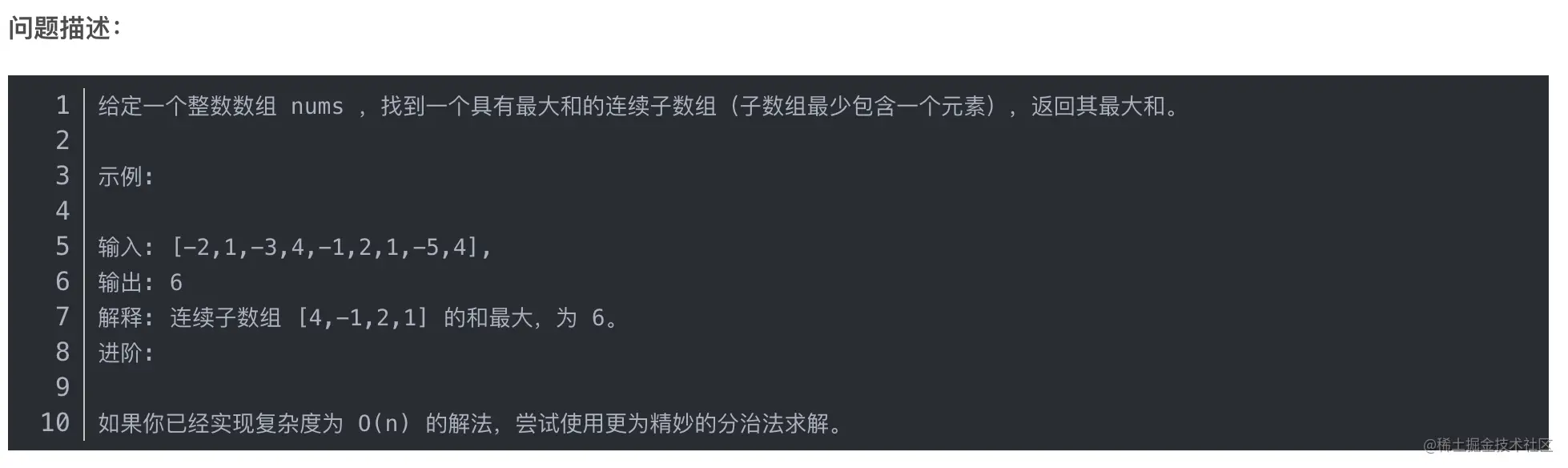
By analyzing this problem, we can see that the condition is that the positions should be adjacent, that is, the index values must differ by 1. Calculation is to find the maximum value. It can be seen that this problem is that the above thief problem has the opposite conditions and the same calculation. Therefore, the implementation code is as follows:
NSInteger maxSum = 0;
dynamicProgram(@[@-2,@1,@-3,@4,@-1,@2,@1,@-5,@4], &maxSum, ^BOOL(NSArray *subArray, NSInteger *subIndexs, void *ctx) {
//The condition is that the positions must be adjacent, so the judgment method is that the indexes of the subarray are adjacent.
//The algorithm is: if there is no difference of 1 between the two indexes, it indicates that the condition is not satisfied.
NSInteger index = subIndexs[0];
for (NSInteger i = 1; i < subArray.count; i++) {
if (index != subIndexs[i] - 1) {
return NO;
}
index = subIndexs[i];
}
return YES;
}, ^BOOL(NSArray *subArray, void *ctx) {
//Calculates the sum of the current subset
NSInteger sum = 0;
for (NSNumber *num in subArray) {
sum += num.integerValue;
}
//Judge whether it is the maximum value. If not, modify the maximum value
NSInteger *pmaxSum = (NSInteger*)ctx;
if (sum > *pmaxSum) {
*pmaxSum = sum;
}
return YES;
});
NSLog(@"Sum of maximal subsequences:%ld",maxSum);3. Coin combination problem
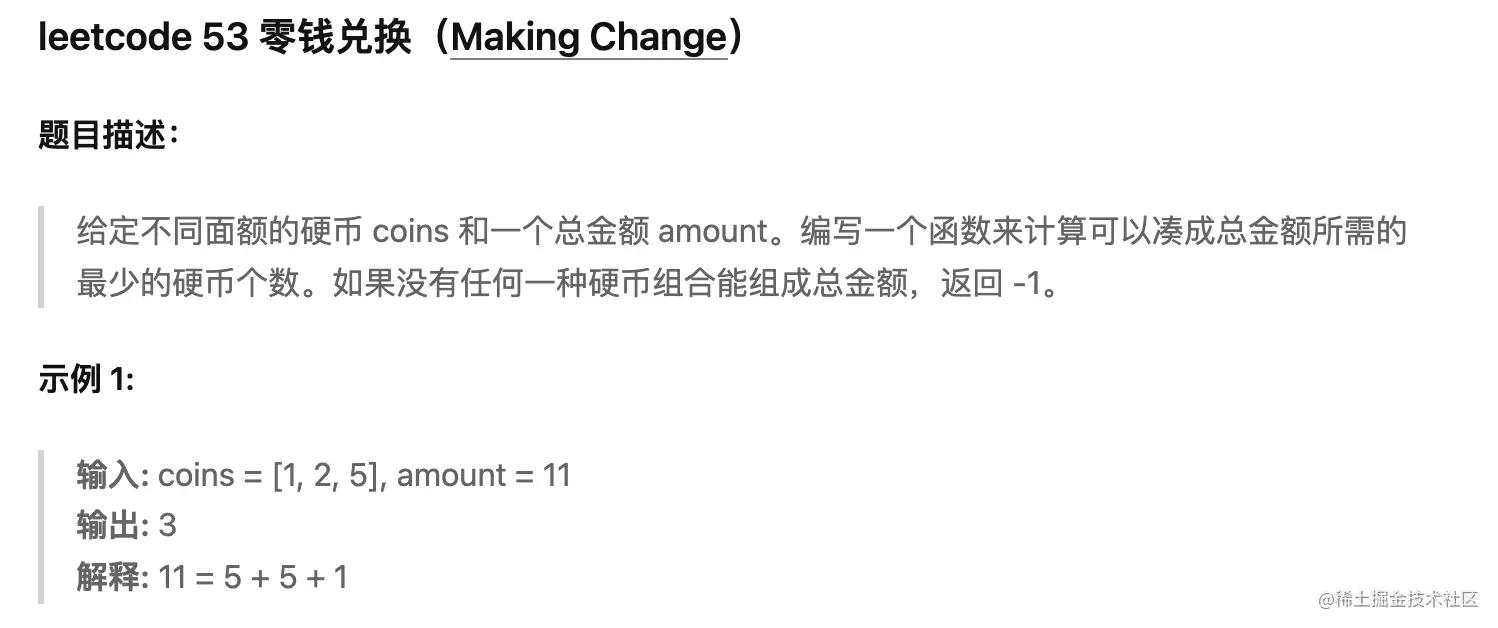
In this problem, if the type of coin is 1, 2, 5, then the total amount is 11 yuan. Therefore, the array should be: [1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,5,5]. The condition becomes that the sum of the amount quantity of the subset must be equal to 11. The calculation is to get the minimum number of subsets. So the code is as follows:
NSArray *coins = @[@1,@1,@1,@1,@1,@1,@1,@1,@1,@1,@1,@2,@2,@2,@2,@2,@5,@5];
//The minimum number at the beginning is the complete set.
NSMutableArray *minCoins = [coins mutableCopy];
dynamicProgram(coins, (__bridge void *)(minCoins), ^BOOL(NSArray *subArray, NSInteger *subIndexs, void *ctx) {
//The condition is that the sum of elements must be equal to 11 yuan.
NSInteger sum = 0;
for (NSNumber *num in subArray) {
sum += num.integerValue;
}
return sum == 11;
}, ^BOOL(NSArray *subArray, void *ctx) {
//Compare the quantity and take the minimum quantity.
NSMutableArray *minCoins = (__bridge NSMutableArray *)(ctx);
if (minCoins.count > subArray.count) {
[minCoins setArray:subArray];
}
return YES;
});