1. Mathematical operations of decimal fixed-point and floating-point numbers
The decimal module implements fixed-point and floating-point arithmetic operations using a model that is familiar to most people, not to programmers (that is, IEEE floating-point arithmetic implemented by most computer hardware).Decimal instances can accurately represent how many numbers are, rounding them off, and limiting the number of valid numbers.
1.1 Decimal
The decimal value is represented as an instance of the Decimal class.The constructor takes an integer or string as a parameter.Before using floating-point numbers to create a Decimal, you can convert the floating-point number to a string so that the caller can explicitly handle the number of bits in the value, because a hardware floating-point representation may not be accurate.Alternatively, the class method from_float() can convert floating-point numbers to exact decimal representations.
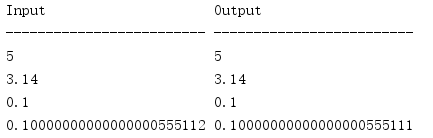
import decimal fmt = '{0:<25} {1:<25}' print(fmt.format('Input', 'Output')) print(fmt.format('-' * 25, '-' * 25)) # Integer print(fmt.format(5, decimal.Decimal(5))) # String print(fmt.format('3.14', decimal.Decimal('3.14'))) # Float f = 0.1 print(fmt.format(repr(f), decimal.Decimal(str(f)))) print('{:<0.23g} {:<25}'.format( f, str(decimal.Decimal.from_float(f))[:25]) )
Floating point value 0.1 is not represented as an exact binary value, so float is not represented as a Decimal value.In the last line of this output, the full string representation is truncated to 25 characters.
Decimal can also be created from tuples containing a symbol symbol symbol (0 for positive and 1 for negative), a tuple of digits, and an integer index.(
import decimal # Tuple t = (1, (1, 1), -2) print('Input :', t) print('Decimal:', decimal.Decimal(t))
Tuple-based representations are not easy to create, but they provide a portable way to export decimal values without losing precision.Tuples can be transported over the network or stored in databases that do not support precise decimal values and then converted back to Decimal instances.
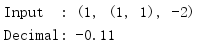
1.2 Formatting
Decimal corresponds to Python's string formatting protocol, using the same syntax and options as other numeric types.(
import decimal d = decimal.Decimal(1.1) print('Precision:') print('{:.1}'.format(d)) print('{:.2}'.format(d)) print('{:.3}'.format(d)) print('{:.18}'.format(d)) print('\nWidth and precision combined:') print('{:5.1f} {:5.1g}'.format(d, d)) print('{:5.2f} {:5.2g}'.format(d, d)) print('{:5.2f} {:5.2g}'.format(d, d)) print('\nZero padding:') print('{:05.1}'.format(d)) print('{:05.2}'.format(d)) print('{:05.3}'.format(d))
The format string controls the width, precision (that is, the number of significant digits) of the output, and the way its fill values occupy the width.

1.3 Arithmetic operations
Decimal overloads simple arithmetic operators, so you can handle Decimal instances in the same way as built-in numeric types.
import decimal a = decimal.Decimal('5.1') b = decimal.Decimal('3.14') c = 4 d = 3.14 print('a =', repr(a)) print('b =', repr(b)) print('c =', repr(c)) print('d =', repr(d)) print() print('a + b =', a + b) print('a - b =', a - b) print('a * b =', a * b) print('a / b =', a / b) print() print('a + c =', a + c) print('a - c =', a - c) print('a * c =', a * c) print('a / c =', a / c) print() print('a + d =', end=' ') try: print(a + d) except TypeError as e: print(e)
Decimal operators also accept integer parameters, but floating-point values must be converted to Decimal instances before they can be used.

In addition to basic arithmetic operations, Decimal also includes methods for finding base-10 logarithms and natural logarithms.The values returned by log10() and ln() are Decimal instances, so they can be used directly in the formula like other values.
1.4 Special Value
In addition to the expected numeric values, Decimal can represent many special values, including positive and negative infinity, Not a Number (NaN), and 0.
import decimal for value in ['Infinity', 'NaN', '0']: print(decimal.Decimal(value), decimal.Decimal('-' + value)) print() # Math with infinity print('Infinity + 1:', (decimal.Decimal('Infinity') + 1)) print('-Infinity + 1:', (decimal.Decimal('-Infinity') + 1)) # Print comparing NaN print(decimal.Decimal('NaN') == decimal.Decimal('Infinity')) print(decimal.Decimal('NaN') != decimal.Decimal(1))
Adding to an infinite value returns another infinite value.Comparing equality with NaN always returns false, while comparing inequality always returns true.Comparing the size with NaN to determine the sort order is undefined, which results in an error.

1.5 Context
So far, all previous examples have used the default behavior of the decimal module.You can also use a context to override certain settings, such as maintaining accuracy, how to complete rounding, error handling, and so on.Context can be applied to all Decimal instances in a thread or locally in a small code area.
1.5.1 Current Context
To get the current global context, you can use getcontext().
import decimal context = decimal.getcontext() print('Emax =', context.Emax) print('Emin =', context.Emin) print('capitals =', context.capitals) print('prec =', context.prec) print('rounding =', context.rounding) print('flags =') for f, v in context.flags.items(): print(' {}: {}'.format(f, v)) print('traps =') for t, v in context.traps.items(): print(' {}: {}'.format(t, v))
This sample script shows the common properties of the Context.

1.5.2 Precision
The prec property of the context controls the precision to be maintained for new values created as arithmetic results.Literal values maintain accuracy by this attribute.(
import decimal d = decimal.Decimal('0.123456') for i in range(1, 5): decimal.getcontext().prec = i print(i, ':', d, d * 1)
To change the precision, you can assign a new value directly between 1 and decimal.MAX_PREC for this attribute.

1.5.3 rounding
Rounding has several options to ensure that the values are within the required accuracy range.
ROUND_CEILING: Always rounds up towards infinity.
ROUND_DOWN: Always tends to zero rounding.
ROUND_FLOOR: Always rounds down toward negative infinity.
ROUND_HALF_DOWN: If the last valid number is greater than or greater than 5, it is rounded in the opposite direction of 0; responsible, it is rounded in the direction of 0.
ROUND_HALF_EVEN: Similar to ROUND_HALF_DOWN, however, if the last valid number is 5, the previous digit is checked.Even values cause the result to be rounded down, while odd values cause the result to be rounded up.
ROUND_HALF_UP: Similar to ROUND_HALF_DOWN, but if the last significant number is 5, the value is rounded in the opposite direction of 0.
ROUND_UP: Rounds in the opposite direction of 0.
ROUND_05UP: If the last bit is 0 or 5, it is rounded in the opposite direction of 0; otherwise, it is rounded to 0.
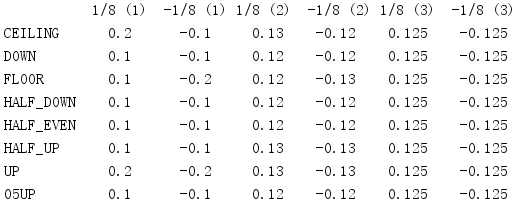
import decimal context = decimal.getcontext() ROUNDING_MODES = [ 'ROUND_CEILING', 'ROUND_DOWN', 'ROUND_FLOOR', 'ROUND_HALF_DOWN', 'ROUND_HALF_EVEN', 'ROUND_HALF_UP', 'ROUND_UP', 'ROUND_05UP', ] header_fmt = '{:10} ' + ' '.join(['{:^8}'] * 6) print(header_fmt.format( ' ', '1/8 (1)', '-1/8 (1)', '1/8 (2)', '-1/8 (2)', '1/8 (3)', '-1/8 (3)', )) for rounding_mode in ROUNDING_MODES: print('{0:10}'.format(rounding_mode.partition('_')[-1]), end=' ') for precision in [1, 2, 3]: context.prec = precision context.rounding = getattr(decimal, rounding_mode) value = decimal.Decimal(1) / decimal.Decimal(8) print('{0:^8}'.format(value), end=' ') value = decimal.Decimal(-1) / decimal.Decimal(8) print('{0:^8}'.format(value), end=' ') print()
This program shows the effect of using different algorithms to round the same value into different precision.
1.5.4 Local Context
You can use the with statement to apply a context to a block of code.
import decimal with decimal.localcontext() as c: c.prec = 2 print('Local precision:', c.prec) print('3.14 / 3 =', (decimal.Decimal('3.14') / 3)) print() print('Default precision:', decimal.getcontext().prec) print('3.14 / 3 =', (decimal.Decimal('3.14') / 3))
Context supports the context manager API used by with, so this setting is only applied within a block.

1.5.5 Context for each instance
You can also construct a Decimal instance with a context from which precision and rounding parameters of the transformation can be inherited.
import decimal # Set up a context with limited precision c = decimal.getcontext().copy() c.prec = 3 # Create our constant pi = c.create_decimal('3.1415') # The constant value is rounded off print('PI :', pi) # The result of using the constant uses the global context print('RESULT:', decimal.Decimal('2.01') * pi)
For example, this allows applications to select common value accuracy that differs from user data accuracy.

1.5.6 Threads
The Global context instance is the thread local context, so you can configure threads individually using different values.
import decimal import threading from queue import PriorityQueue class Multiplier(threading.Thread): def __init__(self, a, b, prec, q): self.a = a self.b = b self.prec = prec self.q = q threading.Thread.__init__(self) def run(self): c = decimal.getcontext().copy() c.prec = self.prec decimal.setcontext(c) self.q.put((self.prec, a * b)) a = decimal.Decimal('3.14') b = decimal.Decimal('1.234') # A PriorityQueue will return values sorted by precision, # no matter what order the threads finish. q = PriorityQueue() threads = [Multiplier(a, b, i, q) for i in range(1, 6)] for t in threads: t.start() for t in threads: t.join() for i in range(5): prec, value = q.get() print('{} {}'.format(prec, value))
This example uses the specified value to create a new context and install it on each thread.
