mathematical problem
Example: the number you can't buy
Xiao Ming opened a candy store.
He is ingenious: wrap the fruit candy into two kinds: a bag of 4 and a bag of 7.
Candy can't be unpacked.
When a child comes to buy sugar, he uses these two kinds of packaging to combine.
Of course, some candies cannot be combined, such as buying 10 candies.
You can test it with a computer. In this case, the maximum quantity you can't buy is 17.
Any number greater than 17 can be combined with 4 and 7.
The requirement of this question is to find the maximum number that cannot be combined when the quantity of two packages is known.
Input format
Two positive integers n,m, indicating the number of sugars in each package.
Output format
A positive integer indicating the maximum number of sugar that cannot be bought.
Data range
2≤n,m≤1000,
Ensure that the data must have a solution.
Input sample:
4 7
Output example:
17
Problem solving ideas


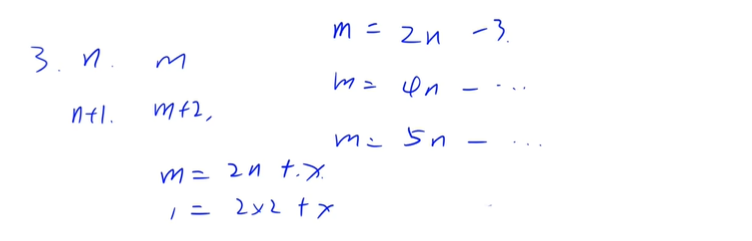
Problem solving code
Violent search
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
bool dfs(int m,int p,int q)
{
if(!m) return true;
if(m>=p&&dfs(m-p,p,q)) return true;
if(m>=q&&dfs(m-q,p,q)) return true;
return false;
}
int main()
{
/***Violent solution***/
int p,q;
cin>>p>>q;
int res =0;
for(int i=1;i<=1000;i++)//enumeration
{
//Find the maximum number that cannot be rounded up
if(!dfs(i,p,q)) res=i;
}
cout <<res<<endl;
return 0;
}Formula solution
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
int main()
{
int p,q;
cin>>p>>q;
cout<<(p-1)*(q-1)-1<<endl;
return 0;
}Example: ants catch a cold
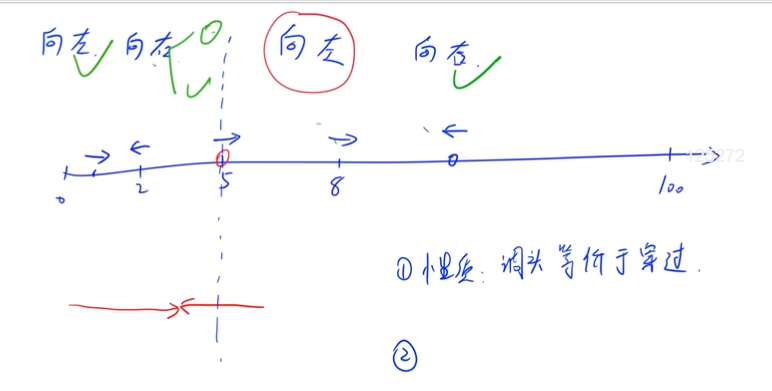
There are # ants on the slender straight pole with a length of # 100 cm.
Some of their heads face left and some face right.
Each ant can only climb forward along the pole at a speed of 1 cm / s.
When two ants meet, they will turn around and crawl in the opposite direction at the same time.
One of these ants caught a cold.
And when they meet other ants, they will infect them with colds.
Please calculate how many ants catch a cold when all the ants climb off the pole.
Input format
In the first line, enter an integer n, which represents the total number of ants.
The next line is n , integer , XiXi separated by spaces. The absolute value of , represents the distance of the ant from the left endpoint of the pole.
A positive value indicates that the head is facing right and a negative value indicates that the head is facing left. The value of 0 will not appear in the data, nor will two ants occupy the same position.
Among them, the first data represents that the ant has a cold.
Output format
Output an integer indicating the number of last cold ants.
Data range
1<n<50
0<|Xi|<100
Input example 1:
3 5 -2 8
Output example 1:
1
Input example 2:
5 -10 8 -20 12 25
Output example 2:
3
Problem solving ideas


Problem solving code
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55;
int n;
int x[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> x[i];//Read all the ants in
int left = 0, right = 0; // It indicates the number of ants walking left and right, and the number of ants walking left on the right
for (int i = 1; i < n; i ++ )
if (abs(x[i]) < abs(x[0]) && x[i] > 0) left ++ ;
else if (abs(x[i]) > abs(x[0]) && x[i] < 0) right ++ ;
if (x[0] > 0 && right == 0 || x[0] < 0 && left == 0) cout << 1 << endl;
else cout << left + right + 1 << endl;
return 0;
}
Example: Beverage exchange
LeYang beverage factory is holding a promotional activity. LeYang type C drink can be replaced with another bottle of type C drink with three bottle caps, and can be recycled all the time (but temporary loan or credit is not allowed).
Please calculate, if Xiao Ming doesn't waste bottle caps and takes part in the activity as much as possible, how many bottles of drinks can he drink in the end for the # bottles of drinks he initially bought.
Input format
Enter an integer n to indicate the number of drinks initially purchased.
Output format
Output an integer indicating the total number of drinks you can drink.
Data range
0<n<10000
Input sample:
100
Output example:
149
Problem solving ideas


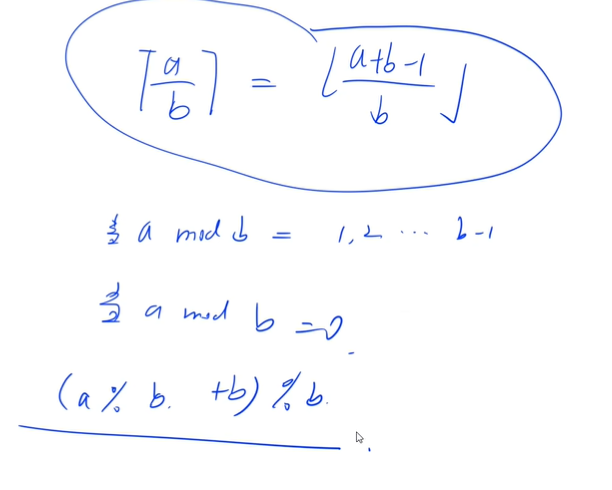
Code problem solving
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int res = n;
while (n >= 3)
{
res += n / 3;
n = n / 3 + n % 3;
}
cout << res << endl;
return 0;
}Simple DP

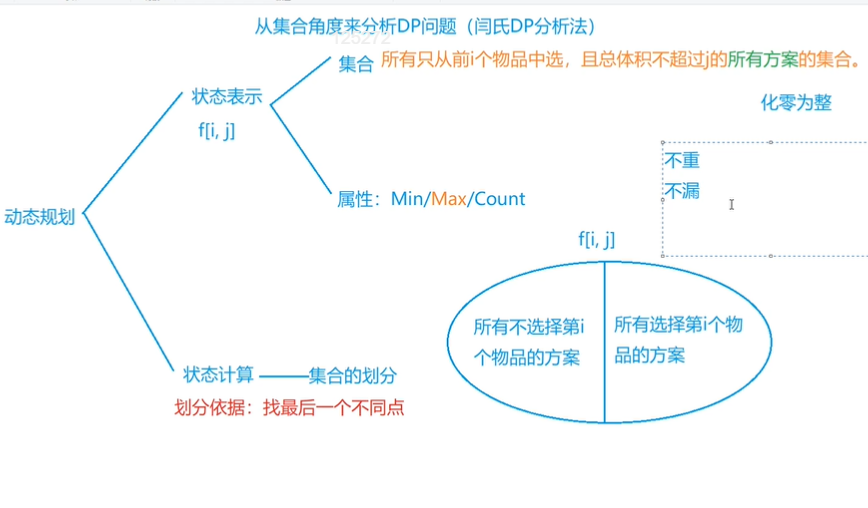
Example: 0-1 knapsack problem
There are # N items and a backpack with a capacity of # V. Each item can only be used once.
The volume of the # i # article is # vi and the value is # wi.
Solve which items are loaded into the backpack, so that the total volume of these items does not exceed the backpack capacity, and the total value is the largest.
Output maximum value.
Input format
In the first line, two integers, N and V, are separated by spaces, representing the number of items and the volume of the backpack respectively.
Next, there are ^ N ^ lines, with two integers ^ VI and WI in each line, separated by spaces, representing the volume and value of the ^ i ^ article respectively.
Output format
Output an integer representing the maximum value.
Data range
0<N,V≤1000
0<vi,wi≤1000
sample input
4 5 1 2 2 4 3 4 4 5
Output example:
8
Problem solving ideas

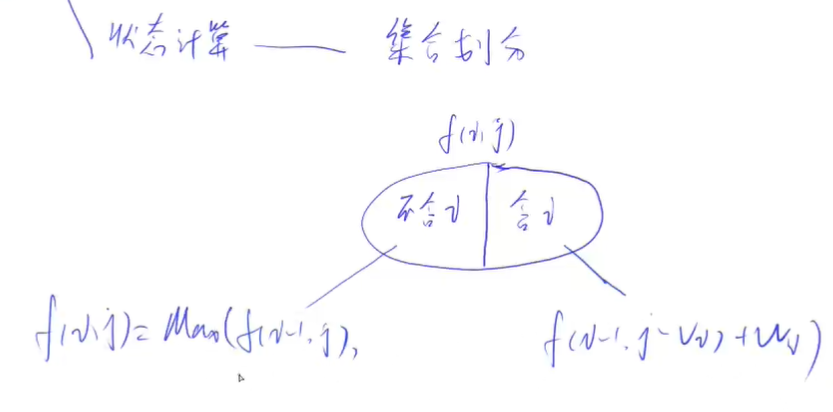
Problem solving code
two-dimensional:
#include <iostream>
#include <algorithm>
using namespace std;
const int N =1010;
int n,m;//n: Number of articles, m: object capacity
int v[N],w[N];//v: Volume, w: value
int f[N][N];//f: Status
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
//f[0][0-m]: Considering 0 items, the total volume shall not exceed 0,1 m. What is the maximum value in this case
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
{
f[i][j]=f[i-1][j];
if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
cout<<f[n][m]<<endl;
return 0;
}one-dimensional:
#include <iostream>
#include <algorithm>
using namespace std;
const int N =1010;
int n,m;//n: Number of articles, m: object capacity
int v[N],w[N];//v: Volume, w: value
int f[N];//f: Status
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
//f[0][0-m]: Considering 0 items, the total volume shall not exceed 0,1 m. What is the maximum value in this case
for(int i=1;i<=n;i++)
for(int j=m;j>=v[i];j--)
f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m]<<endl;
return 0;
}Flower picking
Hello Kitty wants to pick some peanuts for her favorite Mickey Mouse.
She came to a rectangular peanut field with grid roads (as shown below), and went in from the northwest corner and out from the southeast corner.
At the intersection of each road in the field, there is a peanut seedling with several peanuts on it. After a peanut seedling, you can pick all the peanuts on it.
Hello Kitty can only go east or south, not west or North.
Ask Hello Kitty how many peanuts she can pick at most.
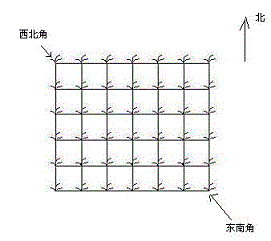
Input format
The first row is an integer T, which represents how many groups of data there are in total.
Next is group T data.
The first row of each group of data is two integers, representing the row number R and column number C of peanut seedlings respectively.
The following R rows of data in each group describe the situation of peanut seedlings in each row from north to south. Each row of data has C integers, which describes the number of peanuts M on each peanut seedling in this row in order from west to East.
Output format
Input data for each group and output a line with the content of the number of peanuts that Hello Kitty can pick the most.
Data range
1≤T≤100
1≤R,C≤100
0≤M≤1000
Input sample:
2 2 2 1 1 3 4 2 3 2 3 4 1 6 5
Output example:
8 16
Problem solving ideas
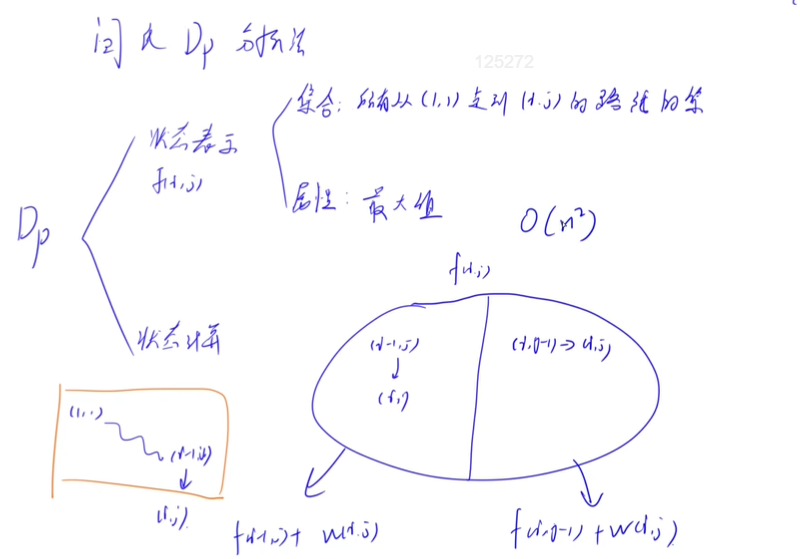
Problem solving code
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int w[N][N];
int f[N][N];
int main()
{
int T;
cin >> T;
while (T -- )
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
cin >> w[i][j];
memset(f, 0, sizeof f);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
cout << f[n][m] << endl;
}
return 0;
}
Example: Longest ascending subsequence
Given a sequence of numbers with a length of , N , find the longest length of the subsequence with strictly monotonically increasing values.
Input format
The first line contains the integer N.
The second line contains N # integers, representing the complete sequence.
Output format
Output an integer representing the maximum length.
Data range
1≤N≤1000
− 10 ^ 9 ≤ number in the sequence ≤ 10 ^ 9
Input sample:
7 3 1 2 1 8 5 6
Output example:
4
Problem solving ideas

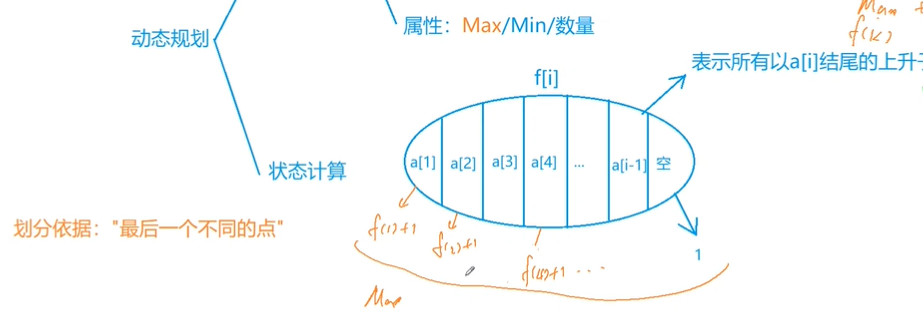
Problem solving code
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ )//Find the value of each fi separately
{
f[i] = 1; // There is only a[i] one number
for (int j = 1; j < i; j ++ )
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);//Maximum value per fi
printf("%d\n", res);
return 0;
}Exercise training
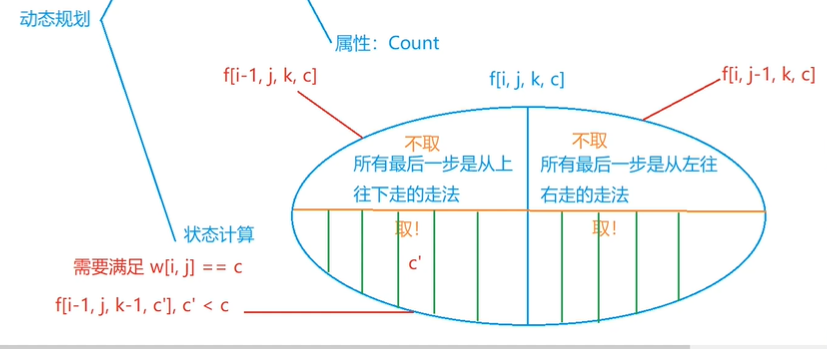
Exercise: Treasure taking in underground palace
King X has an underground palace treasure house, which is n × A matrix of m squares, with one baby in each lattice, and each baby is attached with a value tag.
The entrance of the underground palace is in the upper left corner and the exit is in the lower right corner.
Xiao Ming was taken to the entrance of the underground palace. The king asked him to walk only to the right or down.
When walking through a grid, if the value of the baby in that grid is greater than that of any baby in Xiaoming's hand, Xiaoming can pick it up (of course, he can also not take it).
When Xiaoming comes to the exit, if the baby in his hand happens to be k pieces, these babies can be given to Xiaoming.
Please help Xiao Ming calculate how many different action plans he can get this k# treasure in a given situation.
Input format
In the first line, there are 3 integers, n,m,k. see the title description for the meaning.
Next, there are # n # rows, each of which has # m # integers # Ci # to describe the treasure value of each grid of the treasure matrix.
Output format
Output an integer to indicate the number of action plans for exactly k# babies.
This number may be very large. Output the result of its modulus of # 1000000007.
Data range
1≤n,m≤50
1≤k≤12,
0≤Ci≤12
Input example 1:
2 2 2 1 2 2 1
Output example 1:
2
Input example 2:
2 3 2 1 2 3 2 1 5
Output example 2:
14
Problem solving ideas

Problem solving code
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55, MOD = 1000000007;
int n, m, k;
int w[N][N];//Original value for each location
int f[N][N][13][14];//state
int main()
{
cin >> n >> m >> k;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
cin >> w[i][j];
w[i][j] ++ ;
}
f[1][1][1][w[1][1]] = 1;//Choose the first number
f[1][1][0][0] = 1;//Not selected
for (int i = 1; i <= n; i ++ )//Cycle all States
for (int j = 1; j <= m; j ++ )
{
if (i == 1 && j == 1) continue;//Represents the number of the first upper left corner
for (int u = 0; u <= k; u ++ )
for (int v = 0; v <= 13; v ++ )
{
int &val = f[i][j][u][v];
val = (val + f[i - 1][j][u][v]) % MOD;
val = (val + f[i][j - 1][u][v]) % MOD;
if (u > 0 && v == w[i][j])
{
for (int c = 0; c < v; c ++ )
{
val = (val + f[i - 1][j][u - 1][c]) % MOD;
val = (val + f[i][j - 1][u - 1][c]) % MOD;
}
}
}
}
int res = 0;
for (int i = 0; i <= 13; i ++ ) res = (res + f[n][m][k][i]) % MOD;
cout << res << endl;
return 0;
}
Exercise: wave series
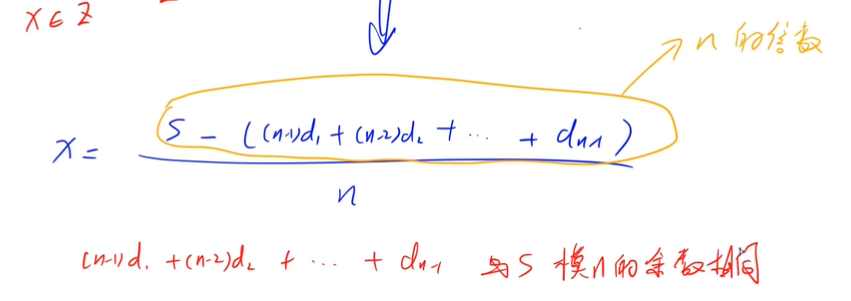
Observe this sequence:
1 3 0 2 -1 1 -2 ...
The latter item in this sequence is always 2 or 3 more or less than the previous item, and each item is an integer.
Dong Dong is very curious about this kind of number series. He wants to know how many kinds of integer number series with lengths of ^ n ^ and ^ s ^ and the latter one always increases ^ a ^ or decreases ^ b ^ compared with the previous one?
Input format
There is one line in total, including four integers , n, s, a and B. the meaning is as described above.
Output format
A total of one line, including an integer, indicating the number of schemes that meet the conditions.
Since this number is very large, please output the remainder of the number of schemes divided by {100000007.
Data range
1≤n≤1000,
−10^9≤s≤10^9
1≤a,b≤10^6
Input sample:
4 10 2 3
Output example:
2
Example explanation
The two sequences satisfying the conditions are 24 1 3 and 7 4 1 - 2 respectively.
Problem solving ideas
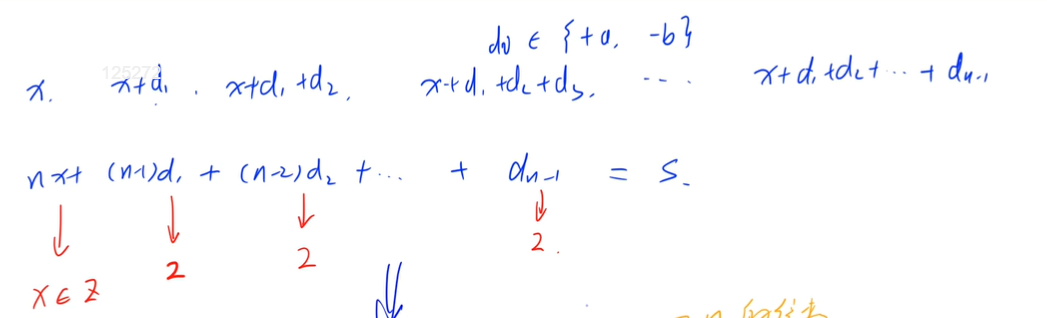
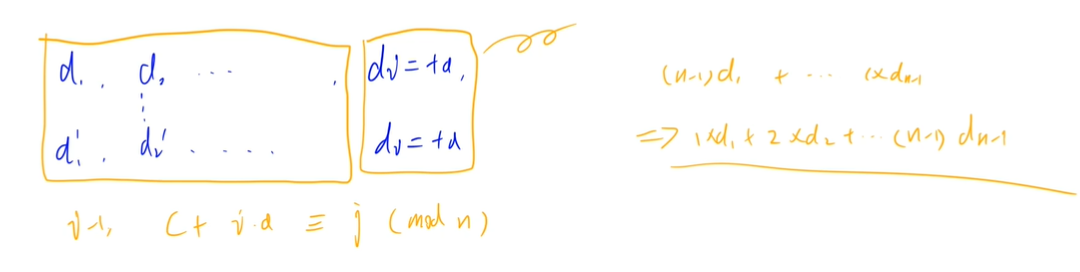
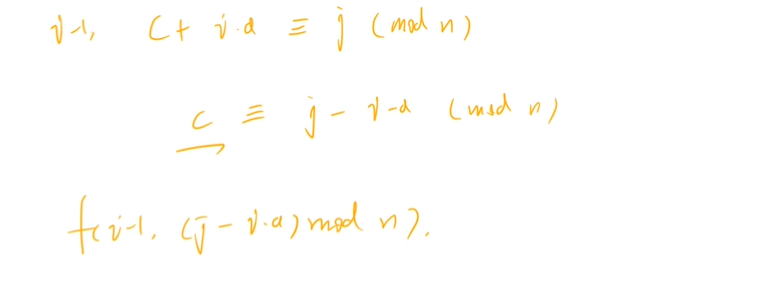
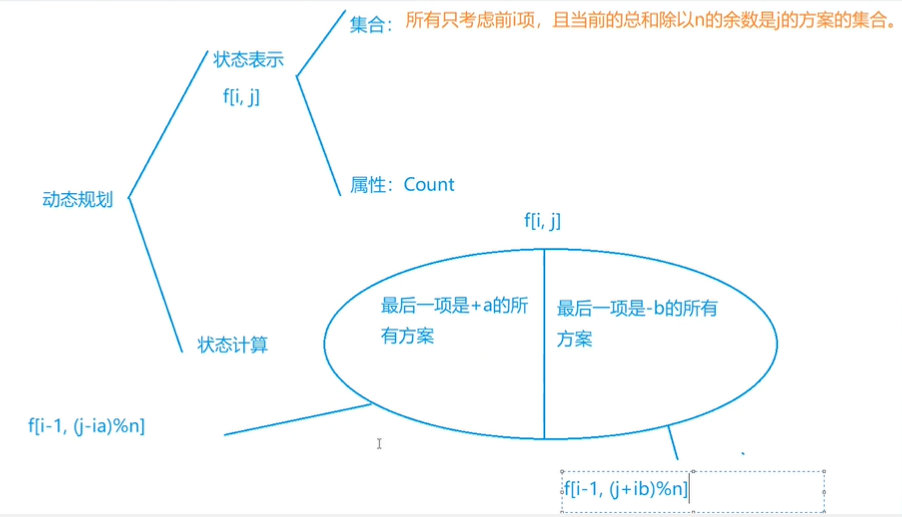
Problem solving code
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, MOD = 100000007;
int f[N][N];
int get_mod(int a, int b) // Find the positive remainder of a divided by b
{
return (a % b + b) % b;
}
int main()
{
int n, s, a, b;
cin >> n >> s >> a >> b;
f[0][0] = 1;
for (int i = 1; i < n; i ++ )
for (int j = 0; j < n; j ++ )
f[i][j] = (f[i - 1][get_mod(j - a * (n - i), n)] + f[i - 1][get_mod(j + b * (n - i), n)]) % MOD;
cout << f[n - 1][get_mod(s, n)] << endl;
return 0;
}