Multi dimensional array in MATLAB refers to an array with more than two dimensions. In a matrix, two dimensions are represented by rows and columns.

Each element is defined by two subscripts, namely row index and column index. A multidimensional array is an extension of a two-dimensional matrix and is indexed with additional subscripts. For example, a three-dimensional array uses three subscripts. The first two dimensions of the matrix are like the number of pages.
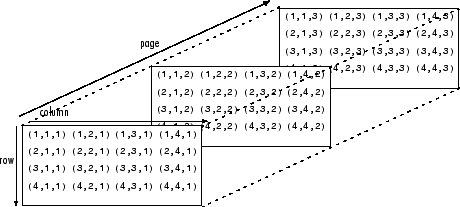
Create multidimensional array
To create a multidimensional array, you can first create a two-dimensional matrix and then expand it. For example, first define a 3 × 3 matrix as the first page in the three-dimensional array.
A = [1 2 3; 4 5 6; 7 8 9] A = 3×3
1 2 3 4 5 6 7 8 9
Now add a second page. To do this, add another 3 × 3 the matrix assigns the index value 2 in the third dimension. Syntax A(:,:,2) uses colons in the first and second dimensions to include all rows and columns to the right of the assignment expression.
A(:,:,2) = [10 11 12; 13 14 15; 16 17 18] A = A(:,:,1) =
1 2 3 4 5 6 7 8 9
A(:,:,2) =
10 11 12 13 14 15 16 17 18
The cat function can be used to construct multidimensional arrays. For example, add A third page in series after A to create A new three-dimensional array B. The first parameter indicates which dimension to concatenate along.
B = cat(3,A,[3 2 1; 0 9 8; 5 3 7]) B = B(:,:,1) =
1 2 3 4 5 6 7 8 9
B(:,:,2) =
10 11 12 13 14 15 16 17 18
B(:,:,3) =
3 2 1 0 9 8 5 3 7
Another way to quickly expand multidimensional arrays is to assign an element to an entire page. For example, add a fourth page to array B, which contains all values of zero.
B(:,:,4) = 0 B = B(:,:,1) =
1 2 3 4 5 6 7 8 9
B(:,:,2) =
10 11 12 13 14 15 16 17 18
B(:,:,3) =
3 2 1 0 9 8 5 3 7
B(:,:,4) =
0 0 0 0 0 0 0 0 0
Access element
To access elements in a multidimensional array, use integer subscripts, just as in vectors and matrices. For example, find the element with subscript 1,2,2 in a, which is located in the first row and second column on the second page of A.
A A = A(:,:,1) =
1 2 3 4 5 6 7 8 9
A(:,:,2) =
10 11 12 13 14 15 16 17 18
elA = A(1,2,2) elA = 11
In the second dimension, the index vector [1,3] is used to access only the first and last columns on each page of A.
C = A(:,[1 3],:) C = C(:,:,1) =
1 3 4 6 7 9
C(:,:,2) =
10 12 13 15 16 18
To find the second and third rows of each page, use the colon operator to create an index vector.
D = A(2:3,:,:) D = D(:,:,1) =
4 5 6 7 8 9
D(:,:,2) =
13 14 15 16 17 18
Operation array
The elements of a multidimensional array can be moved in many ways, similar to vectors and matrices. The reshape, permute, and squeeze functions can be used to rearrange elements. Suppose you have a two page three-dimensional array.
Refactoring multidimensional arrays can help perform certain operations or visualize data. Use the reshape function to rearrange the elements of a three-dimensional array into 6 × 5 matrix.
A = [1 2 3 4 5; 9 0 6 3 7; 8 1 5 0 2]; A(:,:,2) = [9 7 8 5 2; 3 5 8 5 1; 6 9 4 3 3]; B = reshape(A,[6 5]) B = 6×5
1 3 5 7 5 9 6 7 5 5 8 5 2 9 3 2 4 9 8 2 0 3 3 8 1 1 0 6 4 3
reshape operates column by column, extracting elements one by one continuously along the columns in A to create A new matrix, starting from the first page, followed by the second page.
The displacement operation is used to rearrange the dimension order of the array. Suppose there is a three-dimensional array M.
M(:,:,1) = [1 2 3; 4 5 6; 7 8 9]; M(:,:,2) = [0 5 4; 2 7 6; 9 3 1] M = M(:,:,1) =
1 2 3 4 5 6 7 8 9
M(:,:,2) =
0 5 4 2 7 6 9 3 1
Use the permute function to exchange row and column subscripts on each page by specifying the dimension order in the second parameter. The original row of M is now a column, and the original column is now a row.
P1 = permute(M,[2 1 3]) P1 = P1(:,:,1) =
1 4 7 2 5 8 3 6 9
P1(:,:,2) =
0 2 9 5 7 3 4 6 1
Similarly, the row subscript and page subscript of M are exchanged.
P2 = permute(M,[3 2 1]) P2 = P2(:,:,1) =
1 2 3 0 5 4
P2(:,:,2) =
4 5 6 2 7 6
P2(:,:,3) =
7 8 9 9 3 1
When working with multidimensional arrays, you may encounter that some arrays have a redundant dimension with a length of 1. The squeeze function can perform another operation to eliminate a dimension of length 1. For example, use the repmat function to create a 2 × three × one × 4 array, whose elements are all 5, and the length of the third dimension is 1.
A = repmat(5,[2 3 1 4]) A = A(:,:,1,1) =
5 5 5 5 5 5
A(:,:,1,2) =
5 5 5 5 5 5
A(:,:,1,3) =
5 5 5 5 5 5
A(:,:,1,4) =
5 5 5 5 5 5
szA = size(A) szA = 1×4
2 3 1 4
numdimsA = ndims(A) numdimsA = 4
Use the squeeze function to delete the third dimension to get a three-dimensional array.
B = squeeze(A) B = B(:,:,1) =
5 5 5 5 5 5
B(:,:,2) =
5 5 5 5 5 5
B(:,:,3) =
5 5 5 5 5 5
B(:,:,4) =
5 5 5 5 5 5
szB = size(B) szB = 1×3
2 3 4
numdimsB = ndims(B) numdimsB = 3